【大宇宙小故事】48 出軌與背叛

撰文|葉李華
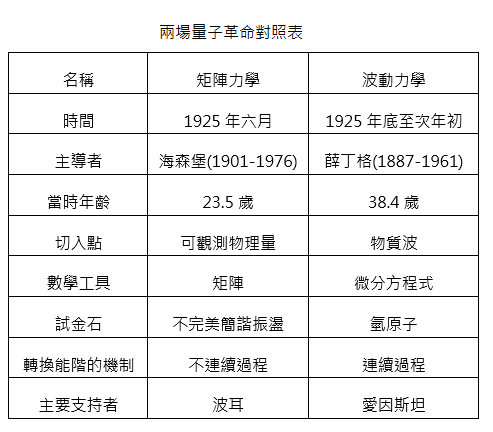
1905是公認的愛因斯坦奇蹟年,不過奇蹟並未立刻降臨在他身上。此後數個寒暑,愛氏繼續待在瑞士伯恩的專利局,直到1909年,蘇黎世大學為他量身打造一個「理論物理教席」,他才獲得第一份正式教職。雖然兩年後愛氏便跳槽,這個教席一直保留下來,曾經有七年的時間(1921-27)由奧地利籍物理學家薛丁格(Erwin Schrödinger, 1887-1961)擔任──這是他們兩人最初的緣分。
1925年11月初,薛丁格讀完德布羅意的博士論文,寫信給愛因斯坦表示贊同,為兩人的第二段緣分揭開序幕。這段時期的史料雖然不完整,而且眾說紛紜,但可以肯定的是,薛丁格當時已經有意完成一項創舉:找出物質波所遵循的方程式。
短短兩個月後,他就有了關鍵性的突破。這同樣要歸功於一次休假,和海森堡的「海姑蘭之夜」頗為類似,不過兩者仍是同中有異:首先薛丁格並非去養病,而是去散心,其次他並非一人獨往,而是有一位神秘女郎為伴。地點是瑞士山區的度假勝地阿羅薩(Arosa),時間是當年年底至次年初。
就某個角度而言,那位神秘女郎在物理發展史上佔有重要地位,可惜無人考據出她的真實身份(主要原因是薛丁格風流成性,檯面上下的情人難以計數)。因此有人打趣說,這也算是「量子不確定性」(Quantum indeterminacy)發揮威力的結果。
耐人尋味的是,薛丁格夫人晚年曾在口述歷史中,堅稱那位女郎就是她自己。她是這麼說的:「他開始研究那個問題的時候,我們正在阿羅薩。我記得就是在那兒,他跟我提到德布羅意和愛因斯坦的論文。」這雖然是一家之言,我們還是應該抱持存而不論的精神,讓這個說法也有機會流傳下去。
交代完這件著名的桃色公案,終於可以進入正題了。
●物理方程式≒物理定律
在探討「薛丁格方程式」之前,有必要先解釋一下方程式在物理學中的角色。大致說來,物理定律與方程式可以畫上等號,如果一定要區分,勉強可說前者是以文字敘述,後者則是一種精煉的數學語言。
因此,一旦寫出某個物理現象的方程式,等於找到描述它的物理定律,剩下的工作「幾乎」就是以數學方法解題而已。這意味著相關的物理內涵盡數藏在那條方程式中,而解方程式的過程就是將物理內涵釋放出來。
舉個最簡單的例子,大家都知道牛頓第二運動定律可以寫成F=ma. 中學的時候,我們將它視為代數方程式,如果力(F)和質量(m)是已知數,加速度(a)就是未知數,答案則是a=F/m. 於是我們得到一個「等加速度」的運動。
然而,如果力的大小或方向不固定,例如會隨著位置變化,F=ma就搖身一變,成了微分方程式。這時它的解不再是某個數值,而是一個函數,例如x(t)=sin(ωt), 其中x是位置,t是時間。
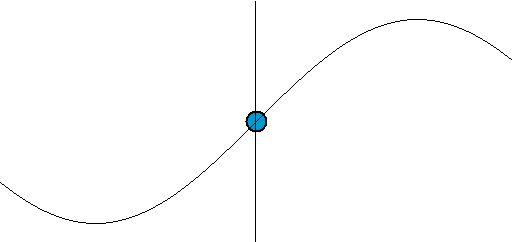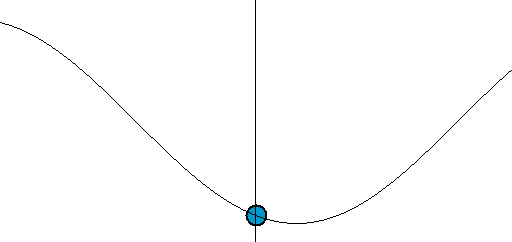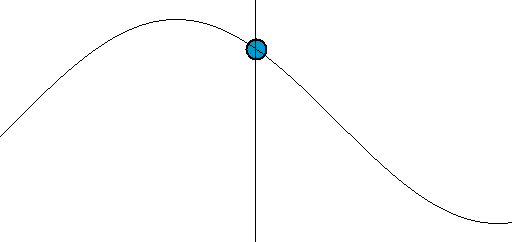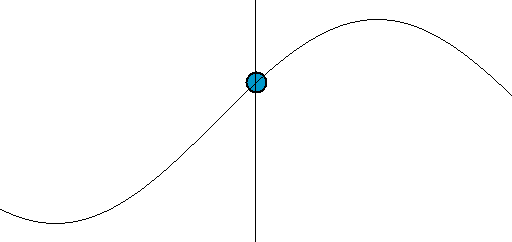
以彈簧的運動為例,一旦寫出彈簧方程式F=-kx=ma(胡克定律+牛頓第二運動定律),彈簧的運動就不再神秘,因為我們不難得到諸如x(t)=sin(ωt)這樣的解。就物理而言,它描述了彈簧(末端)的位置隨著時間變化的方式。
推而廣之,只要把F=ma視為微分方程式,就能用數學方法解決很多力學問題(例如配合萬有引力定律,就能解出行星的位置如何隨著時間變化)。換句話說,F=ma控制了許多力學系統的行為。
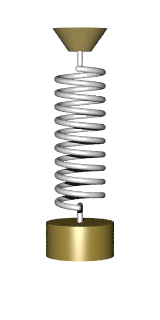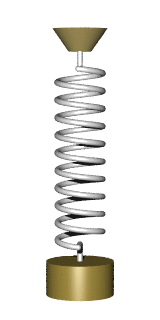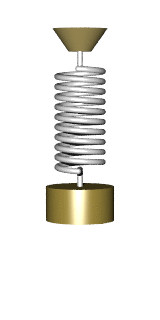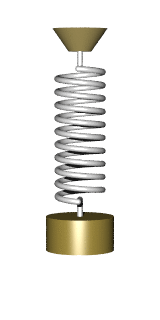
(左)彈簧的運動──簡諧振盪;(右)繩波的行為──
同理,波動方程式則是負責控制波動的行為。由於波動的振幅是位置和時間兩者的函數,所以形式比較複雜,但道理完全一樣。舉例而言,一旦導出(真空中的)電磁波方程式,我們就不難得到諸如E(x, t)=sin(x-ωt)這樣的解。事實上,馬克士威當年正是先導出方程式,才大膽預測電磁波的存在(請參考〈光學終結者〉)。
物質波的情形則是倒過來,德布羅意當初堅信它的存在,卻沒找出它所遵循的方程式,因而無法描述物質波(在各種情況下)的行為。例如在氫原子內,電子的物質波和原子核有強烈的作用,德布羅意只能猜測它的定性行為(一種自我循環的環形波,請參考〈電子波與諾貝爾〉),無法做出更精確的描述。
●波動力學≠物質波的力學
1926年上半年,薛丁格一口氣寫出四篇同名的論文〈量子化視為本徵值問題I~IV〉,詳述了「薛丁格方程式」的推導過程,以及好些重要的應用,就連「波動力學」這個名稱也敲定了。
在第一篇論文中,薛丁格就順利解出氫原子的能階,由此可見(至少就數學而言)他的方法比矩陣力學簡單許多(請參考〈海姑蘭之夜〉)。此外,由於微分方程式是當時物理學家熟悉的工具,波動力學很快便為物理學界接受,愛因斯坦等前輩更是對薛丁格讚譽有加。相較於矩陣力學,兩者最初的際遇可說有著天壤之別。
不過,或許正因為薛丁格方程式十分成功,以致很少有人注意到,在不知不覺間,它的主人已經悄悄自立門戶。這個轉折有點複雜,我們有必要從頭說起。
根據德布羅意的理論,電子兼具微粒性和波動性,只是無法同時觀測到罷了。換言之,電子和它自己的物質波是互補的一體兩面,兩者地位相等,而且永遠形影不離,因此有人將電子波比喻為電子的「影子」。
但是在那四篇同名論文中,頂多只有第一篇勉強反映出「影子波」的概念。從第二篇開始,薛丁格就改變立場,不再承認電子具有彼此互補的兩個面向。千萬別以為他揚棄了電子波,恰恰相反,他認定電子本身是一種「錯覺」,電子波才是真實的物理實體,這正是「波動力學」一詞真正的含意。為了堅定立場,薛丁格甚至改用另一種方法,將方程式重新推導一遍,其思路如下圖所示。
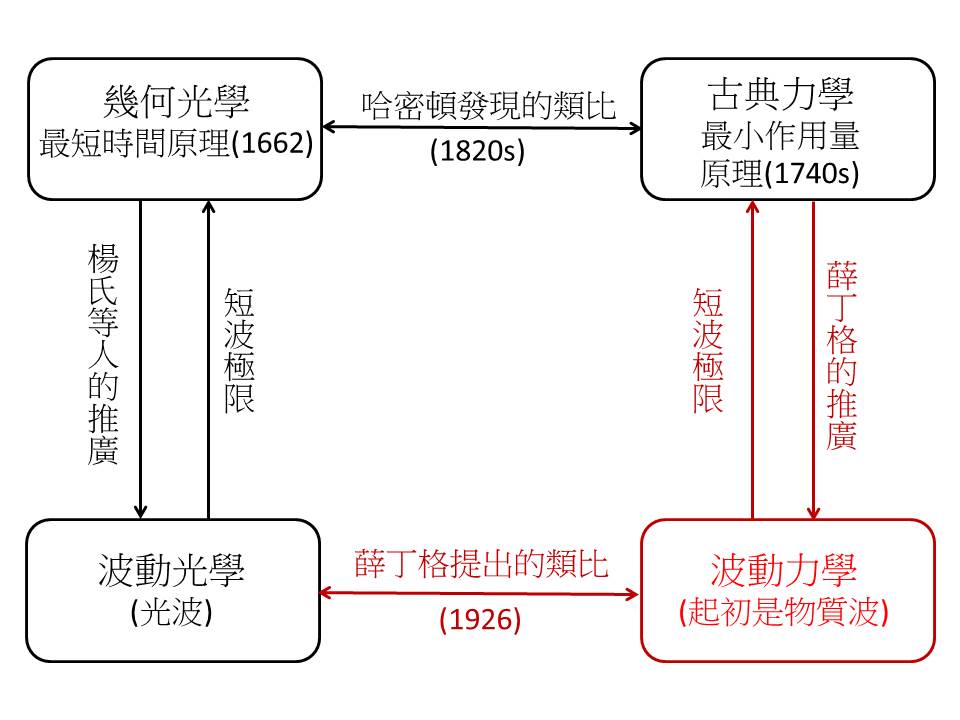
傳統的光學大致分為兩種,所謂的「幾何光學」和「波動光學」,前者將光視為沒有任何結構的「光線」(因此欠缺干涉和繞射),而後者顧名思義以波動說作為理論基礎。這兩種光學並沒有本質上的衝突,因為只要光波的波長夠小,波動光學就會趨近於幾何光學,換言之,幾何光學是波動光學的一種極限。必須強調的是,這裡並未隱含「互補原理」或「波粒二象性」之類的概念,因為「光線」和「微粒」並沒有交集。
另一方面,幾何光學和古典力學之間存在著耐人尋味的類比關係,這是哈密頓(請參考〈從自然數到超複數〉)早年的重要發現。薛丁格則是追尋哈密頓的腳步,為「波動力學」找到適當的定位,然後,在古典力學(以及波動光學)的指導下,他的方程式就呼之欲出了。
因此就本質而言,薛丁格方程式可以算是古典力學的「衍生物」,難怪從它身上還能看到牛頓的影子(並非第二運動定律,而是能量關係式「總能=動能+位能」)。不過請注意,這並不代表我們能用古典力學推導出這條方程式,正如廣義相對論雖然也有牛頓的影子,卻不可能從萬有引力定律嚴格推導出來。
再回到那張圖解,不知大家是否注意到,右下角有「起初是物質波」這幾個字。之所以強調「起初」,是因為在這個類比架構下,薛丁格方程式其實已經和物質波脫鉤!原因正如之前所說,這裡的電子純粹是波動,微粒性只是電子波的短波極限而已,說它是「錯覺」並不為過。既然電子只剩下波動性,薛丁格方程式的解(所謂的「波函數」)當然不能再和物質波的振幅畫上等號──大家不妨想想,德布羅意心中是什麼滋味。
然而,正應了一報還一報這個說法,薛丁格恐怕做夢也想不到,就在他完成第四篇論文的時候,這條方程式也即將背叛它的創造者,不過那當然是另一個故事了。