【大宇宙小故事】25 從自然數到超複數

撰文｜葉李華

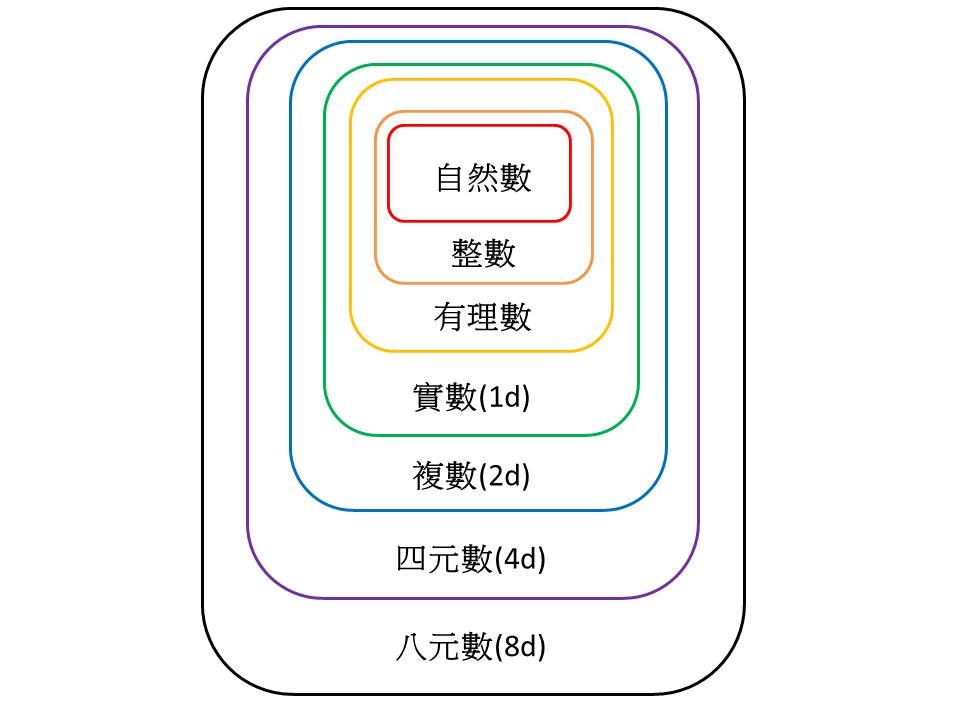
「上帝(僅僅)創造整數，其他都是人類努力的成果。」這是十九世紀德國數學家克氏(L. Kronecker)的名言。然而，如果我們將「上帝」視為「大自然」的同義詞，就必須將「整數」改為「自然數」，唸起來才會比較通順。

事實也的確如此，因為「零」與「負整數」無疑都是人類的發明。例如古代中國並沒有零的概念，所以「零」其實是假借字(原意是零星、零碎)。而「負整數」更不能算是自然界的產物，請問你會不會說「我家院子裡有負三株玫瑰」？

那麼分數呢？這麼說吧，如果你看到切得整整齊齊的半隻雞，會不會以為那是大自然的鬼斧神工？推而廣之，只要扣除自然數，其他的「有理數」通通是數學家的心血結晶。

「無理數」當然更是人工的產物。舉例而言，古希臘的學者經過多年思辨，才終於確定√2是無理數。據說畢氏學派有個學生甚至因此喪命，當然只是謠傳罷了。

然後，想必你還記得「有理數」和「無理數」合稱為「實數」(real number)。這個「實」非常耐人尋味，它表明了自己真實存在於宇宙中。或許我們可以這麼想，只要有空間，就一定有距離；將所有的距離放在一起，就是一組完整的實數了。

換成數學家的說法，則是「直線」和「實數」有一對一的對應關係。因此，如果你畫出一條直線，在上面標示1, 2, 3...這樣的刻度，那麼除了這些(自然數)刻度之外，其他各點所代表的數都跟上帝沒有關係，起碼是沒有直接的關係。

●虛實共構

連中學生都知道，實數之外還有虛數(imaginary number)。當你在解一元二次方程式的時候，虛數已經是不可或缺的工具。

耐人尋味的是，二次方程式的歷史足足有幾千年，虛數卻是十六世紀才出現的，而且當時還不叫「虛數」。在此之前，諸如x²+1=0這樣的方程式都被視為無解。

「實數」和「虛數」這兩個名詞則是十七世紀的產物，兩者都是笛卡兒的發明。在其經典之作《幾何學》(1637)中，笛卡兒頻頻使用「虛數」來指稱負數的平方根，至於「實數」則是伴隨「虛數」而生的名詞，正如「歐氏幾何」之於「非歐幾何」。

從這個「虛」字即可看出笛卡兒自己相當心虛。原因很簡單，這種虛無縹緲、根本不存在於自然界的東西，它在數學、物理以及哲學上到底該如何定位，連笛卡兒這位「近代哲學之父」兼「近代數學之父」也說不清楚。

第一個勉強將它說清楚的人，是大名鼎鼎的數學王子高斯(Carl F. Gauss, 1777-1855)。或許你還記得，所謂的「高斯平面」就是把平面直角座標的橫軸當成實數軸，縱軸當成虛數軸，其中每個點剛好對應一個複數(complex number)，正如同直線和實數有一對一的對應關係。(事實上，高斯並非第一位使用高斯平面的數學家。)

高斯發表相關論文是1831年的事，在此之前，他也曾為「虛數的哲學意義」糾結了三十多年。或許正因為如此，他在論文中特別強調「虛數」是個容易造成誤導的名詞，言下之意大家最好敬而遠之。如果我們用後見之明來評斷，高斯所發明的「複數」在語意上的確比「虛數」優秀許多。

●更上一層樓？

當數學家慢慢接受了虛數和複數之後，自然而然會有人想要更上一層樓，這是數學家的天性。

比方說，既然平面和複數(a+bi)有一對一的對應關係，那麼空間是不是和某種「超複數」(a+bi+cj, 其中j是i的推廣)對應呢？這個問題深深吸引了一位名叫哈密頓(William Hamilton, 1805-1865)的愛爾蘭學者。

哈密頓苦思多年，始終無法找到圓滿的答案。直到1843年底，他走過一座石橋，忽然靈感大發，立刻把頓悟的公式刻在橋上(所以他可算是塗鴉藝術的始祖)。

哈密頓的塗鴉早已磨損殆盡，但如果你現在去都柏林觀光，會看到那座橋上有一塊石板，上面刻著這麼幾句話：

　　1843年10月16日這天

　　當他路過此地

　　哈密頓爵士

　　靈光一閃

　　發覺四元數的乘法

　　服從如下的基本公式

　　i²=j²=k²=ijk=-1

　　順手將它刻在這座橋上

(都柏林市政府忘了加上一句：特殊案例，請勿模仿，否則……)

接下來，當然要解釋一下這個公式背後的意義。

在此之前，哈密頓一直想要建構a+bi+cj這樣的超複數，卻始終無法發明合理的乘法規則。比方說，既然j是i的推廣，i²=j²=-1是理所當然的事，可是ij該等於什麼呢？直到這一天，他才驚覺「更上一層樓」注定是死路，必須一口氣更上兩層樓才行。換句話說，必須將a+bi擴充成a+bi+cj+dk(j, k都是i的推廣)，這樣的數系結構才會擁有合理的乘法。

哈密頓將這個「超複數」命名為「四元數」(quaternion)，這個名詞很容易顧名思義，用不著多做解釋。

或許你會擔心四元數無法和三維空間一一對應，所以沒有幾何意義。其實，想要得到這樣的對應關係，只要把四元數的「實部」定為零就行了。換言之，要對應三維座標，bi+cj+dk是再自然不過的選擇。

四元數有一個特殊性質(可從上面的公式導出來)，那就是i, j, k三者的乘法必須滿足「反交換」關係，例如ij=-ji=k. 如果我們將i, j, k視為矩陣，這種反交換關係其實不難理解。但是當時(1843年)矩陣理論尚未正式誕生，由此可見哈密頓是多麼藝高膽大。

●再上幾層樓？

看到這裡，你會不會開始動腦筋，想把四元數再推廣成更超級的複數？

根據歷史教訓，下一個超複數應該不是五元數，也不太可能是六元數。可是到底是幾元數呢？其實，前面幾個數系的「維度」(基底的數目)提供了很明顯的線索。

從實數到複數，再從複數到四元數，維度的變化是1→2→4, 因此我們可以大膽預言，下一個超複數應該是「八元數」(octonion)。

事實上，在哈密頓發明四元數之後短短兩個月，他的朋友(John Graves)就發明了八元數(主要是找到正確的乘法規則)，但由於論文發表較遲，所以根據正式的數學史，八元數的發明者另有其人(Arthur Cayley)。

至於八元數有些什麼特殊規則，我們可以用歸納法來思考這個問題。

在實數推廣到複數的過程中，「次序」的概念被犧牲了。因為實數具有明確的大小次序(例如2>1>-1)，而複數卻沒有(你不能說2+i>1+i, 也不能說2+i<1+i)。

複數推廣到四元數的過程中又犧牲了什麼呢？其實剛才已經提到，犧牲了「乘法的交換律」。

那麼，當我們將四元數推廣到八元數，還能再犧牲什麼呢？那就是或許比「交換律」更基本的「結合律」。

所以說，八元數最大的特色就是連乘法的結合律都不見了。如果你想讓三個八元數x, y, z依照這個順序相乘，寫成xyz根本沒有意義，必須寫成(xy)z或是x(yz)，前者代表先進行xy的乘法，後者則以此類推。

前面提到，只要你熟悉矩陣，就不至於對「非交換性」太過陌生。換成數學的說法，就是四元數的i, j, k都可以用矩陣來表現，所以a+bi+cj+dk其實就是四個矩陣相加，結果當然還是一個矩陣，並沒有什麼神秘的。

但由於矩陣乘法服從結合律，而八元數並不服從，這意味著你根本不能用矩陣來表現八元數，因此就連數學家都對它有點頭痛。

●到了盡頭？

如果你想再接再厲，將八元數擴充為十六元數，那麼根據上述的「犧牲規律」，你得先找出還有什麼能犧牲的。可是不論你多麼努力，恐怕都是徒勞無功。這就代表八元數的犧牲已經到了盡頭，所以它就是最高維的超複數。

這是個很重要的數學定理，它有個可愛的暱稱「1,2,4,8定理」。

然而，這是否代表超複數的演化真的到了盡頭？答案則是見仁見智。因為上述的四元數與八元數只能算是超複數的一種「正統」類型，我們若對血統的純正稍微放鬆一點，就能另闢蹊徑，發明出更多的超複數，不過那當然是另一個故事了。

註一：何謂正統？

複數z=a+bi的絕對值平方=|z|²=zz*=(a+bi)(a-bi)=a²+b².

若z, w皆為複數，那麼|z|²|w|²=zz*ww*=zwz*w*=(zw)(zw)*=|zw|².

因此我們得到|z||w|=|zw|這個關係。

將z, w推廣成四元數，雖然乘法沒有交換律，我們能夠證明|z||w|=|zw|仍舊成立。

將z, w推廣成八元數，雖然乘法沒有交換律和結合律，|z||w|=|zw|同樣成立。

所以服從|z||w|=|zw|的數系就是我們所謂的正統數系(數學家當然另有名稱)。

註二：若用實係數來展開，那麼對於複數而言，|z|²|w|²=|zw|²這個關係對應於Fibonacci恆等式(能寫成平方和的兩個整數相乘，結果仍能寫成平方和)：(a²+b²)(c²+d²)=(ac+bd)²+(ad-bc)²=(ac-bd)²+(ad+bc)².

推而廣之，四元數所對應的關係式為Euler四平方和恆等式，而八元數對應的關係式則是Degen八平方和恆等式。根據「1,2,4,8定理」，這類的關係式到此為止，千萬別不信邪，白白浪費時間！