微積分的dx(一)：無限小數與非標準分析學

17世紀時牛頓和萊布尼茲發明了微積分。其中萊布尼茲的「積分符號」∫、「極微小差」dx 等兩個符號仍然使用至今。現今的課本會用「極限」解釋，所以有些人說 dx 只是符號，不需要實質意義。這兩種觀點都有其意義和重要性。本文將分為若干期，從不同觀點探索微積分的靈魂、以及各觀點的應用。

撰文｜李龍欣

●為何有微積分

自古以來，數學家們就深知自然萬物難以測量，而不如圓形、多邊形、橢圓一般簡潔。我們固然可以拿起一把尺開始耐著性子量，例如阿基米德 (Αρχιμήδης ο Συρακούσιος)、劉徽、關孝和 (関 孝和) 的割圓術，又譬如古巴比倫人的三角函數表，都是測量的典範和先驅。雖然以人類的力量和壽命，必定會留下誤差，但是只要我們願意再量幾次，就可以把誤差一直縮小。所以理想上的誤差是「無限小的數 (infinitesimal number)」，與無限大相對。17世紀，勒內．笛卡兒 (René Descartes) 發明解析幾何，再次帶動了無限小數的討論。這門學問被稱做「分析學 (analysis)」或「數學分析 (mathematical analysis)」。終於在同一世紀，艾薩克．牛頓 (Isaac Newton)、哥特佛萊德．萊布尼茲 (Gottfried Leibniz) 確立了分析學的基礎。所以他們被尊為微積分的發明者^註1。

●無限大與無限小

「無限」的概念太難描繪，但也因此而迷人。「無限大」是什麼呢？無限大減一是什麼？無限大減無限大是什麼？「無限大」已經夠難了，「無限小」卻更難。我們或許能想像在數線看不到的地方有個盡頭，那裡的數字叫做無限大。無限小卻是硬生生地在我們眼前消失。無限小在數線的位置應該和 0 一模一樣，可是無限小又不是 0！

●超實數

微積分發明之初，仍是以無限小描述，因此十分難以理解。到了19世紀初，從萊布尼茲的理論中發展出了「極限 (limit)」的概念。此舉推翻了過往的討論，捨棄了無限小的想法。同一世紀，邏輯學發展起來之後，追求嚴謹的浪潮更讓無限小被打入冷宮。

直到1960年代，亞伯拉罕．魯賓遜 (Abraham Robinson) 運用邏輯學證明^註2可以把實數「擴充」而不產生任何矛盾。相對於已經普及的極限理論，浴火重生的無限小理論被稱為「非標準分析學 (nonstandard analysis)」。魯賓遜以 R 代表實數 (real numbers)，*R 表示擴充後的實數，又稱為超實數 (hyperreal numbers)。凡是在 R 成立的一階邏輯 (first order logic) 命題，在 *R 也會成立。例如：

．具有四則運算。(任兩數可相加、減、乘，若第二個數不是 0 可以相除)

．任兩數能比大小，且正數的加法、乘法保持大小關係。

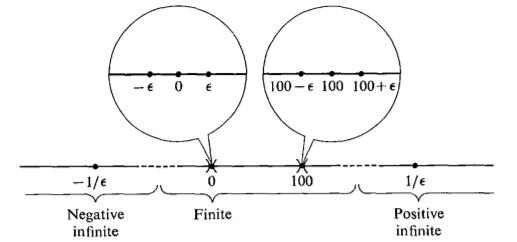
在 *R 中，比所有實數都大的數^註3，是正無限大；比所有實數都小的數，是負無限大；介於兩個實數之間的數，是有限數(包含無限小數)；比所有正實數都小又比所有負實數都大的數^註3，是無限小(包含 0)。直覺上沒有什麼矛盾的運算規則大概都會成立，例如：

．[正無限大 加 正無限大] 是 正無限大

．[有限 除以 無限大] 是 無限小

在牛頓、萊布尼茲的理論中，都有把無限小數省略的步驟。在 *R 中可以用這個定理解釋：

．任何有限數 x 都能唯一地分成一個實數和一個無限小數的和。其中的實數記為 st(x)，稱為 x 的標準部分 (standard part)。

至於連續函數、微分、積分可以如此定義：^註4

．若 st(x)=c 則有 st(f(x))=f(c)，則稱 f(x) 在 c 連續。

．給定無限小數 dx≠0，f(x) 在 x=c 的微分定為 (若結果跟我們所選的 dx 無關則可微分)

．ω 為無限大整數^註5，a=x₀<ξ₁<x₁<ξ₂<x₂<...<x_ω-1<ξ_ω<x_ω=b 使得 st(x_n-x_n-1)=0，則 f(x) 在 [a,b] 的積分定為^註6 (連續函數都可積分)

魯賓遜以此重新詮釋了很多既有的結果，可說是只要跟實數有關的學科都被涵蓋到了。

●發展

這項成就無非提供了一個有趣的觀點，故也有擁護者，其中更有人把理論部分稍微簡化。只不過批評自然是少不了，例如：使用了選擇公理、邏輯學太深奧、無法構造等等。而數學的發展從來不是為了消弭不同觀點之間的鴻溝，而是要運用各種觀點來解決問題。

 

註解:

[1] 後來二人為此互相指控剽竊，可參考＜誰是受害者＞。
[2] 需要承認選擇公理。
[3] 需注意無限大不是一個數。這種數有很多(無限多個)。無限小也是。
[4] 在前兩條中，f(x) 為開區間 (a,b) 上的函數；後一條則在閉區間 [a,b] 上；a<c<b 為三個不同的實數。
[5] 為正整數的擴充，可參見參考資料[4]，第3章第8節。
[6] 將「加總」的動作視為一個函數，然後將此函數擴充到無限大。

參考資料：

[1] 《A History of Mathematics》。F. Cajori 著。第二版(1961)。Macmillan 出版(紐約)。
[2] 《Non-Standard Analysis》。A. Robinson 著。初版(1966)。North-Holland 出版(阿姆斯特丹)。
[3] 《Lectures on the Hyperreals: An Introduction to Nonstandard Analysis》。R. Goldblatt 著。初版(1998)。Springer-Verlag 出版(紐約/柏林/海德堡)。
[4] 《Elementary Calculus: An Infinitesimal Approach》。H. Keisler 著。2019年9月修訂版。於網路免費公開。網址：http://www.math.wisc.edu/~keisler/calc.html。另有印刷版：第三版(2012)。Dover 出版(紐約)。