【大宇宙小故事】18 無用之用
撰文|葉李華
提洛島是愛琴海中的一個島嶼,面積並不大,卻在古希臘文明中佔有重要地位。傳說公元前四世紀,該島爆發一場大瘟疫,島民為了消災,趕忙請示太陽神阿波羅,得到的神諭是:將神殿裡的正立方祭壇加倍。不料完工後,島上瘟疫依然不止。敢情是島民誤解了神諭的意思,將祭壇的長寬高分別延長為兩倍,使得體積變成原來的八倍。
由於無人知曉該如何建造體積剛好是兩倍的正立方體,他們只好派人前往雅典,求助於當時最有名的學者柏拉圖。
接下來就是比較可信的事蹟,不久之後,柏拉圖的再傳弟子梅氏(Menaechmus)想出一個巧妙的解法,能將任意長度a延伸成∛2a。這個解法在數學上完全正確,就建築學而言也實際可行,偏偏柏拉圖很不滿意,認為梅氏簡直是有辱師門。
問題到底出在哪裡呢?
●圓錐曲線的誕生
根據古希臘數學的傳統,凡是這種幾何作圖題,一律只能使用兩種工具──圓規和沒有刻度的直尺,換言之,只能使用「圓和直線」來解決這類問題。梅氏的方法則要用到拋物線,因此在太師父看來,當然與作弊無異。
但如果拋開柏拉圖的感受不談,梅氏的方法其實是數學史上的重要里程碑。
在現代數學中,拋物線這類「二次曲線」屬於解析幾何的範疇,想必大家在中學都學過。可是別忘了,解析幾何正式出現是十七世紀的事,距離柏拉圖足足有兩千年之久。
因此,雖然我們不妨借用解析幾何來解釋梅氏的方法,但請記住這是個「穿越時空」的折衷方案。
梅氏的方法如下:如果祭壇原來的邊長等於a,我們只要畫出兩條拋物線,方程式分別為x2=ay, y2=2ax, 很容易證明兩者除了相交於原點,還有一個交點是x=∛2a, y=∛4a, 因此第二個交點的x座標值就是答案。
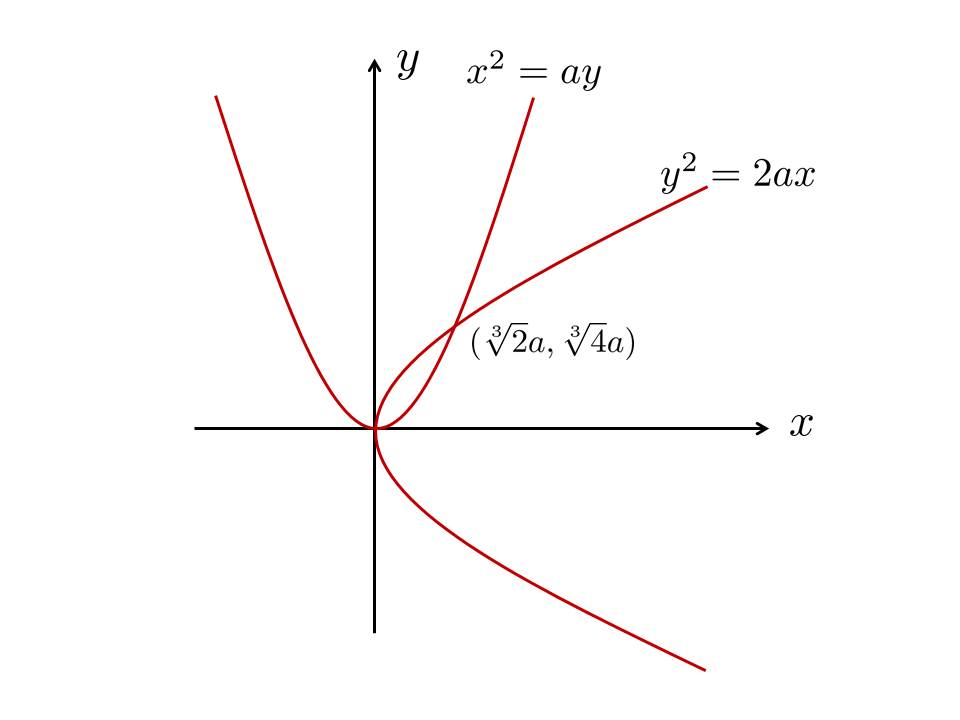
此外梅氏還發現,如果用雙曲線xy=2a2取代上述任何一條拋物線,也能得到正確的結果。但由於古希臘人沒有現代座標的概念,梅氏必須用比較辛苦的方式進行計算,在此就不詳述了。
另一方面,梅氏製造拋物線和雙曲線的方法不但很有創意,而且相當直觀,值得好好介紹一番。
在介紹這個方法之前,先講一個關於創意的小故事:時間大約是1513年,米開朗基羅看到一塊大理石,立刻喊道:「摩西在裡面,我要把他釋放出來!」不久之後,他就完成著名的「摩西像」。這尊雕像雖說是藝術瑰寶,卻有個相當違和之處:摩西竟然長了一對犄角!追根究柢,問題出在拉丁文《聖經》翻譯品質不佳,摩西頭上應該是有幾道光芒才對。
回到正題。梅氏和米開朗基羅一樣獨具慧眼,在平平凡凡的圓錐中,居然看到藏著拋物線和雙曲線。「釋放」的方法則很簡單,只要用一把薄刃的利刀,以不同的角度切開圓錐,形成的「切痕」就不外是拋物線、雙曲線或橢圓這三種曲線(正圓則視為橢圓的特例,以下皆同)。
不過,梅氏或許有點偏執,堅持要用胖瘦不同的三種圓錐,分別切出橢圓、拋物線和雙曲線。如今我們常見的切法,則是一百多年後另一位數學家阿氏(Apollonius of Perga)所提倡的,亦即使用同一個圓錐,切出上述三種不同的曲線。
因此之故,這三種曲線至今仍統稱為圓錐曲線。當然,若要得到完整的雙曲線,一個圓錐絕對不夠,需要兩個圓錐「疊羅漢」才行。
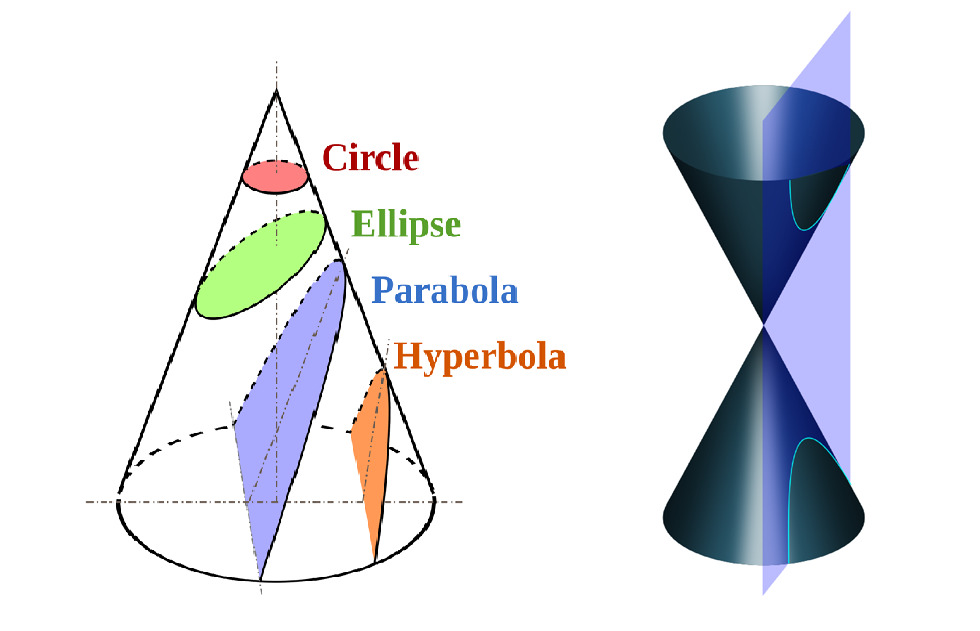
(圖像來源:維基百科)
●暗藏玄機的名字
拋物線、雙曲線、橢圓這三個中文名詞並沒有任何脈絡。或許正因為如此,造成初學者不少困擾。「拋物線」這個譯名可以顧名思義;「雙曲線」則是數學專有名詞,其中的「雙」是強調它有兩段;而「橢圓」最簡單,早已成為日常生活的詞彙。
另一方面,這三種曲線的英文則很有邏輯:拋物線(parabola)、雙曲線(hyperbola)、橢圓(ellipse)分別意味著「平起平坐」、「超過」、「不及」(希臘文源頭的意義則稍有不同)。如果我們用「切出拋物線的角度」當作基準,那麼雙曲線和橢圓就對應於刀面的角度「超過」和「不及」那個基準。因此不妨將這三種曲線翻譯成「恰好曲線」、「超過曲線」和「不及曲線」,或是更文雅的「滿曲線」、「盈曲線」和「虧曲線」。
就這個觀點而言,拋物線剛好介於雙曲線和橢圓之間,正如同零剛好介於正數和負數之間。所以拋物線在某些方面類似橢圓(只有一段),某些性質又類似雙曲線(延伸到無限遠)。若用伊索寓言來比喻,它就是動物界的蝙蝠。
●有用無用?
再講個故事,有個年輕學子請教歐幾里得一個問題:幾何到底有什麼用?歐氏立刻板起臉孔答道:既然你要求回報,我給你一個銅板吧!(接下來的情節大可自行想像。)
不管這個故事是真是假,都說明了古希臘學者對數學的態度是「為研究而研究」,並不關心研究成果是否有實際應用。阿氏自然不例外,他對圓錐曲線做了十分完整的探討,最後寫成一本專書,卻隻字未提圓錐曲線的應用價值。
然而在科學發展史上,經常會出現一種耐人尋味的情形:當時機成熟時,純數學就會走出象牙塔,成為科學家研究自然現象(甚至社會現象)的有力工具。
最現成的例子,就是圓錐曲線在天文學上的應用。例如克卜勒在十七世紀初,根據大量的觀測數據,大膽推測行星軌道都是橢圓(亦即所謂的克卜勒第一定律)。七十多年後,當牛頓撰寫《自然哲學的數學原理》時,發現阿氏早就為他準備好了幾何工具。換句話說,牛頓是站在阿氏肩上證明出下列事實:太陽系的天體軌道一定是圓錐曲線;橢圓軌道對應於行星和週期彗星,拋物線和雙曲線則對應非週期彗星。
從此以後,類似的情節在科學史上不斷上演,直到如今。
●意外副產品
回顧圓錐曲線的歷史,相信大家應該同意,它可說是歐氏幾何的意外副產品。
在歐氏幾何中,作圖題只能使用圓規與直尺,因此留下所謂的「三大難題」(請參考〈歐幾里得故事集〉),開頭提到的「加倍立方體體積」就是其中之一。梅氏不按牌理出牌,用犯規的方法得到解答,雖然不被當時學界認可,卻因而開啟了圓錐曲線的研究。
由此可見,難題正是數學發展的最佳催化劑。即使難題本身暫時無解,它所催化的結果可能早已開枝散葉,甚至造福人群。
不過,我們還是應該關心一下,後來有沒有人找出「加倍立方體體積」的正確解答。
結果或許有點反高潮,公元1837年,法國數學家汪氏(Pierre Wantzel)證明了僅用圓規和直尺絕對無法解決這個問題。然而,負面結果並未折損這道難題的歷史地位,好歹它催生出了圓錐曲線理論。在數學中,至少就知名度而言,圓錐曲線遠勝於三大難題的任何一題。
有趣的是,圓錐曲線本身也有意外的副產品──用來當作分類的工具。剛才說過,三種圓錐曲線可以翻譯成「恰好曲線」、「超過曲線」和「不及曲線」,所以「拋物」、「雙曲」、「橢圓」這三個形容詞很適合用於三分法。
舉例來說,在一八七零年代,非歐幾何蓬勃發展之際,德國數學家克萊因(Felix Klein)就曾提倡將兩種非歐幾何稱為「雙曲幾何」與「橢圓幾何」,而將歐氏幾何改名為「拋物幾何」。
克萊因的倡議成功了三分之二,因為「雙曲幾何」與「橢圓幾何」早已是標準的數學名詞。這兩種非歐幾何也服從上述的歷史規律,當時機成熟時,它們走出象牙塔,成為科學家研究宇宙結構的有力工具。不久之後,我們就會好好討論這段歷史。
註一:十九世紀時,三大難題陸續被證明為不可能,其中「三等分任意角」與「加倍立方體體積」的證明出自同一篇論文,另一題「根據圓面積畫一個正方形」的負面結果則是林氏(Ferdinand von Lindemann)1882年研究圓周率的副產品。
註二:嚴格說來,克萊因是根據「射影幾何」理論,讓拋物線、雙曲線、橢圓分別對應1, 2, 0這三個數,藉以呼應「拋物幾何對應一條平行線」、「雙曲幾何對應(至少)兩條平行線」以及「橢圓幾何對應零條平行線」。
註三:拋物線(parabola)、雙曲線(hyperbola)、橢圓(ellipse)這三個名詞的源頭是阿氏以古希臘文寫成的《圓錐曲線》,他所用的「造字規則」其實和圓錐切痕無關,但由於牽涉到太瑣碎的細節,在此只能表過就算。
