【回音谷】思考「數學與文明—概述與重訪」

■ 人類丈量天空的大夢如何與數學和文明有關？項武義教授今年三月在台大的演講「數學與文明—概述與重訪」引起了這篇迴響。

?撰文 ∣ 施博仁（台大電機系二年級）

　　項武義教授1959年畢業於台大數學系，早年致力於幾何學研究。1990年後反璞歸真，改為研究古典幾何、出版了幾本基礎數學教材，也留意數學、天文學發展史。這段時期，他曾提出了著名的刻卜勒猜想（Kepler’s Conjecture）的證明[註1]，轟動數學界。?

　　3月26日項教授應台大科教中心之邀，以「數學與文明—概述與重訪」為題赴台大舉行演講。此次演說的三大主軸分別是物理學、幾何學、天文學，以大歷史的角度重訪其發展，並認為這三個學科的發展都曾誤入歧途，又迷途知返。就幾何學來說，畢達哥拉斯學派（The Pythagorean School）[註2]相信任何的量都可以表示成簡單的整數比，在幾何學上的意義即是宣稱：給定兩個線段，我們都可以找到一個最長的第三個線段（稱為最大可公度），使這兩個線段都是第三個線段的整數倍。以2cm和2.5cm為例，最大可公度即是0.5cm。然而畢氏學派的美夢破碎了，傳說一位成員Hippasus洩漏（另一說是發現）了不可公度性的秘密[註3]，使學派名聲掃地，驚恐不已的其他成員將他拋進了大海。一直到了Eudoxus（約410 - 355 BC）才解決了幾何學面臨垮台的難題，相關的部份記載於歐幾里德（Euclid）《幾何原本》（Euclid's Elements）第五章（Book V）。

　　然而畢氏學派的錯誤瑕不掩瑜，項武義教授相當肯定畢氏學派的貢獻。畢氏學派宣稱宇宙的和諧和精要在於數、比值和幾何形體的妥加配合，項教授個人認為以今日的後見之明，即是預取了：「數理分析乃是認知大自然的不二法門。」也可以說，相信大自然現象存在著「簡單的」數值關聯，乃是物理學早期發展的關鍵。這點將在稍後闡述。

　　天文學也同樣迷途知返，演講中舉了托勒密（Ptolemy）的地心說（地球中心說）。直到文藝復興時期，哥白尼、伽利略、刻卜勒等天文學家才正式打破這樣有限的宇宙觀。項教授相當推崇刻卜勒（Johannes Kepler,1571-1630），然而平心而論，刻卜勒不過是憑藉著另一個偉大的天文學家第谷（Tycho Brahe, 1546-1601）詳盡的觀察資料，做類似今日我們以excel尋找實驗數據關係的工作。刻卜勒花費了16年，發現行星公轉週期的平方和公轉半徑的立方成正比；這樣的關聯並不直觀，刻卜勒的工作顯然有盲試的成份。

　　或許是因為刻卜勒的信仰，例如相信宇宙是上帝的形象，始終深信星體之間有簡單的幾何、數學關聯，因而不計成本發覺「真理」。即使到了牛頓也不例外，他的著作有極大的部份充滿神學，終其一生力圖以嚴謹的數學方法，證明自然世界中的秩序是上帝的傑作、神的意志活動確實存在。著名經濟學家凱因斯（John Keynes）曾鑽研牛頓遺留的手稿，即認為「牛頓不是理性時代的第一人；他是最後一個煉金術士（magician）」。所以我們千萬不能認為科學始終是一種純粹的理性活動，不如說它深刻反應了科學家的意識觀。

　　或許我們可以說，由於科學革命早期的科學家們，對於精簡關係有相當的信仰，這宇宙也剛好有近似簡單的（整數關係的）法則，才獲致第一場科學發展史上前所未有的大豐收，餘波所及，甚至開啟了啟蒙時代，天真地以為透過經驗、歸納等科學方法，可以完美地為各種人事關聯找出規律、法則。然而我們必須指出，天體的運動機制其實太過簡單，不過是萬有引力定律，而且因為理論上，球體間的引力可以等效將質量全部集中於球心而大為簡輕了問題的複雜度，加上真空中沒有阻力、其他星系對於太陽系引力干涉不足以混淆視聽。

　　有趣的是，1846年英國與法國兩位天文數學家勒維耶（Urbain Le Verrier）與亞歷斯‧布瓦（Alexis Bouvard）分別由天王星的攝動現象計算出海王星的軌道。在天文學史上，是一件了不得的大事，同時也是少數天才才能夠憑著紙筆計算完成的艱難創舉。當時參與其中的巴黎天文台台長François Arago稱「在筆頭的尖端看見了這顆行星」並不為過。然而當代作者Michael Hoskin在著名的《劍橋插圖天文史》意味深長地評論道：「對海王星的發現是牛頓力學成功的巔峰。」因為當時的天文學家將發現的海王星考慮進去之後，重新計算水星的近日點，卻發現每一世紀比理論算出的多了38弧秒（1弧秒 = 1/3600度）。勒維耶又用了同樣的方法，認為水星軌道內還有另一顆行星，這次他卻錯了。直到1915年愛因斯坦發表了廣義相對論之後，闡明萬有引力定律只是一個近似的關係，才完整解決了水星的問題。

　　在此，值得大家思考的是，「不多不少的」誤差允許了牛頓以來的人憑著有限的測量工具印證簡單的數學關係，物理科學才得以發展。

　　其實，在科學發展史上迷途知返的歷程屢見不鮮，甚至是必經的程序、必然的事實。科學史家孔恩（Thomas Kuhn）對於科學史的研究就指出，科學的演進不是新知識的線性累積（linear accumulation），而是一場一場週期性的革命（periodic revolutions）：一批新的科學家打破舊有的「法則」，科學的典範（paradigm）面臨危機，當新的、異常的證據逐漸建立出來後，舊有的法則連同新的研究，形成一個更大而兼容的體系（framework），他的科學史研究指出科學的發展也有革命的色彩。

　　即便是最接近純粹理性的數學也如此。根據哲學史的記載，項教授推崇的畢氏學派就帶有神秘主義的思想色彩。畢氏學派即以數字1為理性、2為俗見、5為結婚、6為靈魂，足以見得他們的數學成就同時反映他們的宗教觀。從前的哲學家可謂名副其實的愛智者（Philosophy），直到牛頓都還有這樣的傾向。他們無所不究，仰觀天文俯察地理、猜度宇宙的起源以及物質的組成都是他們的興趣。

　　回過頭來，喜歡數學的人或許仍堅稱數式之間嚴謹的推理，乃是最接近純粹理性的學科，因為它只憑藉著一些公設（axioms），即可浩浩蕩蕩展開構思嚴密且蔚然可觀的版圖。然而，這些公設相當直觀，數學發展史上早期的根基可謂由經驗、宇宙觀甚至宗教觀而來。現今大多學習數學的人（除了數學系學生以外）則已經甚少鑽研公設的正確性，或是各種直觀的衍生定理如何由公設一步一步推導——這是一個一般人望之卻步的煩冗驗證工作。數學就如人文學、社會科學，也逃不過積累性學科的範疇，必有部份因襲前人的成果而不再詳加檢驗。所以與其說大多數擅長數學的人，對於數學的敏銳度乃是一種理性的洞見，不如說只是仰仗基本的直觀與表象的經驗而已。

　　所以科學革命時期的科學家過於天真；以為瞭解數學即是接近真理的人，卻可能與真理失之交臂。在這個科技、科學成果已洋洋可觀的時代中，科學家與數學家千萬不能沾沾自喜。對於真理是什麼、還有誰能執起摩西的杖（Moses' rod）引領人類安然度過21世紀。項教授帶領我們重訪的歷史告訴我們，應抱持謙卑、誠敬的心面對所有未知的一切。

　　根據可信的資料，項武義教授1992、1993年提出刻卜勒猜想的證明，在1994年就被駁斥，著名的數學百科全書MathWorld引用J. H. Conway說這個證明的有效性：“ it is nonsense.”，甚至一些文獻上有負面的評述[註4]。然而放在整個數學、科學發展脈絡來看，挑戰失敗的人太多了[5]。項教授在演講中提到自己仍在著手翻修這個證明，且讓我們拭目以待！

?

---

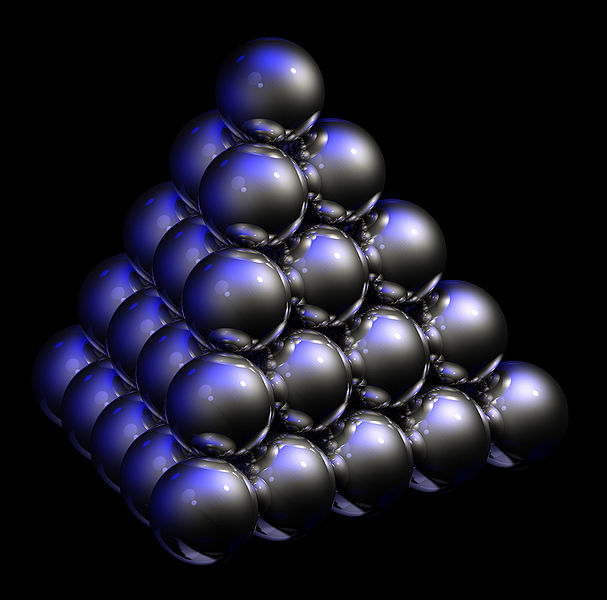
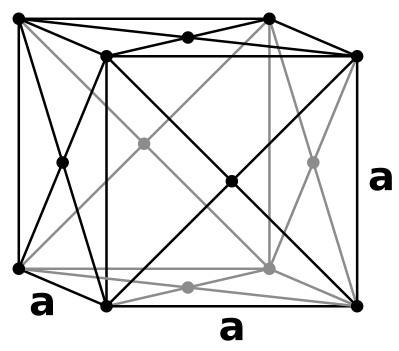
[註1] Johannes Kepler於1611年提出如果要在三維空間中堆積大小相同的球體，最節省空間方法是市場小販堆疊橘子或番茄的方式，如文章一開始的圖一。這樣的方法又稱為面心堆積，等效上如下圖之立方體。

　　左圖所示為一個立方體，在化學稱為「晶格」（lattice）。每個點都是一個球的球心，立方體的6個面還有8個頂點皆各自有一個。每個面上的點所代表的球有一半的體積落在立方體內，頂點所代表的球則有1/8落在立方體內。因此等效上立方體內共有¹?₈?×?8+¹?₂?×?6 = 4個球。進一步的數學計算可以說明球的體積（4顆球）約佔了整體空間（一個晶格）的74％。

[註2] 其代表人就是著名的畢達哥拉斯（Pythagoras），傳說中他發現畢氏定理，然而在數學史、哲學史上並沒有足夠的資料可以證明。因此本文以畢達哥拉斯學派稱呼。

[註3] 參加演講的聽眾有一些高中生，相信這些朋友們在「數與坐標系」的單元中有學到，√2就無法化為簡單整數比。項教授在演講中，則舉了另一個例子。

[註4] 參見MathWorld中關於Kepler Conjecture的條目。負面評述的例子請見《刻卜勒的猜想》，天下文化出版

[註5] 在1998年Thomas Hales以窮舉法（Proof by exhaustion）配合現代電腦處理了5000種可能的情形。但台大數學系張海潮教授面對項教授的批評者，曾反駁Hales的方法太過複雜，在交給電腦的同時，已經阻絕了一般數學家對這問題的了解。（《科學人雜誌》書評〈數學接力賽〉，2005年11月號）

?

責任編輯：MissZoe
分享到facebook