都市化的普世特徵？！

■我們常在物理問題中追求一些普世性的特徵。無獨有偶，在都市發展的研究中，學者也發現一些普世性的都市化脈絡。

撰文｜蕭維翰

理論物理學除了研究領域有許多分支外，在追求的問題上也有各式不同的品味。有些學者喜歡針對特定問題計算獲得明確的數字和實驗比較，也有些人傾向研究不同問題間的關聯性，希望可以挖掘出一些普世性的特徵（universality）。

後者最負盛名的典範大抵是重整化群（renormalization group）在臨界現象（也就是像水與水蒸汽之間、鐵磁性與順磁性間的相變化）的研究，屏除太過於技術性的說明，（1970年後的）重整化群提供一個思考的典範，用以理解在實驗上表現的一些物理事實──比如細節上很不一樣的系統，像是由不同分子組成的氣體，在臨界點時，某些實驗曲線在調整尺度後都有一樣的特徵，也就是這種性質跟它是二氧化碳、水，抑或其他氣體無關。

這種思路與技巧不只能被應用在物理問題上，在重整化技術有突破貢獻的 Leo Kadanoff 就曾有幾年花時間在思考都市發展的問題。本文便想介紹最近出爐的一篇文章，著力於探討都市化是不是也有一些普世性的特徵。[參1]

遠在重整化群成熟以前，臨界現象便已有許多相關實驗，理論學家再透過實驗提供的線索，去發想適當的描述方式。類似地，現在這些都市演化的研究也得利於一些地理資料的公開化，而在參考資料[1] 中，作者們便透過可取得的資料庫進行了芝加哥、倫敦、紐約及巴黎四個都市人口與建物幾百年來的演化情形。在現象學的層次，發現在都市發展的過程中，這四個都市的確都不約而同地經歷了三個「相」（從文內可以發現，芝加哥市因為發展起步較晚，第三個相並不明顯）：

1. 建築和人口同時快速成長。
2. 由於住宅區轉變為辦公地區和商店區，建物數量持平，但居民人口減少。
3. 人口和建築數量再次成長。

有了數據，下一步便是說明都市化的模型。在這篇文章中，作者們提供了一個簡易的模型來描述前兩個相間的變化。若我們用 N 與 P 來代表建築物數量與人口數量，則在前兩個相的變化間需要有一個轉捩點 N* 與 P*，在這個點之後，建物數量約略持平，但人口減少。給定一個都市的區域，我們可以設想將這塊面積劃分成許多小方格，每個方格上可以是有建築物或者沒有建築物。若方格上是有建築物的，則又可將建築物的樓層區分為商用樓層或居住用樓層，並且假設平均而言，每個居住樓層可以容納ΔP 個住戶。

整個都市的演化則如下所述，從時間 t 演化到 t +Δt ，我們隨機選擇一個方格，如果這地方是沒有建築物的，則讓他蓋一層居住用樓層，並且總人口數增加ΔP，建物數增加 1。假如抽樣的方格已經有建築，則建物數量不變，但我們可以考慮樓層的重新分配，在此模型中，他們想像有 p_h 的機率在原有的建物上多蓋一層居住用樓層，隨之總人口數也增加ΔP，另一方面也有 p_c 的機率將現有的一層居住用樓層轉變為商用樓層，相對應的總人口數減少 ΔP，剩下 1-p_h-p_c的機率什麼事都不發生。

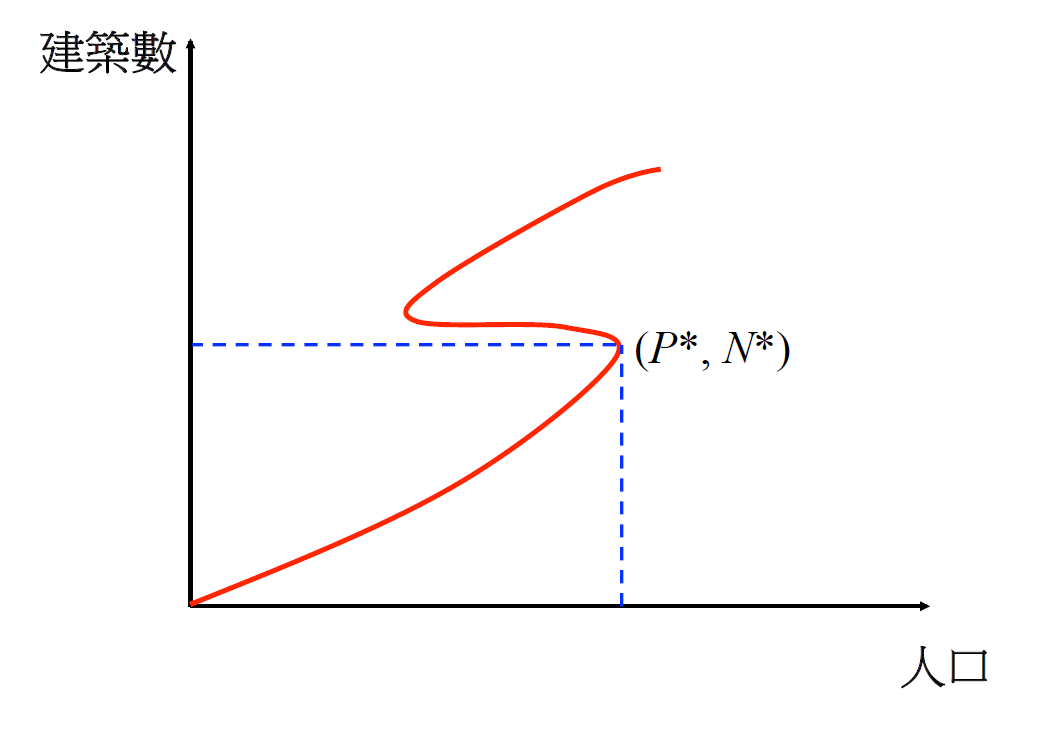
上面這幾個步驟，約略模擬了建物增加、住戶擴建與商住互易的現象，定量上整個問題則被三個參數ΔP、p_h與p_c 決定。不難想見，轉捩點只在p_c>p_h的時候可以發生，重新定義變量後（約略而言是將變量去單位化，這樣結果就不會跟細節的時空間尺度有關係。）他們發現這個模型預測的結果和數據十分切合——不同的都市、不同的年代的都市化進程，在調整尺度後落在同一個曲線上。

雖然有趣，但我們其實還有很多問題可以深究，比如第二相與第三相之間的有效描述是什麼，哪一種機制使得市區人口回升？或者針對前述的有效理論，能不能有其他的模型預測出類似的曲線？

還有一個觀點是，當我們認真探討一件問題的普世特徵時，那麼到頭來我們對於這個問題其實沒學到什麼[參2]， 因為普世性表示這是大家共享的特質，然而相較於解析各大都市如何以一致的趨勢發展，窺探它們別緻僅有的風華，或許更引人入勝。

參考資料：
[1] Giulia Carra and Marc Barthelemy, The Fundamental Diagram of Urbanization, arXiv: 1609.06982 (2016).
[2] Nigel Goldenfeld, Critical Phenomena (A talk given at Kadanoff Memorial Symposium)

--
作者：蕭維翰，臺大物理系畢業後逃到芝加哥，吹風吹雪之餘，做研究讀博士班。可惜離開臺灣後無海可看，只能在密西根湖旁揀一方堤岸，偽裝成看海的人。科教中心特約寫手，從事科普文章寫作。