千變萬化的流體(三):哥吉拉雲—流體的不穩定性
海岸邊的雲層上緣,出現一隻隻如同哥吉拉形狀的雲;原子彈投下後,劇烈爆炸引起的蕈狀雲;土星大氣層內形狀獨特的雲帶…等。這些看似毫無相關的現象,背後其實成因都可以歸納為:流體中的不穩定性。
撰文/劉詠鯤
2020年在青森縣的海邊,有網友分享了一張雲朵彷彿在進行「哥吉拉大遊行」的照片(圖一左上);也有飛行員在雲層上分享過類似的照片(圖一右上);除此之外,天文學家在土星的大氣層也觀察到相似形狀的雲層(圖一下)。這些「哥吉拉」的行動力竟然如此之高,不只在地球上出現,連土星上都有。這是否暗示它們背後其實具有相同的形成機制呢?

在<千變萬化的流體(一)>一文中,我們介紹了流體流動的狀態主要可以分成兩種:層流與紊流。層流狀態的流體十分穩定,它可以被視為一層一層獨立的流動來討論;相對的,紊流如同它的名字所表示,流體內部的流動較為混亂,不同層之間的流體會互相混合、影響。而決定是層流還是紊流的關鍵因素便是「不穩定性」[1]。
在描述天氣系統為甚麼難以預測時,常常會提到「蝴蝶效應」這個小故事:位在大西洋的颶風,其成因可能只是在亞馬遜森林裡面一隻蝴蝶煽動了翅膀,這個初始的小擾動,隨著時間演變,最終形成尺度龐大的結構。不穩定性在流體中扮演的角色也十分相似。起初流體內部隨機的產生十分微小的擾動,若整個流體的不穩定性足夠大,微小的擾動便有機會繼續成長,直到對整個流體都造成影響。流體中具有各式各樣的不穩定性,在本篇文章中,我們將會介紹與哥吉拉雲還有蕈狀雲有關的兩種不穩定性:克耳文-亥姆霍茲不穩定性以及瑞利-泰勒不穩定性。
●克耳文-亥姆霍茲不穩定性
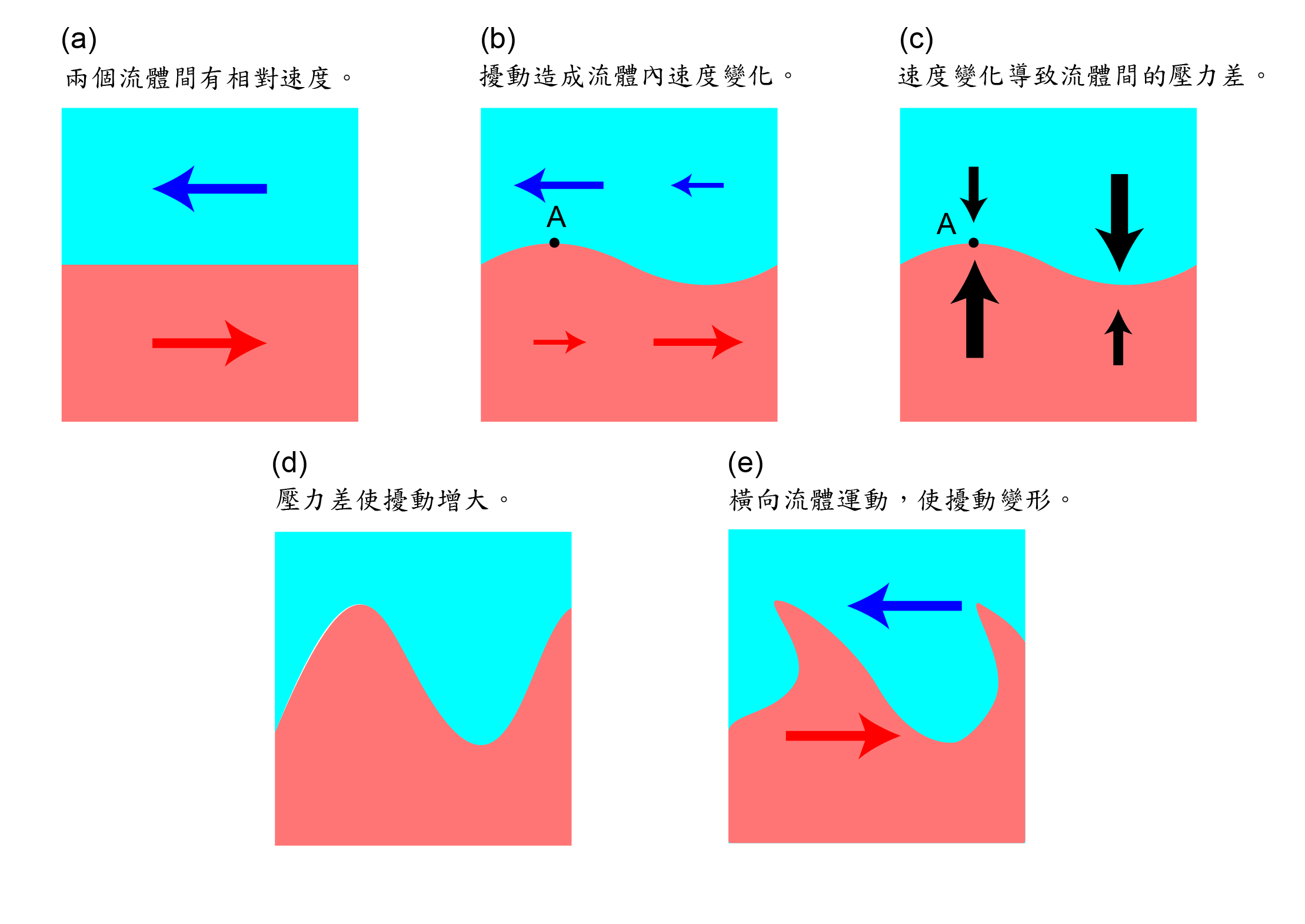
這個不穩定性得名於兩位對此現象進行研究的物理學家:發明絕對溫標的克耳文爵士,以及對聲學共振系統做出系統性研究的亥姆霍茲(在<香檳聲音哪裡來?>一文中,他曾經登場過)。這個不穩定性發生的條件是:兩層流體之間具有相對速度。
請搭配圖二,讓我們一起來理解這個不穩定性是如何產生哥吉拉雲的。假設有兩層流體,分別向左與向右運動。當它們彼此完美平行時,一切無事,如圖二(a)。但這個狀態其實並不穩定,任何的擾動,都可能會破壞這個完美狀態。例如,流體中形成了如圖二(b)的擾動,接下來流體的運動會如何變化呢?
對於淺藍流體來說,A點的體積較原本略小,因此流動速度較大,如同澆花時,將水管捏住(管徑縮小),水可以噴得更遠。此外,流速較快也會使得A點的壓力減小;但對於紅色流體來說,A點的壓力反而會增大。如此會導致流體內部的壓力分佈形成圖二(c)。兩種流體之間的壓力差,會進一步使擾動長大,如圖二(d)。最後,由於流體本身橫向的速度,使擾動在橫向上出現變形,如圖二(e)。如此一來,哥吉拉形狀是不是就出現了呢?
●瑞利-泰勒不穩定性
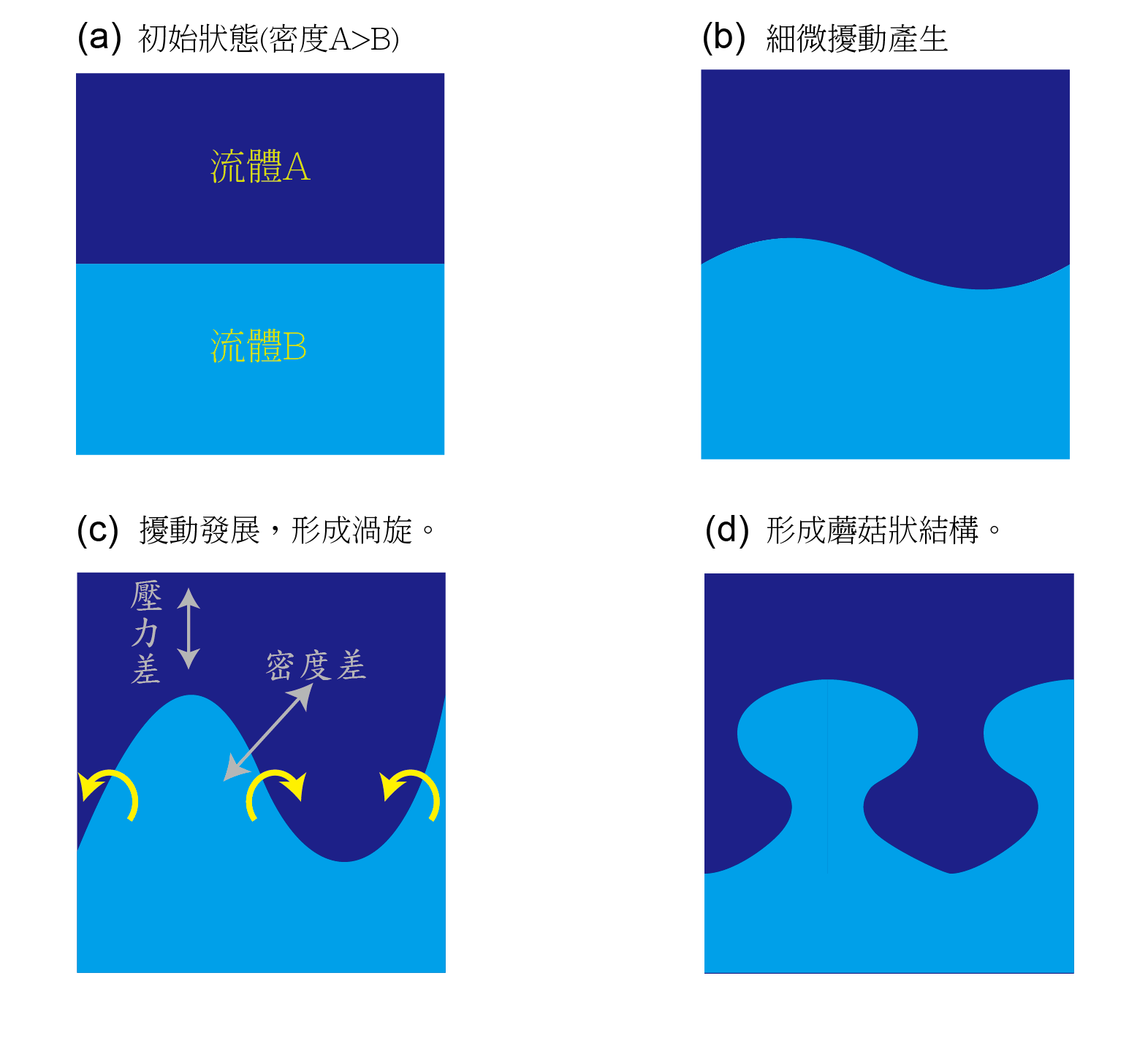
接下來,讓我們來看另一種在生活中沒那麼常見,但是看過就很難忘記的不穩定性現象:核爆產生的蘑菇雲。這種現象的成因,是來自於瑞利-泰勒不穩定性,它會發生於密度較大的流體壓在密度小的流體之上時。核彈爆發會在極短時間內釋放出極大熱量,將爆炸中心的空氣瞬間加溫。我們知道,氣體的溫度越高,密度越低,因此在爆炸中心,會瞬間形成大量的低密度空氣。
讓我們用簡單的模型來看看,這種不穩定性是如何造成蘑菇雲的。圖三(a)中有兩種流體,密度較高的在上,此時整個流體系統處於不穩定態,只要有一點擾動(圖三b),不穩定性就會使擾動擴大。由於密度差異,重力使得密度小的流體上升,密度大的下降,使不穩定度振幅逐漸增大。此外,由於壓力差與密度差的方向並不平行,會導致流體的邊界形成渦旋(圖三c)。以上這些效應疊加在一起後[2],流體邊界處便會逐漸形成如蘑菇狀的特徵(圖三d)。
以上兩種流體不穩定性,其實在我們生活中也存在,例如:點燃的線香。由於線香燃燒處的溫度上升,空氣密度下降,此時就滿足瑞利-泰勒不穩定性的條件;當熱空氣上升時,和兩側靜止的空氣有一相對速度,也滿足了克爾文-亥姆霍茲不穩定性條件。只是由於規模較小,發生速度較快,肉眼未必可以清楚的看到如前文中提到的明顯特徵。儘管如此,各位讀者在了解這些不穩定性之後,若是試著觀察看看生活中的各種流體,也許也能找到隱藏起來的「蕈狀雲」喔!
--
註解:
[1] 更詳盡的說明可以參考CASE<上下顛倒漂浮船>一文
[2] 實際上,形成蘑菇狀構造還與流體在三維條件下的非線性效應有關,數學模型較為複雜,此處只是簡單概述其成因。
--
參考資料:
- Kelvin–Helmholtz instability
- Rayleigh–Taylor instability
- “Single mode hydrodynamic instabilities” draft from Hideaki Takabe.
