何處停車？物理學家的停車策略

當騎著U-bike到停車站時，面對眼前的這個空位，究竟是要放棄它繼續往下騎，期待著離捷運出口更近的空位，但卻會冒著其他位置都滿，結果只能被迫折返的風險呢，還是保守的選擇它，但看見後面滿滿的空位，最後懊悔自己多走了一大段路。究竟怎樣的選擇是最有效率的? 波斯頓大學的兩位統計物理學家Krapivsky和Redner 在Journal of Statistical Mechanics上發表了他們的研究。

編譯／鮑彥滕

在Krapivsky和Redner的模型中，他們以時間花費作為衡量效率的量尺。當然，離目的地最近的車位可以走最少的路，但可能要多耗費折返的時間來發現它。於是駕駛員面對空位的取捨影響了他們停完車再走到目的地需要耗費的時間。Redner 說:「數學讓你能做最聰明的選擇，它讓你能洞悉這個複雜的世界」。

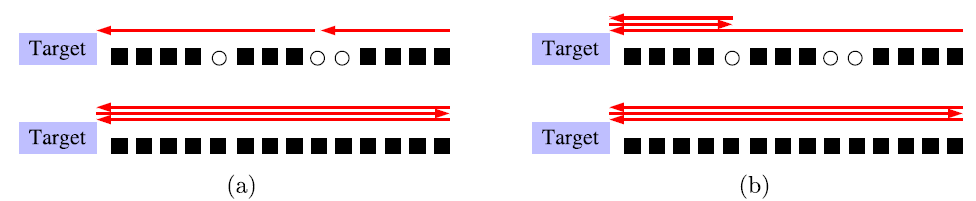
Krapivsky和Redner在論文中針對一個理想一維的停車場(圖一)提出了三種選擇策略，分別是溫順(meek)、謹慎(prudence)和樂觀(optimistic)，溫順的駕駛員在進入停車場時會停在最右邊，而謹慎的駕駛員會停在第一個空隙的最左，至於樂觀的駕駛則是會開到底，折返停在離目標最近的空位，後面兩種策略若是遇到車陣中沒有空位的情況則折返停在最右邊(圖二)。

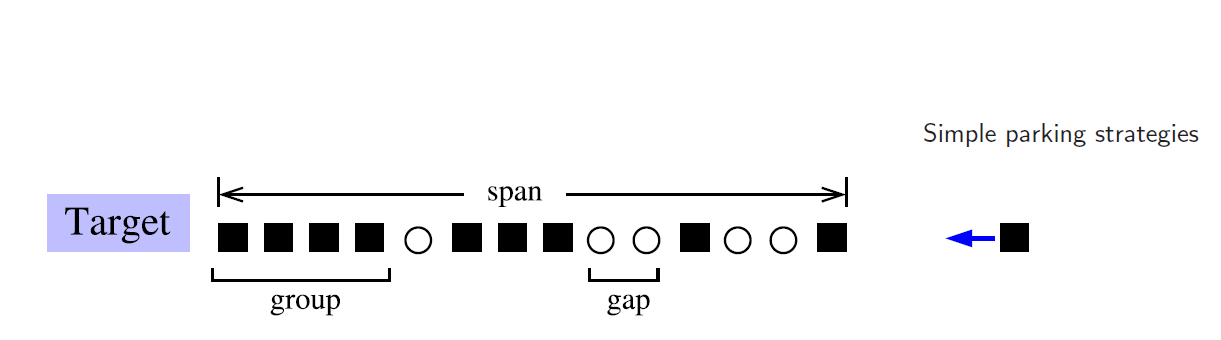
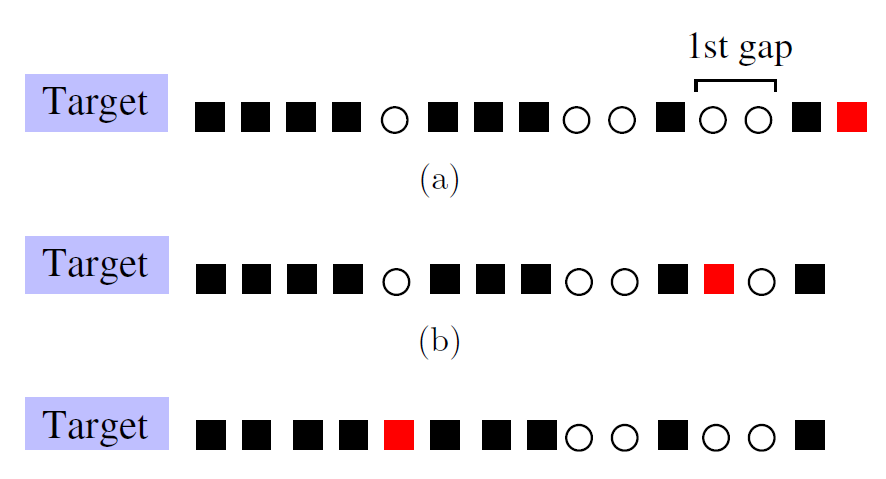
溫順的駕駛員

很有趣的是，車子一台接著一台接在最後面的行為可以類比為人體中微管搭建的機制，在Krapivsky和Redner的論文之中便直接利用了描述微管動力學的方程來解決這個數學難題。他們的結論是這個策略的效率非常差:整個停車的間距會被拉得非常長(正比於e^λ，λ為車的流率)，然而車卻都集中在入口處(圖三)。在某些情況下使得停車場全空，此時整個停車的長度會重新增長。再一次的，這樣全空的事件與當微管的活化端只有GDP單體時造成的崩潰十分相似。

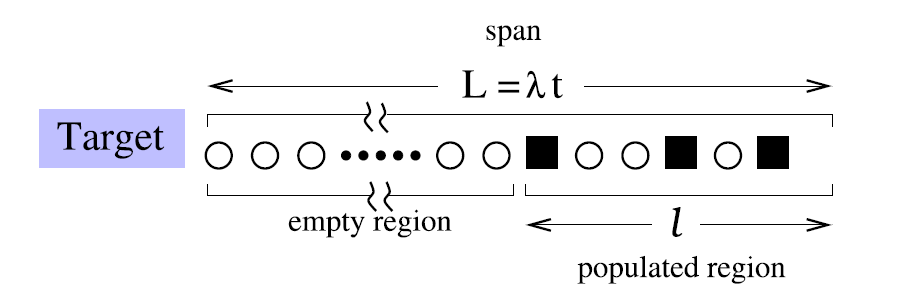
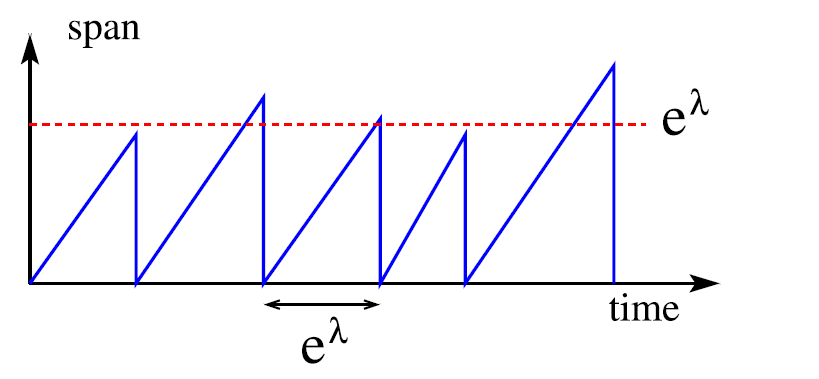
樂觀和謹慎的駕駛員

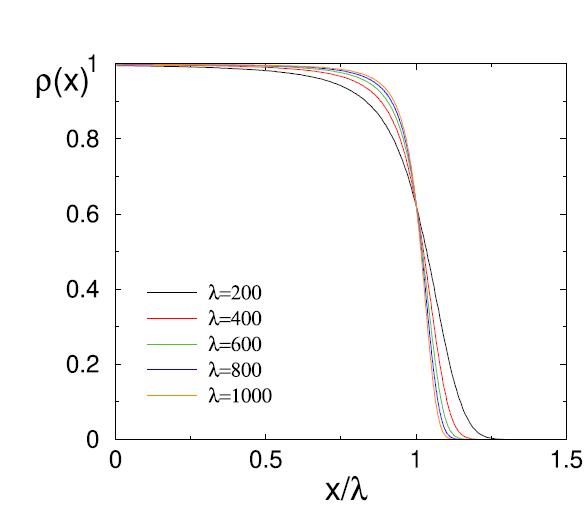
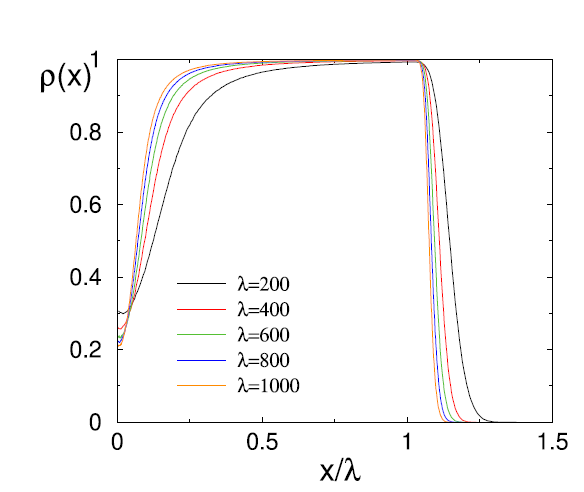
在樂觀策略的分析上，Krapivsky和Redner在微分方程的求解上把不同位置有車停的期望值近似為個別期望值的相乘來簡化這個問題，在與電腦模擬比對後得到非常接近的結果。在樂觀策略上，車輛幾乎全集中在最左邊(圖五)。而這些有車的區域是空格的機率會與車的流率和它所在的位置相關。

至於樂觀策略，由於計算上的困難，Krapivsky和Redner利用模擬得到了(圖六)的結果，其顯示在目標附近仍有許多的空位，原因是來自駕駛只會將車停在第一個空格的最左，而更深入的位置便不會停。可以發現上述兩者策略在位置大於λ的地方會有很大的落差，原因是因為當時間夠長達到平衡時，停車場中的車數會等於車的流率。

最有效率的策略

對於溫順策略，新進的駕駛會將車停在間距的最右端，其長度正比於e^λ，其指數增長相對於其他兩者顯得沒效率，不過當部分的駕駛使用其他兩種策略時，駕駛可以很幸運地停在距離λ的位置。

而對於樂觀和謹慎兩者策略，雖然樂觀的駕駛員總是比謹慎的駕駛員有更大的機率找到最接近的車位，但這個策略必定需要折返，平均下來花費的時間比使用謹慎策略的駕駛員要長。(圖七)

Krapivsky和Redner最後得到了溫順、謹慎和樂觀三種策略之中，謹慎的策略具有相對高的效率，但是他們也提到在現實生活中駕駛更多的是依靠直覺，所謂「最理想」的策略對研究者依舊是個迷人的挑戰。

編譯來源:ScienceDaily 2019/09/19 Where to park your car, according to math

參考資料:
[1]P. L. Krapivsky, S. Redner, and E. Ben-Naim, A kinetic view of statistical physics. Cambridge University Press, 2010.
[2]P. L. Krapivsky and S. Redner, "Simple Parking Strategies," vol. 2019, no. 9, 2019.