Hubbard 模型(四):費米 Hubbard 模型:簡單的解析事實(下)
■緊接著上文,我們在此介紹費米 Hubbard 模型中怎麼產生鐵磁性。
 撰文|蕭維翰
撰文|蕭維翰
在前文中我們定義了費米 Hubbard 模型,並花了一點空間討論當躍遷常數 t 與交互作用 U 都不為零,但後者遠大於前者的時候,透過一個二階的量子過程,半填滿的晶格在能量上會偏好相鄰的兩個費米子擁有反向的自旋,這構成了「反鐵磁性」(antiferromagnetism)的可能性。
事實上,這個物理直覺約略是正確了,但僅僅兩個節點,一般而言不太能給我們精確的「物質相」預測,因為後者往往是定義在熱力學極限(thermodynamic limit),意指在系統自由度趨近無限大的時候。
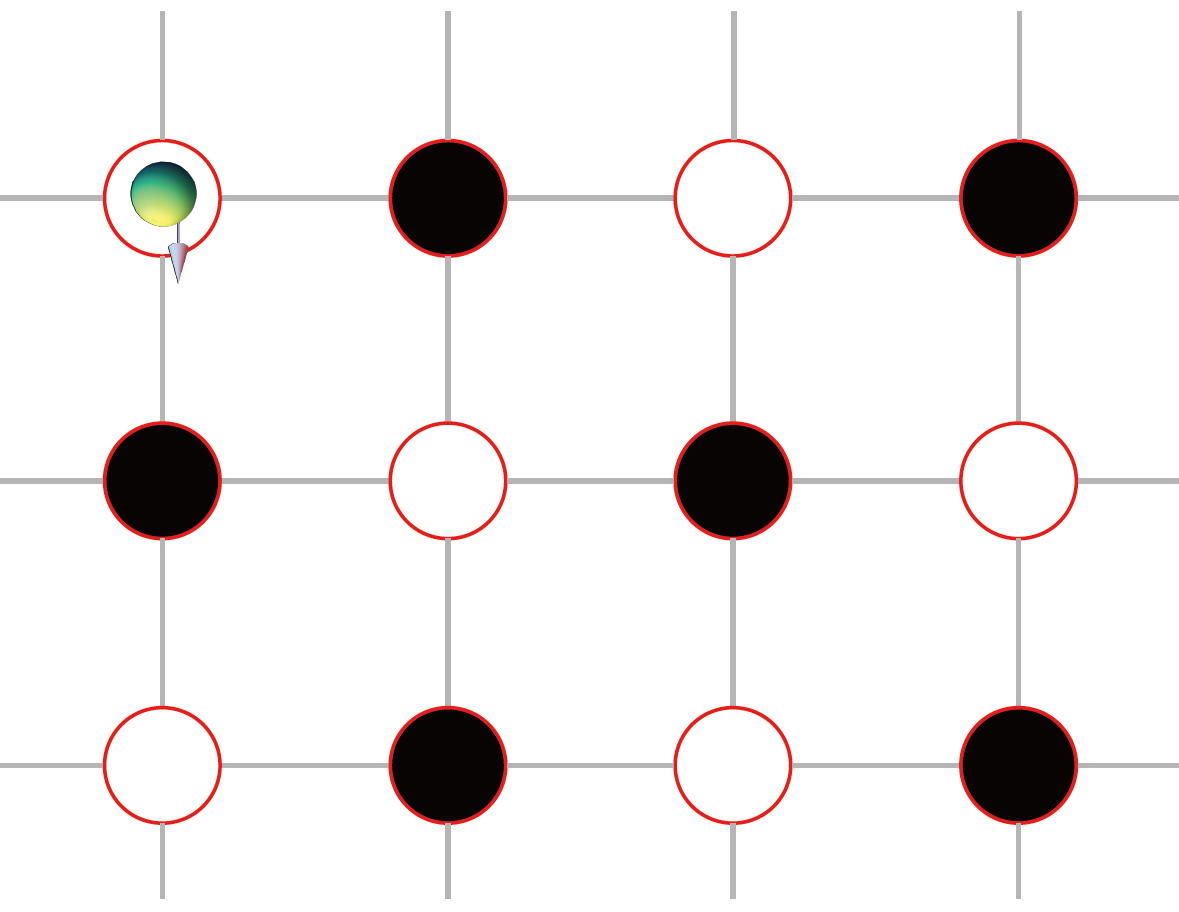
在最簡單的立方晶格,並考慮費米子僅僅能在相鄰的節點間躍遷,讀者可以說服自己,這樣的晶格其實可以像圖二所示一樣,區分為兩個子晶格,分別由白色圓圈和黑色圓圈表示。根據我們的假設,粒子的躍遷只能讓它們從黑跳到白或白跳到黑,而不能直接在同色圓圈之間躍遷。當一個晶格可以被區分為這樣兩部分時,數學上可以證明基態的總自旋量是兩類圓圈數目的差除以 2(Lieb 定理)。在圖一這樣簡單的幾何中,黑色圓圈和白色圓圈的數目是一樣的,因而基態的自旋角動量為 0 ,因而在可數的系統中,我們至少可以確定基態的總自旋角動量是 0。
嚴格來說,上述這個在有限系統證明的數學定理沒有辦法直接推廣到決定物質相所需要的熱力學極限,我們能說的只是在這個狀況下不具有鐵磁性,而反鐵磁相這個推測則需要更精確的計算去證實。
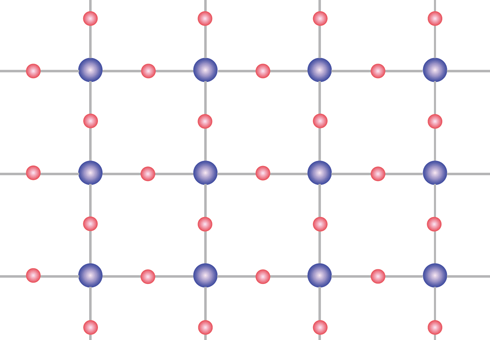
有趣的是,當我們換個幾何結構,見圖一,這樣的晶格結構可以在 CuO 之類的化合物被發現,它符合前面分為兩個子晶格的規則(在本圖中為藍色圓圈及紅色圓圈)但這兩種圓圈的數目顯然是不一樣的。如果晶格的尺寸為L*L,那麼我們有L*L個藍色,但卻有2L*L個紅色,根據上面的數學定理,總共的角動量為L2/2。注意這並不是鐵磁性,因為若是在鐵磁相,所有的自旋都指向同一個方向,則我們應該要有3L2 。這裡的淨磁矩,或說自旋,並不是因為相鄰的費米子們喜歡將自旋擺在同一個方向,只是因為其中一個方向的數目比另一個方向多得多,因而累積出的巨觀磁矩,這種有一點淨磁矩但還差鐵磁一段路的性質,通常稱為亞鐵磁性(ferrimagnetism)。
上面這個例子也告訴我們,儘管我們透過一些小小的量子力學模型(比如說前文中兩個節點、兩個粒子的玩具模型)來幫助我們建立直覺,真的巨觀系統的結果往往還能有許多變化,而我們之前一直忽略的晶格的幾何,也常常對物質相產生影響,類似的故事在之後討論臨界現象時將再次出現。
經歷幾篇文章的疲勞轟炸,我們已經掌握一些關於費米 Hubbard 模型的小直覺(1)在 U =0 極限系統沒有鐵磁性(2)半填滿與強交互作用下,相鄰的晶格比較偏好反鐵磁性。若我們想要探究鐵磁性有沒有可能在這個模型中發生,第一件事情告訴我們,鐵磁性必然跟交互作用有關。事實上數學上也可以證明,假設我們在 U = 0 的極限有明確定義的單粒子能譜,那麼打開交互作用後,交互作用的大小至少要大於整個費米海的深度,才有可能有鐵磁性。第二件事情告訴我們,即便有了交互作用,想要獲得鐵磁性,我們還得遠離半填滿的狀態,也就是我們要考慮一個系統,平均每個節點上沒有一個粒子。
從之前培養的直覺得到一些啟示後,又一次我們來看看有沒有簡單的模型,能夠幫助我們培養新的直覺並洞悉任何可以產生鐵磁性的機制。
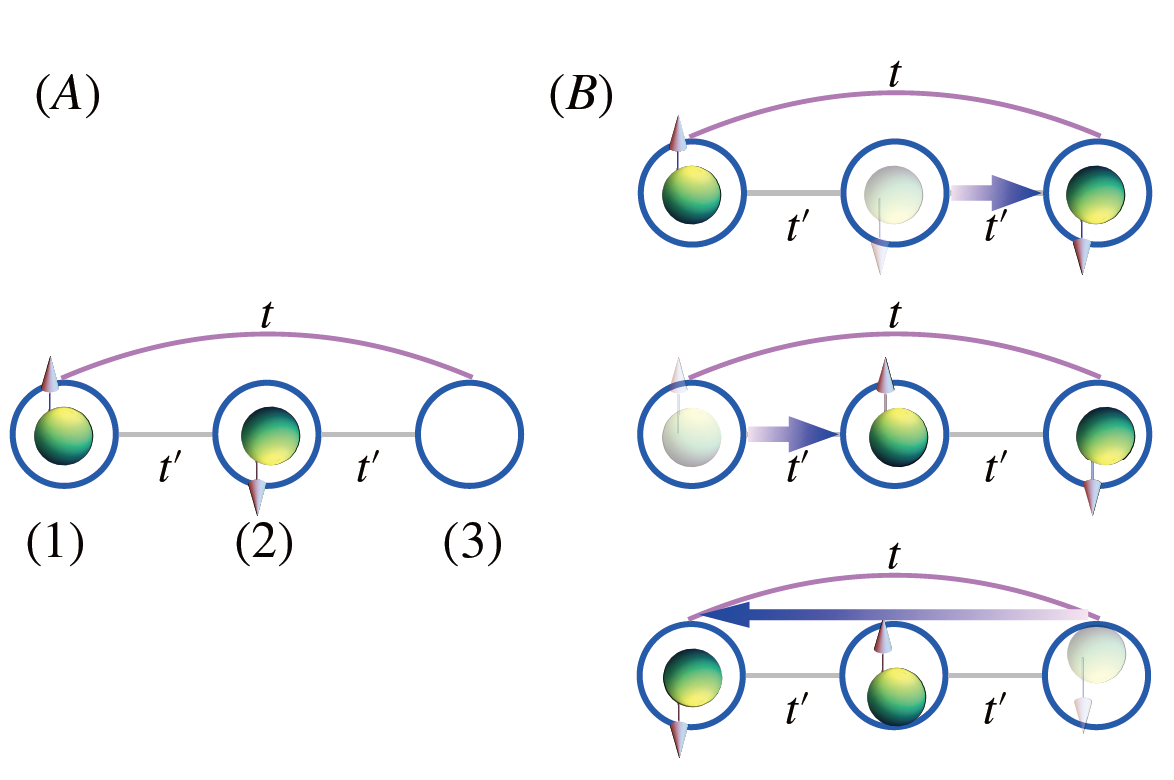
讓我們看看圖 三(A) ,在這邊我們考慮三個節點,並且在裡面放兩個費米子,一個自旋向上,一個自旋向下。跟之前的分析都不一樣的是,我們考慮允許不同節點間有不同的躍遷常數:在節點 (1) 與 (2) 和節點 (2) 與 (3) 之間,躍遷常數是t’,而在節點 (1) 與 (3) 之間,躍遷常數是 t 。
乍看之下,這個系統有一個自旋向上,一個自旋向下的粒子,加起來的自旋應該是 0—這並不是故事的全貌,因為我們畫的箭頭通常是指自旋在 z 方向的投影,因此我們只能說這個組態在 z 方向沒有淨自旋,我們並沒有辦法光看著圖 2(A) 就決定系統基態的總自旋。在兩個自旋 1/2 粒子組成的系統,總自旋可以是自旋 0 或者自旋 1,前者的 Sz 毫無選擇只能是 0 ,然而自旋 1 可以有 Sz=±1,0 ,也因此我們要來看這個模型的基態,是自旋 0 ,還是自旋 1。
稍稍插播一點量子力學知識,如圖三(A) 一樣的組合,需要與兩個自旋交換後的狀態進行組合,才能變成自旋 0 或者自旋 1。在完整的計算之前,這提供了我們一點線索,集中精神到關鍵的物理上—我們來看看有哪些機制可以讓圖 2(A) 中的兩個自旋對調。為了方便初步的圖解,我們再一次考慮 U 很大的極限(所以忽略掉兩個粒子塞到同一個點上的可能性)我們把(一種)完整的步驟畫在圖 2(B),首先我們讓 (2) 的粒子移到 (3),然後把 (1) 的粒子移到 (2),再把 (3) 的粒子移到 (1)。這樣三步驟的過程給我們的振幅給我們兩個 t’ 跟一個 t 。經驗告訴我們 t’ 與 t 是否同號將會影響計算的結果。
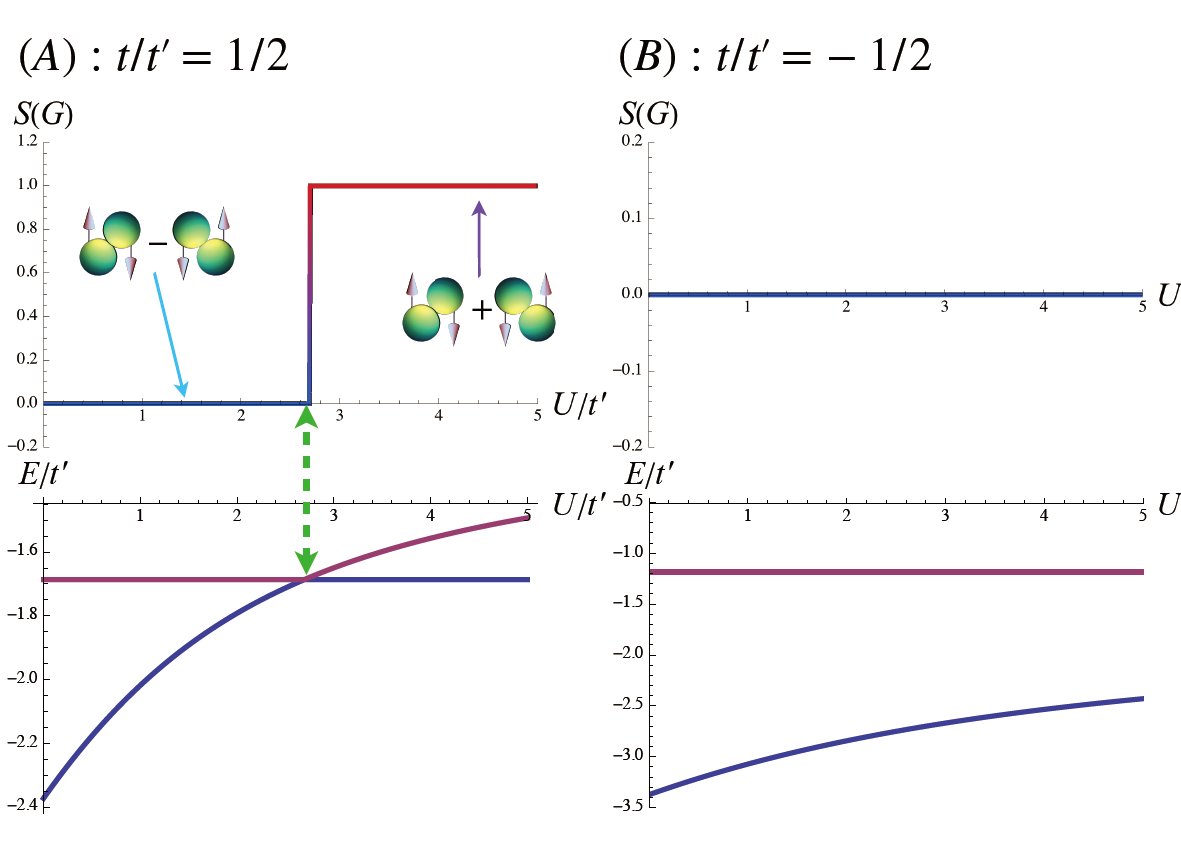
然後我們進行認真的計算,考慮任意的 U 值,這問題基本上不難,是個連筆者都會的 9*9 矩陣。我們在圖四A、B 中分別考慮 t’,t 同號與異號的情況,畫出了最低能量態的自旋量子數與最低的兩個能量隨著 U 值的變化。我們發現 圖四B 中,基態的自旋基本為 0 ,並且在能量的順位上並沒有什麼變動。圖四A 則比較有趣,我們發現當 U 值大於一定程度的時候,最低能量的組態出現了交叉,並且基態的自旋從 0 跳到了 1!也就是存在著產生鐵磁性的機制。
這同時也部份驗證了我們的直覺:t’,t 異同號與足夠大的交互作用,對於系統的磁性都有關鍵的影響。
針對於一些簡單物理圖像的討論,筆者就暫時打住。下一篇文章開始,讓我們嘗試研究半填滿 Hubbard 模型的量子相變化。
參考資料:H. Tasaki, arXiv: cond-mat/9512169 (1997).
本系列全文:
Hubbard 模型(三):費米 Hubbard 模型:簡單的解析事實(上)
Hubbard 模型(四):費米 Hubbard 模型:簡單的解析事實(下)
--
作者:蕭維翰,臺大物理系畢業後逃到芝加哥,吹風吹雪之餘,做研究讀博士班。可惜離開臺灣後無海可看,只能在密西根湖旁揀一方堤岸,偽裝成看海的人。科教中心特約寫手,從事科普文章寫作。
