Hubbard 模型(三):費米 Hubbard 模型:簡單的解析事實(上)
■我們首先介紹在費米 Hubbard 模型中一些可由直覺跟解析解理解的事實。
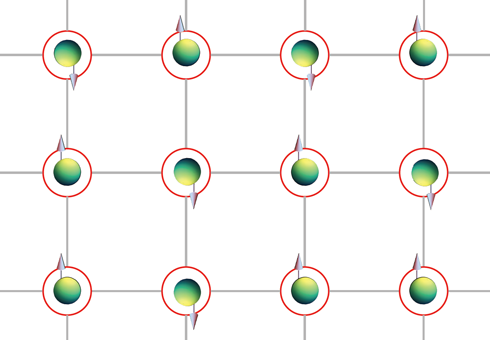
由於不相容原理,當系統沒有躍遷能力的時候,費米 Hubbard 模型最低能量的組合便是盡可能地讓每個粒子都佔有一個晶格點。
撰文|蕭維翰
經歷了前面兩篇暖身,有忍住讀完的讀者們應該稍微對 Hubbard 模型有了基本的了解。本文中我們繼續考慮類似的模型,但在這裡我們把粒子們換成費米子。
費米子與玻色子的根本差異在於前者遵守庖立不相容原理(Pauli Exclusion Principle),一個系統內不會有兩個具有一模一樣量子數的費米子,這也將大大的影響我們對基態物質相的分析。舉個實際例子,如果我們考慮不帶自旋的費米子,則兩個粒子出現在同一個節點上不僅僅是會增加能量這麼簡單,而是根本不允許發生。在接下來的討論中,為了更切合電子的特性,我們將考慮自旋 1/2 的費米子,儘管結構簡單,但(1)這種 Hubbard 模型的基態被認為跟高溫超導體具有一樣的相圖(phase diagram); (2)數學上幾乎是不可能完全的解開的。
基於它的困難與蘊藏的豐富物理,它幾乎是固態物理中最重要的模型之一。
由於題材的浩大與他在近代固態物理中的重要性,筆者又將費米 Hubbard 模型細分,在本文中首先討論一些簡單但精確的數學結果,之後我們還將從臨界現象(critical phenomenon)、量子相變化(quantum phase transition)的角度切入,之後獨立地回顧一下近年在實驗上的進展。
我們分析的邏輯跟前文還是很接近的:這個模型基本上是兩種能量尺度在對抗,一個是粒子在晶格上跳躍的能力 t,另一個是粒子間交互作用的強度 U。我們首先分別分析其中一個效應佔優勢的極限,並嘗試去推測當兩者旗鼓相當時,系統的基態該是什麼樣子。
(1) U=0 。
在這個極限中,費米子們基本上看不見對方。(這個陳述其實不是很精確,因為事實上,任意一個費米子總是看得到它的同類們,不然它們無法遵守不相容原理。)多體問題在數學上等效變成了很多個單體問題,也因此我們可以計算出能階,接下來的任務就是把很多粒子放進去這個能階。和玻色子問題的相異處就在這裡顯現出來了,在這裡我們無法放任所有人都佔據最低的單粒子態,假設自旋上下的化學勢被調整得一樣,使得我們各有 N 個自旋朝上跟朝下的費米子,則基態中會費米子們會一路填滿最低的 N 個能階,形成一個費米海(Fermi sea)。
(2)t=0。
在這個極限中,費米子基本上沒有移動的能力,基態問題變成要妥善的分配費米子們的位置,使得能量可以儘量地低。因為相斥的交互作用U,使得自旋上的費米子不喜歡與自旋下的費米子處在同一個節點,而因為不相容原理,相同自旋的費米子甚至不能出現在同一個節點。假設我們考慮總粒子數少於總節點數的特殊狀況,那麼我們可以選擇讓每個節點至多只被一個費米子佔據,這些狀態都具有基態能量E = 0 * U = 0。與之前的無自旋玻色子不同的是,在這邊我們有兩種費米子,因此基態的選擇不是唯一的,而有很多簡併態,另外,這樣子的基態是個順磁性系統。
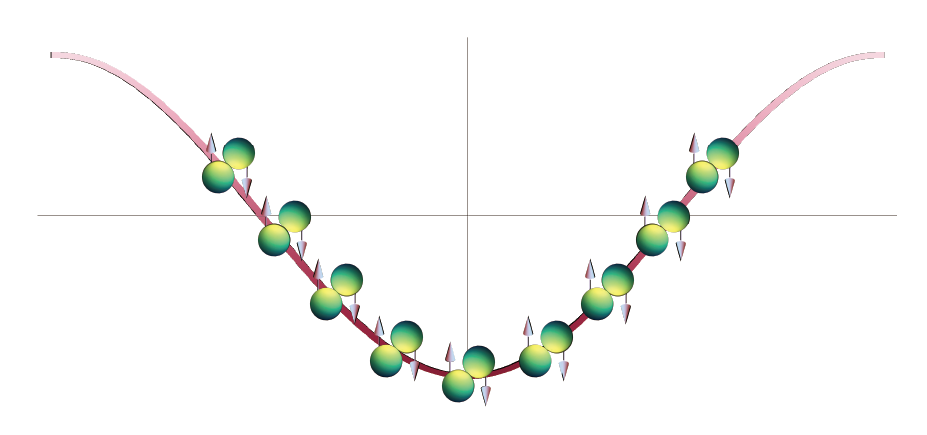
Figure2. 在沒有交互作用的狀況下,費米 Hubbard 模型的能量形成一個能帶,由於不相容原理,他們沒辦法全部聚集在最低態,而是會一路形成一個費米海。(photo credit: 作者自繪)
從上面的分析,我們瞭解到:如果粒子的數目跟節點的個數一樣多(通常我們稱這種狀態叫做半填滿(Half-filled))時,只擁有躍遷的系統,跟只有交互作用位能的系統,他們的基態都沒有什麼有趣的磁性(或說他們頂多是順磁性。)接下來我們將推論,當兩者同時存在的時候,系統的基態可以具有反鐵磁性。
要理解這個問題如何產生反鐵磁性,我們考慮U/t≫1,但是 t≠0 的情況。在有限的躍遷常數底下,一開始給定的基態有機會穿隧到不一樣的狀態。代數上,我們要計算的是,當原本的物理狀態被動能項作用之後,和原先的狀態重合度還有多大。
這其實可以用一個只有兩個節點的模型來看。由於我們考慮半填滿,那在兩個節點上,被允許的組態就只有(1)兩個自旋同向的粒子,(2)兩個自旋反向的粒子。接著讓我們分別討論它們。
(1):在 t=0 的狀況中,系統的基態是兩個粒子分別被放在不同的節點上。很快讀者可以理解到,當你把打開小小的 t, 事情根本沒有任何改變,因為庖立不相容原理,這個狀態中的費米子本來就沒有能力跳到另外一個節點上。
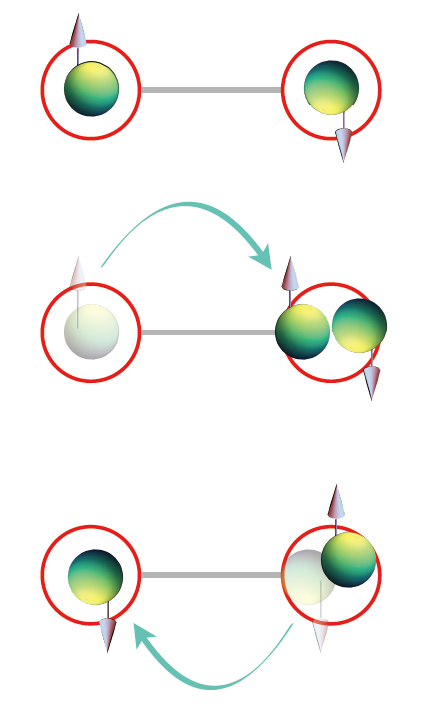
(2):在 t=0 的狀況,系統的基態依舊是兩者被分配在不同的節點上,動能項的作用可以將兩個粒子透過一次躍遷放到同一個節點上,這被庖立不相容原理允許,但要付出能量 U 的代價。但這個狀態跟原本的基態是沒有重疊的,因此只作用一次動能項對於基態的能量並沒有影響。有趣的物理發生在第二次躍遷的時候,這時系統可以回到原本的組態,因而跟原狀態產生有限的重合,更重要的是,這樣的過程可以稍稍降低系統的能量,大小為 t2/U。
讓我們梳理一下結論,在 t=0 的極限中,(1)跟(2)本來是有一樣能量的(都是 0),但在打開小小的 t 之後,我們發現(1)不為所動,但(2)可以藉由二階段的躍遷過程降低能量,因此在有限的 t 作用下,系統會偏好兩個粒子具有不同方向的自旋,這就是一種產生反鐵磁性的機制。
兩個節點的分析,雖然有辦法說明為什麼系統可能會偏好某些自旋組態,卻沒辦法決定一個大系統的總磁化程度。事實上根據完整晶格允許的分割方式,半填滿的費米 Hubbard 模型除了有反鐵磁相,也可能具有亞鐵磁性。
我們計畫下一篇文章中討論 Hubbard 模型可以透過什麼機制獲得亞鐵磁或者鐵磁性。
參考資料:H. Tasaki, arXiv: cond-mat/9512169 (1997).
本系列全文:
Hubbard 模型(三):費米 Hubbard 模型:簡單的解析事實(上)
Hubbard 模型(四):費米 Hubbard 模型:簡單的解析事實(下)
--
作者:蕭維翰,臺大物理系畢業後逃到芝加哥,吹風吹雪之餘,做研究讀博士班。可惜離開臺灣後無海可看,只能在密西根湖旁揀一方堤岸,偽裝成看海的人。科教中心特約寫手,從事科普文章寫作。
