Hubbard 模型（二）：玻色 Hubbard 模型

2018 年 11 月 26 日2018 年 12 月 14 日 CASE PRESS Hubbard, 玻色子, 莫特絕緣體

分享至

■簡單的玻色 Hubbard 模型，在 2 維空間中提供我們了解莫特絕緣體與超流體間的相變化。

撰文｜蕭維翰

希望筆者在前文中或多或少給了一點理由讓大家一起來賞玩原本只屬於一部分物理學家們的玩具。現在開始我們進入正題來探討 Hubbard 模型家族中的幾個知名典範。明確的說，首先我們討論在二維空間中正方晶格（square lattice）上的玻色子版本 Hubbard 模型（Bosonic Hubbard Model）[1,2]。

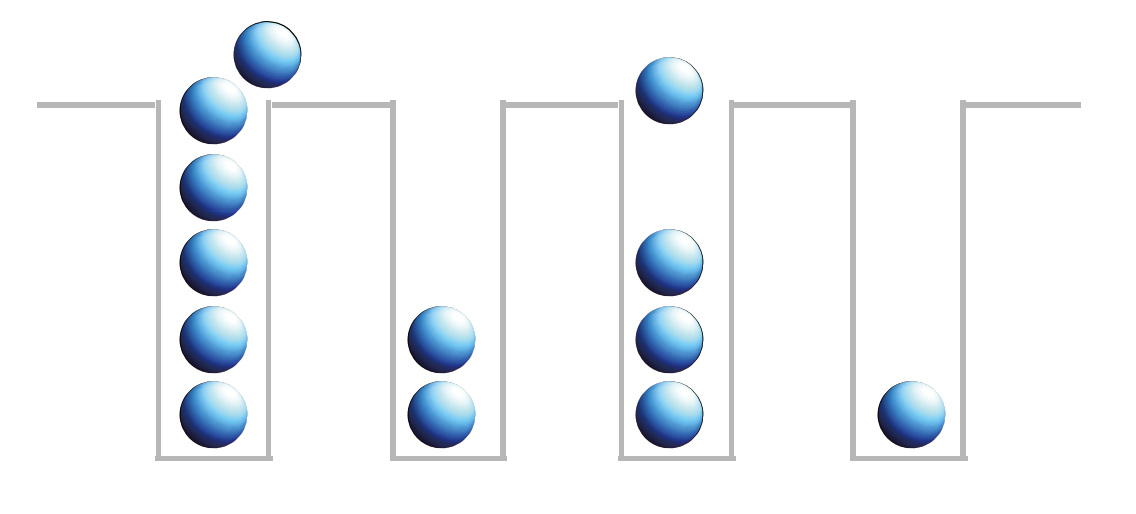
也就是說，我們有一個正方形的晶格，並有一些玻色子被放在節點 x_i上，這些玻色子可以相鄰的兩點上移動，但當兩個玻色子聚集在同一個節點時，他們看得到彼此並且兩者間會感受到排斥力。代數上，玻色子的數目、玻色子在節點上移動的能力、與同一節點上兩個玻色子的排斥力可分別由化學勢 μ（chemical potential）、躍遷常數 t（hopping constant）、與交互作用位能 U 這三個參數決定。原則上我們也可以讓單一個粒子在每不同節點上看到不同的位能值 V(x_i)，但這個項其實可以跟化學勢合併在一起，並且為了得到最初步的結果我們暫時不考慮這樣的複雜性。

Figure1.在玻色子的問題中，由於沒有不相容原理，並沒有一個軌域只能填一個粒子的限制，思考玻色問題基態的直覺一部分可由怎麼分佈會使得能量變低決定。（photo credit: 作者自繪）

對於理論物理學家們而言，給定這樣一個模型，我們並不奢望直接可以分析它的所有動力學性質，在少數的相對簡單的問題中，其中一個我們有希望能回答的是：這個模型的基態的「相」是什麼？在做任何計算之前，我們可以先看一些極限的例子，並嘗試定性地去推敲這些極限的相，接著用比較精確的定量分析來內插解析出是哪些相連接這些極限的例子。

讓我們看看第一個極限：U/t≪1 或 U=0。

在這個極限，玻色子們其實看不見對方，也就是說多粒子問題變回了單粒子問題，同時，我們有能力去計算單一個玻色子的能階，接下來要回答的，就是當有很多玻色子要填進這個能階時它們要怎麼分佈。對於自由的玻色子而言，這個問題的答案是已知的，因為它們不需要遵守庖立不相容原理，大家可以一起擠到最低的能態去，也因此，全部的人共享同一個波函數，這樣的物理相信有些讀者能夠心領神會，這也就是所謂的玻色愛因斯坦凝聚（Bose-Einstein condensation），也就是說，基態是個超流體（Superfluid）。

另外一個極限是 t/U≪1 或 U=0。

在這個極限中，玻色子們一但被放到某個節點上，就沒有移動的能力。要決定 N 個粒子的基態，等同於考慮要把這些粒子以降低能量為考量分配到所有節點上。讀者自己可以估計幾個簡單的粒子，比如把 2 個粒子分到 2 個節點上，或把 4 個粒子分到 2 個節點上。在第一個例子中，當兩個粒子在兩個節點上的時候，交互作用是 0 也因此能量為 0，但當兩個粒子放在同一個點上時，能量為 U。多看看幾個例子，大家很快便可以說服自己，當每個節點都有一樣數目的粒子，系統的能量最低。這種從能帶理論上看是導體，但因為交互作用失去導電性的狀態，我們稱為莫特絕緣體（Mott Insulator）。

因為戈登斯通玻色子（Goldstone Boson）的緣故，超流體是沒有能隙（energy gap）的，意思是我們不需要施加很大的能量才可以激發超流體的基態，另一方面而言，絕緣體是有能隙的，我們必須施加某個量值以上的能量才能把系統從基態帶到另外一個態，也就是說，從能譜的角度，這兩個基態在不同的物質相裡面，但因為它們屬於兩個極端的狀況，當 t/U 處於 0 和無限大中間某個值時，必然要存在一個相變化。

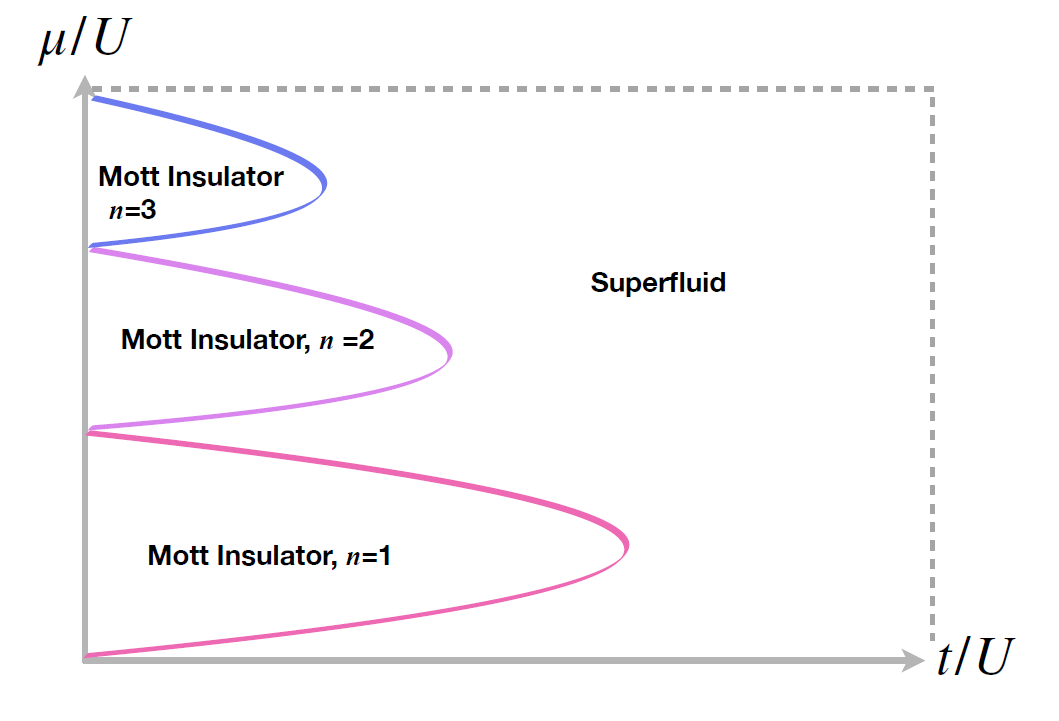
在進入下一個課題前，讀者們可以稍稍回顧，筆者前面在論述超流體和絕緣體這兩個相的存在時，基本上沒有進行什麼認真的計算，而是由考慮系統的某些極限，並透過更基礎一層的知識去判斷該有的結果。當然，更精確的相分佈還是需要透過計算得到。在圖 2 中，我們約略描繪了在平均場（mean field）的計算下，玻色 Hubbard 模型的基態根據給定的化學勢、躍遷常數與交互作用所處的物質相。

Figure2. 本圖中我們考慮不同的化學勢與躍遷常數下玻色Hubbard模型的基態物質相。（photo credit: 作者自繪）

目前為止，我們說明了本系統在兩個極限中的物質相，以及相變化的存在。對於理論物理學家而言，下一個問題就是往相變化的領域前進，研究這個系統的臨界現象（critical phenamonon）要妥善寫下精確描述這個範圍物理的模型是比較技術性的，我們不會鑽入詳細的量子場論分析，但我想要陳述一個問題，並畫出量子理論計算出的結果。

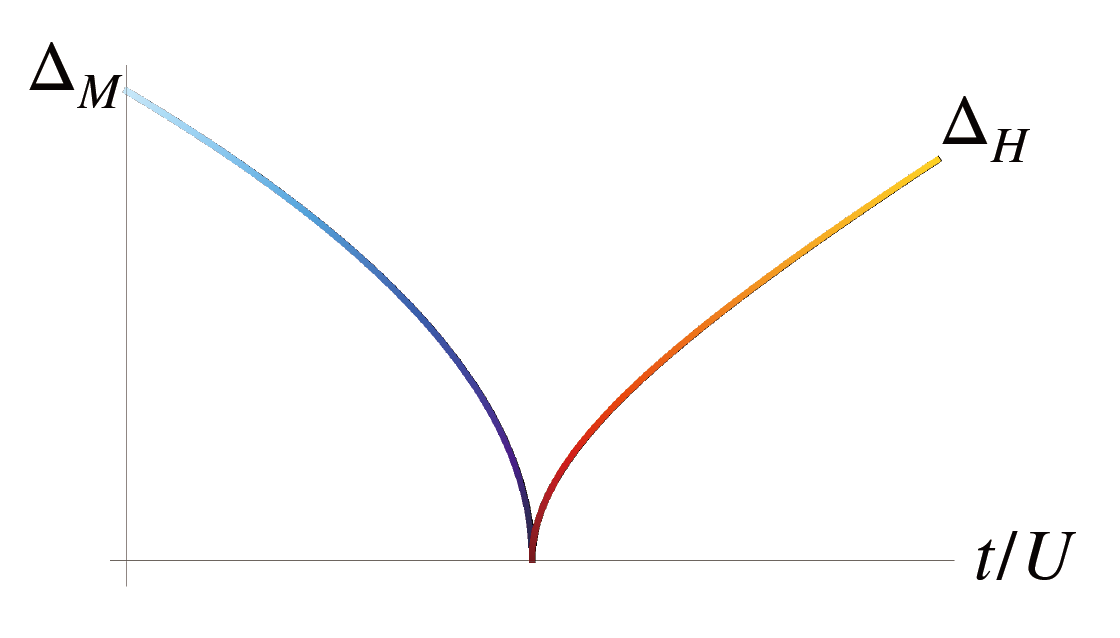
首先一個我沒有證明的事實是，這個臨界點的有效理論被認為是一個「相對論性」（relativistic）的理論，因而在超流體態中，我們除了有無質量的戈德斯通粒子，接近相變化時，還會獲得另一個有質量的（類比的）^[1]「希格斯玻色子」（Higgs Boson）。因為這是超流體的一個特徵，我們相信這個希格斯玻色子的質量 ∆_H 在接近相變化的時候會越來越小，並且在臨界點時為 0。另一方面而言，在莫特絕緣體的相中，我們也有一個能量尺度是絕緣體的能隙 ∆_M，因爲這個能隙是絕緣體的特徵，我們也期待在接近相變化時，這個值會愈來愈小，並在臨界點為 0。

實際的計算被呈現在圖 3 之中。但更引人入勝的是，這樣的計算結果目前已經被冷原子實驗實現 [3]，被認為是在非基本粒子實驗中尋獲的希格斯粒子。

在本文中我們討論了簡單的玻色 Hubbard 模型，並用物理的論述討論了基態所處的物質相。我們也呈現了在相變化附近的計算結果，而這些結果不只是理論上的宣言，同時也已被實驗所驗證。