v=5/2 量子霍爾態之謎(下)
■誰是描述 v=5/2基態的波函數?Pf, aPf, 還是其他的可能性?
撰文|蕭維翰
在前兩篇文章中我們首先複習了量子霍爾效應,指出v=5/2的特別之處,並且對於v=5/2 的其中一個強力候選波函數 —— Pf 態進行了一些定性上的介紹。我們也指出,Pf 態所內建有趣的數學性質,也間接反饋到實驗的研究,強化了人們對真實系統v=5/2量子霍爾態的興趣。
在本文中,我們將討論現今與 Pf 分庭抗禮的候選人(們)。
首先讓我們回憶,在本系列第一篇文章中的一個等式
v=5/2=2+1/2
這個分解的意思是,在理論研究上,我們常常把這個態分解成兩個全填滿的蘭道階與一個半填滿的蘭道階。倘若蘭道階之間的交互作用可以省略,我們則可以把所有的物理投射到一個半填滿的蘭道階,這個問題在形式上就會接近其他在最低蘭道階的量子霍爾效應問題。
經過這樣的簡化,我們觀察到,如果這個態基本上就是一個 v=1/2態,那這個問題具有粒子-電洞對稱(particle-hole symmetry)。粒子-電洞轉換等同於把所有佔滿的軌域換成空軌域,並把空軌域填上電子。回憶一下v的意義就是被佔滿的軌域與空軌域的比值,粒子-電洞作用的方式是:
![]()
也因此v=1/2在這個操作下應該回到v=1/2。
然而,如果我們真的寫下 Pf 波函數的數學形式,然後將所有電子跟電洞的座標對換,我們並不會得到原來的波函數,這個新波函數稱作 anti-Pfaffian [1, 2],或簡寫成 aPf 。但由於在單一蘭道階的模型是符合這個對稱性的,也就是說,從檢測最低能量的角度,我們無法分辨這兩個波函數。
從觀測科學的角度,在深入追究兩者之前,我們應該先問,那麼實際上的半導體,蘭道階之間的影響是否能省略呢?答案是否定的。尤其在計算中考慮其他蘭道階時,模型中會產生一些三體交互作用的項,這個項直接破壞了粒子-電洞的對稱,也因此在真實世界中,其中一個波函數會有較低的能量。
讓我們梳理一下至今的邏輯。在考慮v=5/2的問題時,因為其他蘭道階的效應太複雜,我們首先只專注於其中v=1/2填滿的部分,嘗試找出它的基態,然後再釐清將其他蘭道階放回來時造成的修正。然而,在v=1/2的蘭道階上,因為粒子 - 電洞對稱性,若 Pfaffian 波函數在能量的角度上有機會成為基態,那麼在同樣的精確度下,anti-Pfaffian 也有機會。接著,考慮其他蘭道階,當一些破壞粒子-電洞對稱的項進到問題中,這兩個狀態的波函數將具有不同的能量,那問題就是——誰有比較低的能量?
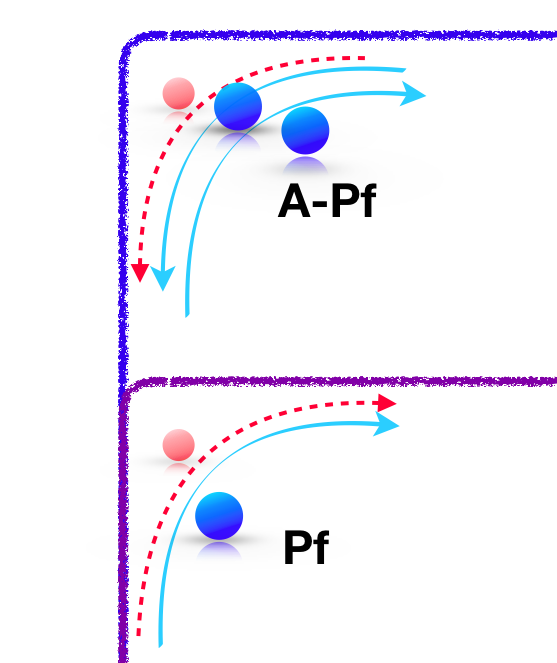
除了 anti-Pfaffian,在 2015 年,芝加哥大學的 D. T. Son 在其狄拉克複合費米子 [3] 的文章中指出,如果讓狄拉克複合費米子以 s 波形成古柏對,則這樣的配對自動是粒子-電洞對稱的,也因此不能是 Pf 或 aPf,而他將這個狀態稱之為 PH-Pfaffian。
目前數值計算還不足以讓我們下最終的結論(可以參見文 [4] 的引言部分。)但從計算基態能量的角度,結果通常是 Pf 或者 aPf。
物理學家們的下一個問題是,那有沒有一個關鍵的差異,讓我們可以從實驗上去分辨大自然比較鍾意的基態?
答案是肯定的。儘管這幾個波函數都具有一樣的電性 v=5/2、一樣的準粒子電荷e=1/4但如果我們考慮系統的邊界,並測量他們的霍爾熱導率,就會獲得不一樣的答案。以 ![]() 為單位,這三個狀態分別有—
為單位,這三個狀態分別有—
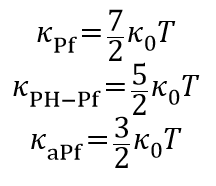
在 2017 年底,以色列 Weizmann 科學研究院的團隊提出的他們的測量結果 [5,6,7],就當大家認為 7/2 或 3/2 之謎就要水落石出時,該論文的結論是:他們看到了 5/2。
這當然不是說答案就是 PH-Pfaffian,但這無疑對理論物理學家們拋出了新的挑戰。如果 Pf 跟 aPf 能量上是比較受系統青睞的,那沒有其他的機制,在以 Pf 或 aPf 作為計算的出發點,卻也能夠得到 5/2 的係數。
在這兩年有幾個團隊考慮了真實系統中雜質與亂序(disorder)對於基態選擇可能造成的影響 [4,6],並且得出在某些條件下,因為亂序的存在 PH Pf 有可能出現在相圖(phase diagram)的某一個角落。然而,截至今日這個問題還沒有一個公認的答案,不同團隊提出的相圖也不盡相同。
約兩個月前,甫退休的哈佛大學教授 B. I. Halperin 在芝加哥大學以「What happens to the 5/2 state?」演講,也結論我們目前依舊無法斷言。但另一方面而言,實驗上出乎意料的結果,也是激發後續研究點子的契機。
參考資料:
[1] M. Levin, B. I. Halperin, and B. Rosenow, Phys. Rev. Lett. 99, 236806 (2007).
[2] S.-K. Lee, S. Ryu, C. Nayak, and M. A. Fisher, Phys. Rev. Lett. 99, 236807 (2007).
[3] D. T. Son, Phys. Rev. X 5, 031027 (2015).
[4] C. Wang, A. Vishwanath, and B. I. Halperin, arXiv: 1711.11557 (2017).
[5] M. Banerjee et al, Nature 545, 75 (2017).
[6] M. Banerjee et al, arXiv: 1710.00492 (2017).
[7] D. Mross et al, arXiv: 1711.06278 (2017).
--
作者:蕭維翰,臺大物理系畢業後逃到芝加哥,吹風吹雪之餘,做研究讀博士班。可惜離開臺灣後無海可看,只能在密西根湖旁揀一方堤岸,偽裝成看海的人。科教中心特約寫手,從事科普文章寫作。
