非厄米系統
■厄米對稱(Hermitian)存在於大部分的量子理論之中,但它卻不是必要的。如果放棄這個對稱性,系統將出現奇妙的物理現象和有趣的應用。
 撰文|陳奕廷
撰文|陳奕廷
薛丁格方程式是量子力學的核心,方程式裡面主要由兩個部分組成:哈密頓算符(Hamiltonian)和波函數。哈密頓算符決定於系統環境,而波函數包含所有關於量子態有用的資訊。對於一個特定的系統,我們把系統特性寫進哈密頓算符中,薛丁格方程式就會告訴我們這個系統中的波函數長什麼樣子。
通常,物理學家會要求哈密頓算符滿足一些基本的數學條件,以滿足大自然中對稱性,例如;量子態的能量是實數、粒子數和能量守恆等。這些基本的數學條件被稱做厄米對稱性(Hermitian)[註1],幾乎所有的基礎量子理論都建立在哈密頓算符是厄米對稱的前提下。本篇文章介紹如果不要求厄米對稱,量子理論會出現的奇異現象和有趣應用。
●獨特點(Exceptional Point, EP)
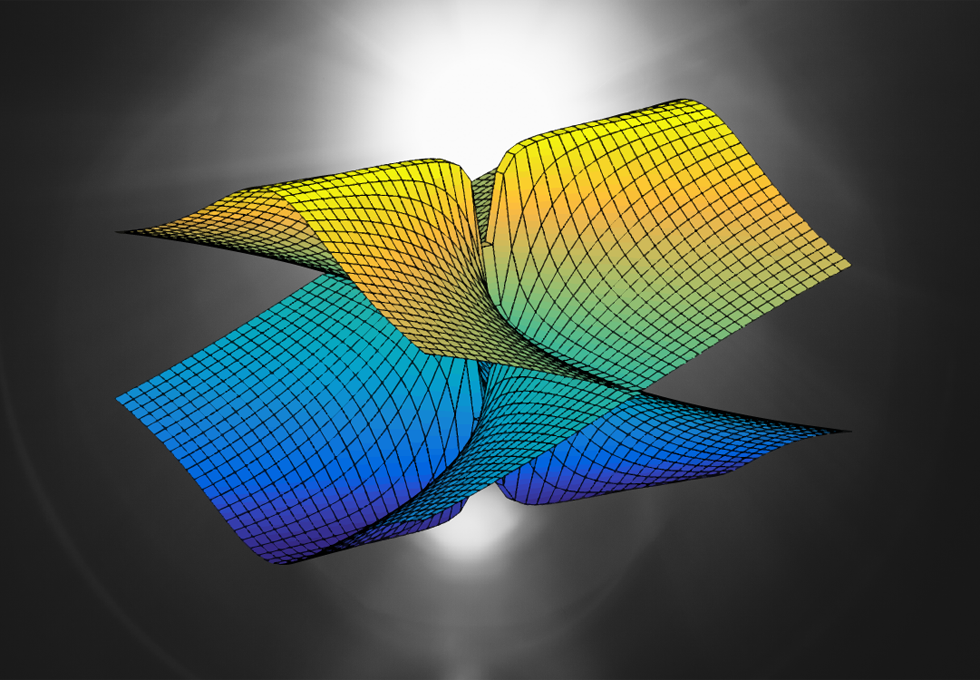
在非厄米系統中,最奇異的特性是「獨特點」的存在 [註2]。一般的量子系統中,不同的量子態處於相同的能量是一件極為普通的事情,例如:苯環的共振結構。儘管能量相同,苯環的共振確確實實是由「兩個」量子態組成。但在獨特點上,多個量子態除了具有相同的能量,它們融合成為「一個」量子態。

圖一是量子態在厄米系統和非厄米系統的結構,厄米系統隨環境變化非常的平整緩慢。而非厄米系統,在特定的系統參數下(綠色箭頭)量子態糾結成一團、並且融合。物理學家提出很多理論,描述獨特點在電子結構中潛在的應用。但是電子這樣的費米子(fermion)必須要滿足實數能量和粒子數守恆,難以應用在非厄米系統中。相較之下,光子是一個波色子(boson),它能任意地被產生或是消滅,也可以有虛數能量 [註3],是實現厄米系統非常好的候選人。以下來看一些「獨特點」的應用。
●量子態切換器
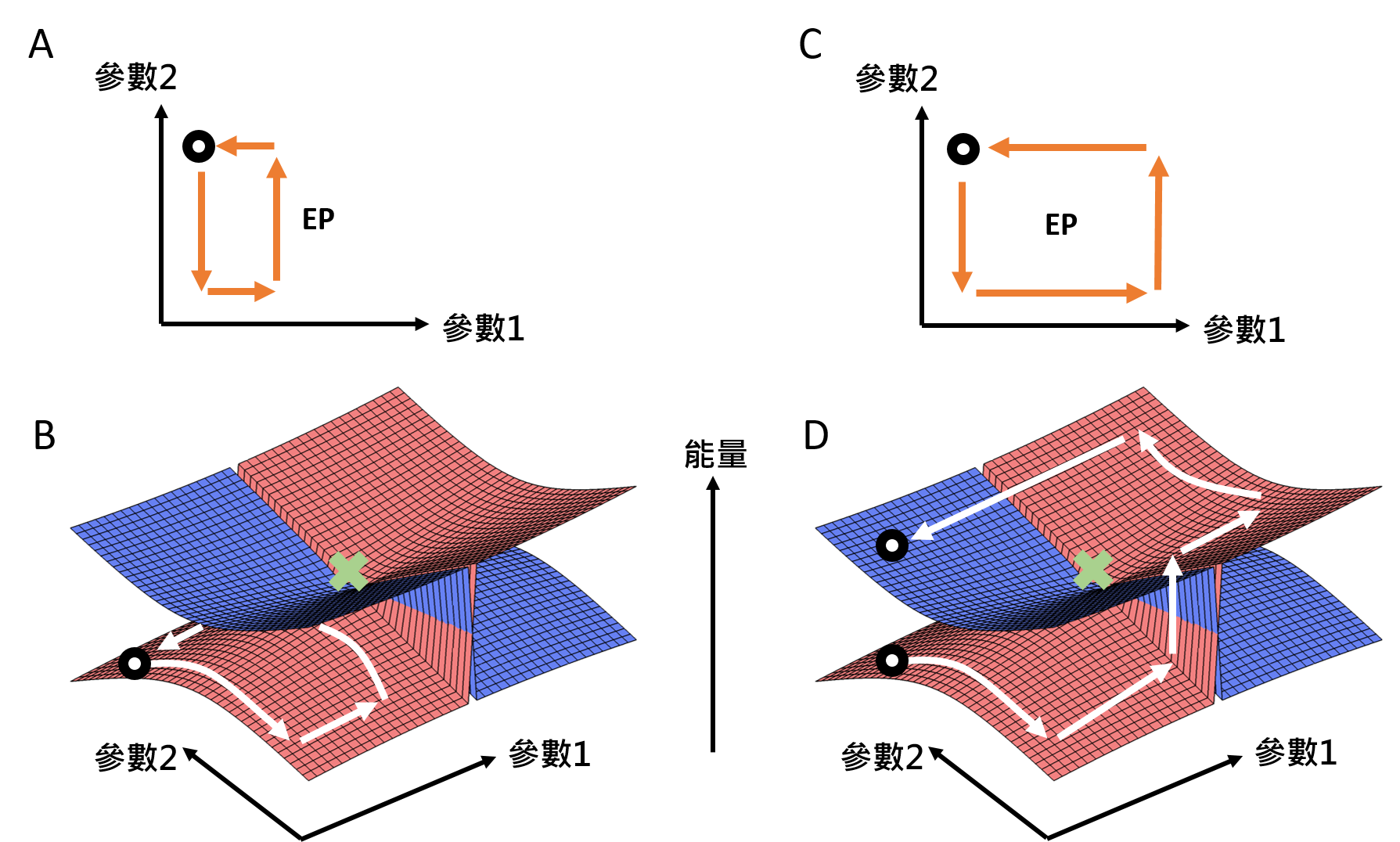
量子態的能量隨系統環境變化,在獨特點上,兩個量子態融合成一個(圖一右的綠色箭頭處)。而在獨特點附近,量子態的變化非常奇異。如果我們設計一個實驗,控制系統中兩個參數,使系統環境在參數空間內走圖二A的封閉路徑,量子態會走如圖二B所示的路徑(白色箭頭),它會回到原來的狀態。但如果像圖二C那樣包含一個獨特點(EP)的封閉路徑,量子態會從紅色的變成藍色的。科學家發現,如果包含獨特點封閉路徑是逆時針的,量子態都會變成藍色的,而順時針都會變成紅色的。
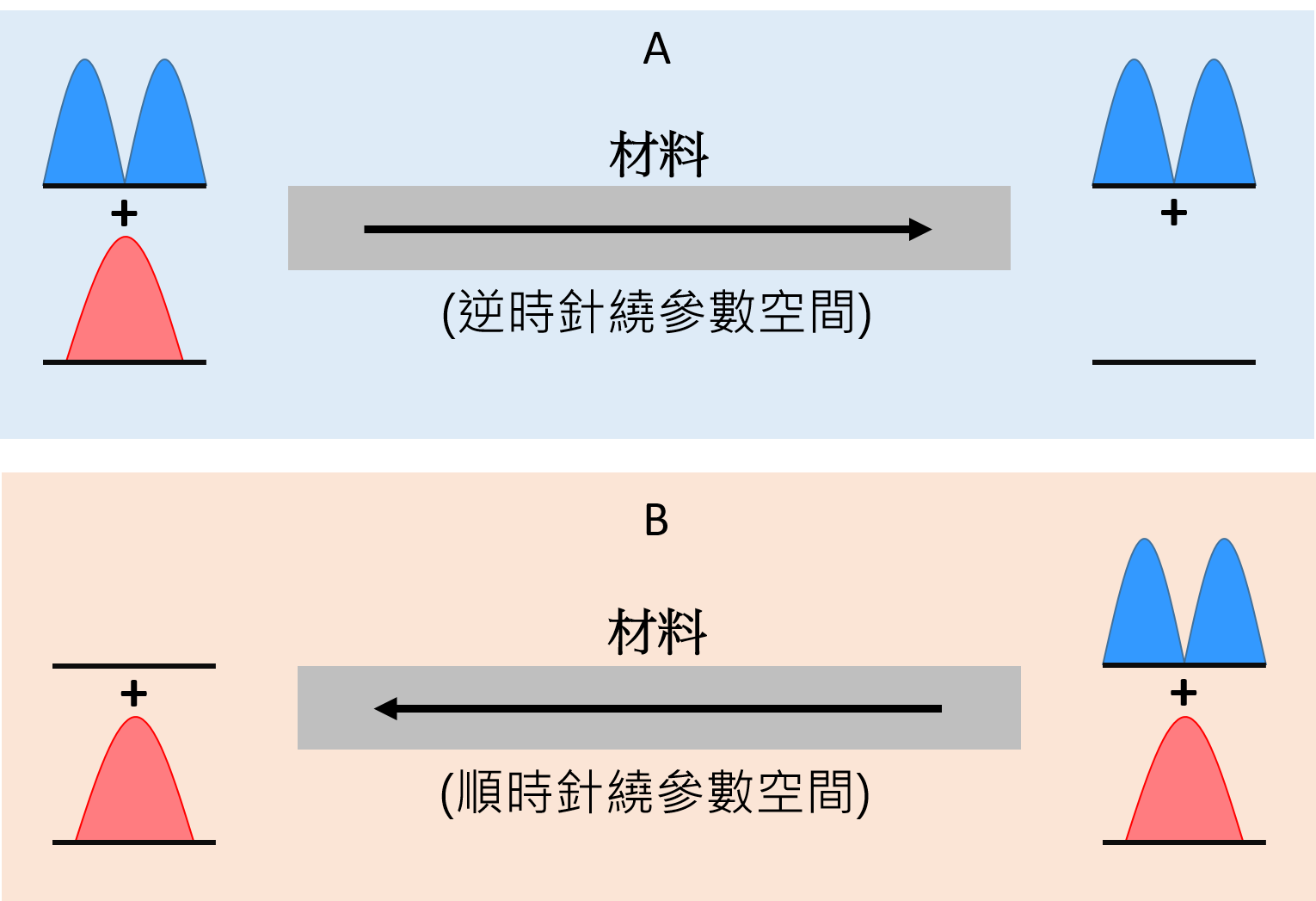
如果你發現上述的理論細節很難理解,來看看實際應用。科學家設計一種材料,材料內不同位置有不同的性質。當光子從左邊穿越材料到右邊時,光子就像是經歷了圖二C和D中的逆時針過程;從右邊到左邊,則是順時針過程。如圖三所示,無論是光子本來處於紅色或藍色的量子態,向右傳輸後,所有的光子都跑到了藍色量子態(圖三A)。相反地,向左傳輸,光子都跑到紅色量子態(圖三B)。這個現象除了反直覺又很酷之外,在單一元件內達到兩種量子態的控制切換,對光電路也有很大的應用。
●高敏度偵測器
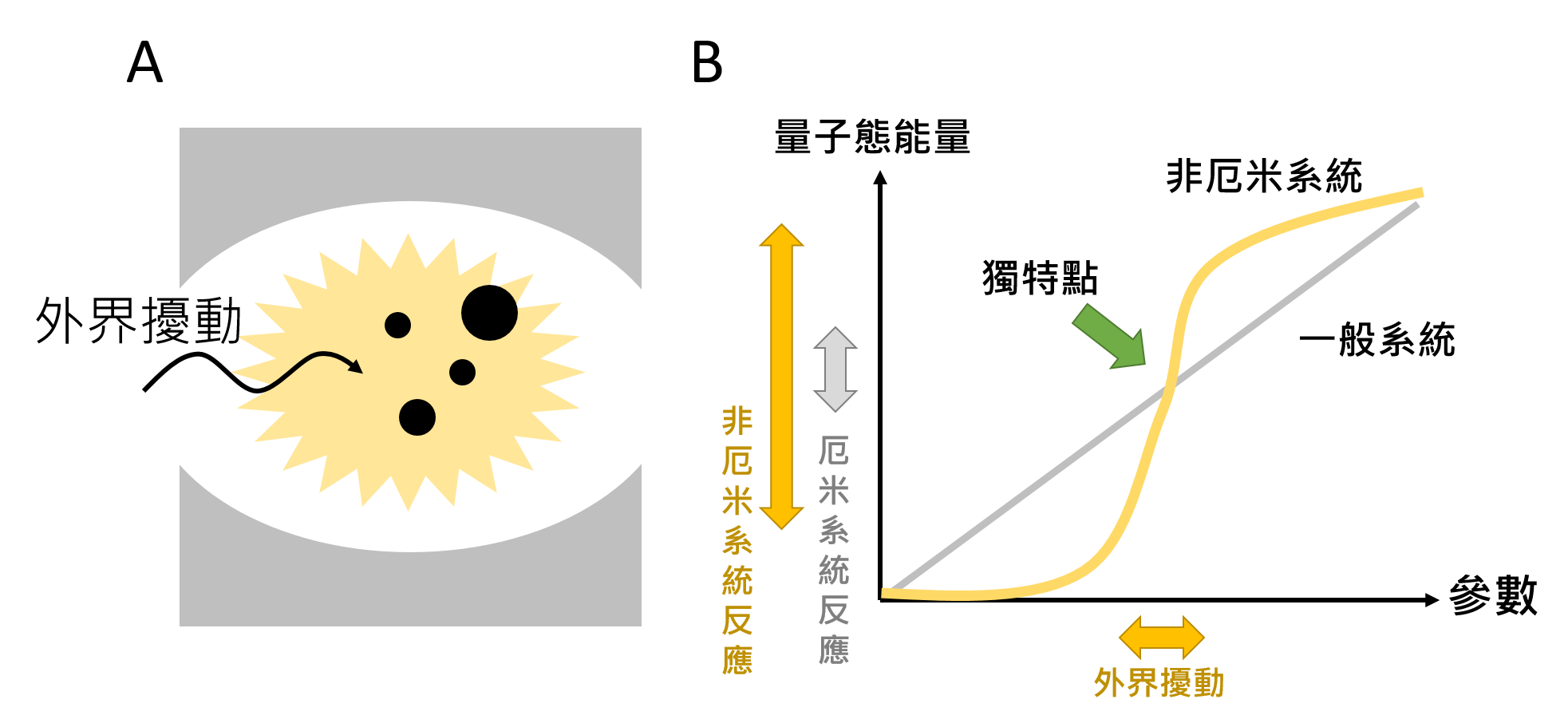
上面曾經提到在獨特點附近量子態的能量變化非常劇烈,科學家將這個特性應用在偵測器中。系統受到外界干擾時(例如有原子或分子經過),系統環境會出現變化,這個變化也會反應在量子態的能量中。但通常這個變化非常微小,難以被測量。但在一個非厄米系統中,獨特點對參數變化非常敏感。如圖四B所示,微小的擾動(橫軸橘色雙箭頭),對厄米系統來說是微不足道(縱軸灰色雙箭頭),但在非厄米系統中卻造成非常大的反應(縱軸橘色雙箭頭)。
透過這個原理製造的感應器非常靈敏。這樣的裝置靠的是對底層物理的了解加上材料的設計,結構相對簡單。也因為不須要複雜的機構,它在奈米尺度下的電路應用非常有潛力。
附註:
[註1] 厄米對稱指的是在共軛(conjugate)和轉置(adjoint)運算下守恆。
[註2] 英文為exceptional point,筆者譯為「獨特點」,也可以翻譯為「優越點」、「例外點」等。
[註3] 光子理論中,實數能量代表光的頻率,虛數能量代表光子被吸收或耗散的速率。
參考資料:
- Hossein Hodaei et al., Enhanced sensitivity at higher-order exceptional points, Nature 548, 187 (2017)
- Weijian Chen et al., Exceptional points enhance sensing in an optical microcavity, Nature 548, 192 (2017)
- Jörg Doppler et al., Dynamically encircling an exceptional point for asymmetric mode switching, Nature 537, 76 (2016)
- H. Xu et al., Topological energy transfer in an optomechanical system with exceptional points, Nature 537, 80 (2016)
--
作者:陳奕廷,台大物理系學士,史丹佛大學應用物理系博士班就讀中。
