RSA加密法遇上量子電腦

■通訊和情報一直是商業和國防最重要的一環,而加密是其中的核心。二十世紀末以來, RSA加密法憑藉著古典電腦難以企及的複雜度變得日趨流行,安全性高。但對於特定的計算工作,量子電腦的計算力遠遠超越古典電腦,這是否會對你我日常都在使用的RSA加密造成威脅呢?回答問題前,先讓我們看看RSA和量子電腦背後分別有些什麼。
撰文|陳奕廷
●在RSA之前:對稱性加密
關於對稱性加密,最廣為人知的是二次大戰中德軍的密碼系統「Enigma」。每位軍士官擁有一份密碼表(金鑰),當收到加密訊息時(圖一),必須用相同的密碼表才能翻譯密文。敵軍竊聽者缺少了密碼表,就算攔截到訊號也無法解開密文。這種密碼系統非常成功,當時德軍靠著它,透過閃電戰順利擊敗周圍國家。
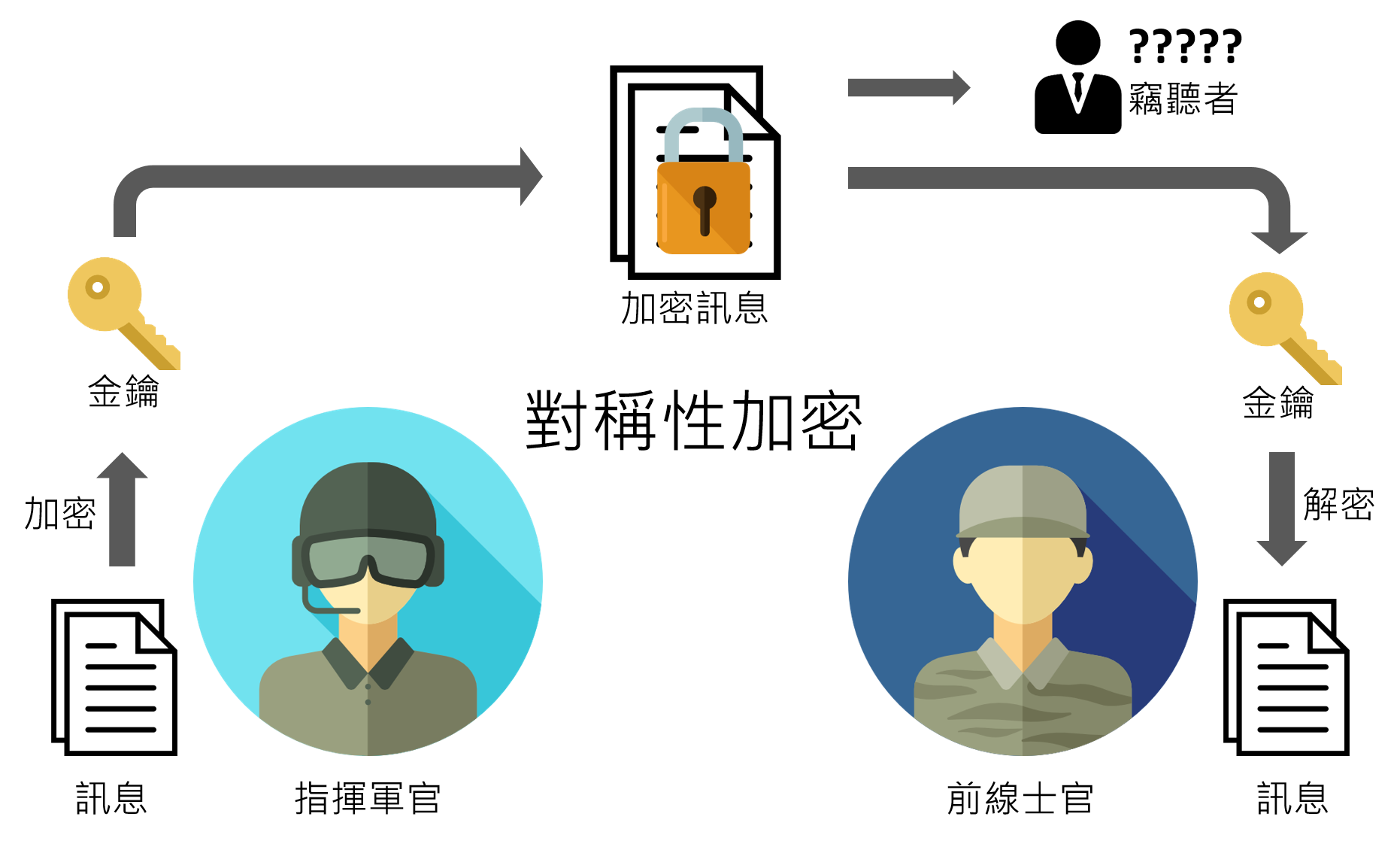
●非對稱性加密
德軍將密碼表印在水溶性材料上,每個月更新一次。若遭到俘虜,密碼表可以立即被銷毀。即使密碼表真的被拿走,也只能用一個月而已。但這仍非完美,如果團體中有間諜定期外流密碼表,密碼系統就瓦解了。可能的對策是每兩個人之間都有一份獨特的密碼表,若團體中有n個人,一個間諜外流的密碼表不會影響到其他(n-1)人。但如此一來,團體總共需要約n平方組密碼表[註1],非常不方便。再者,要和一位新成員秘密通訊,如何安全傳遞密碼表也是一個大問題。針對這些難題,非對稱性加密因應而生。
非對稱性加密的精隨在於加密和解密需要不同的鑰匙,分別為公開金鑰和私有金鑰。任何擁有公開金鑰的人都可以加密任何訊息,但唯有私有金鑰才能解開密文。圖二中,男孩為了安全地向女孩發送訊息,事先向女孩索取一份用來加密的公開金鑰。女孩收到加密訊息後用私有金鑰解密。若有竊聽者攔截訊號,他也只能得到已加密的訊息和加密用的公開金鑰,無法解密。值得一提地,若男孩誤刪自己的訊息原文,他本人也無法透過公鑰還原訊息,地位變得和竊聽者一樣。這樣的密碼架構下,雖然需要花時間事先索取公鑰,但免去了傳送密碼表的風險,安全度大幅提升。
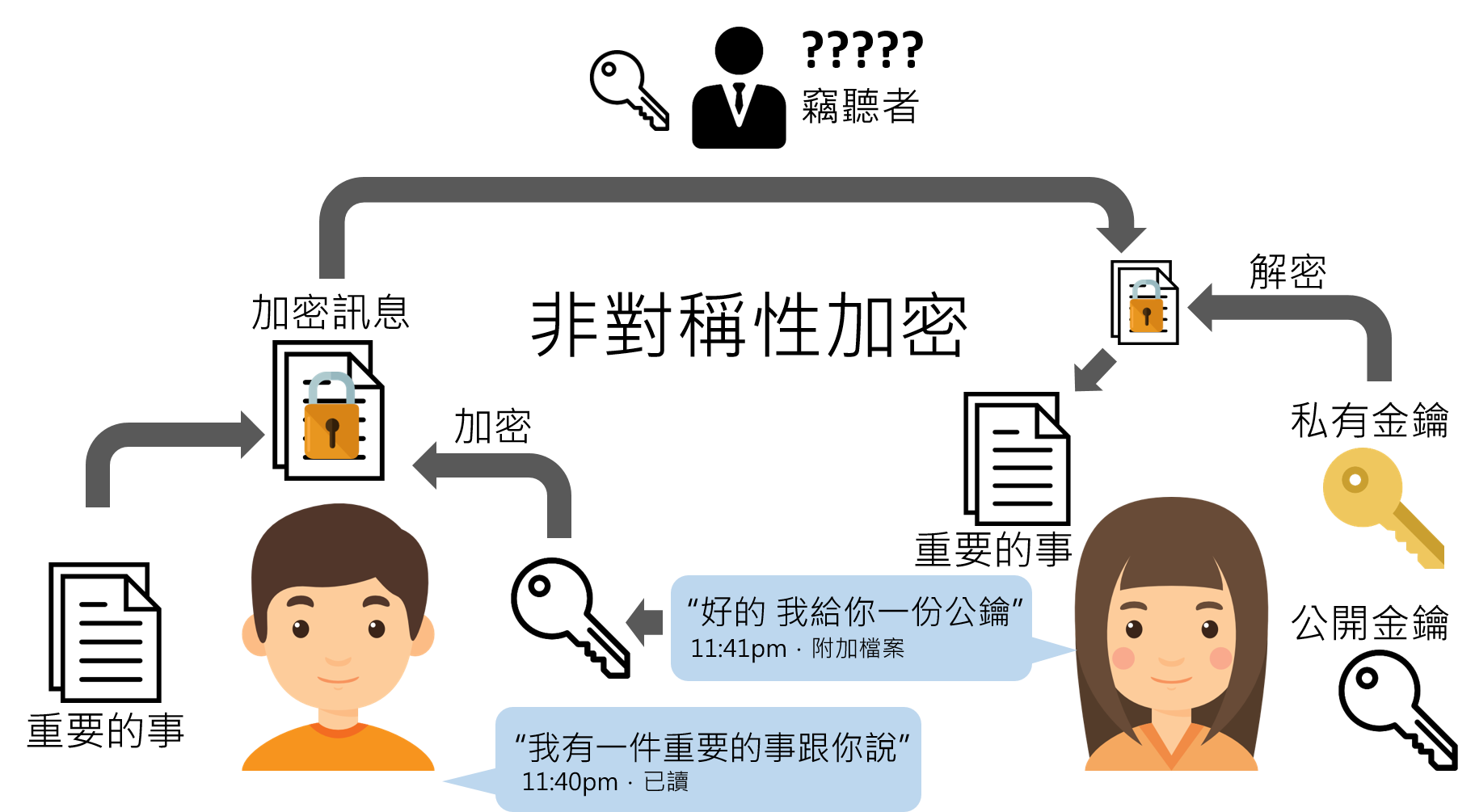
●密碼背後的數學和安全性
當今最廣為使用的非對稱加密法是RSA演算法,其名稱由發明者Ron Rivest、 Adi Shamir 和 Leonard Adleman的姓氏組成。概念如圖三,RSA算法基於兩個質數p和q,它們製造符合條件的公開金鑰(n,e)和私有金鑰(n,d)。 加密和解密是對訊息取次方並取餘數(mod) [註2],例如要使用公鑰(n=143,e=7)加密體重「72」公斤,讀者動筆 (或計算機) 算算會得到密文 。解密時,用私鑰對密文做類似的運算可以得到 。
對於沒有私鑰卻想要破解訊息的竊聽者,他唯一的資訊只有公鑰(n,e)。其中一種破解方式是對n做質因數分解找出p和q,從而推導出私鑰d。但是對於標準的2048位元RSA加密,就算用目前世界上最強的超級電腦(太湖之光,中國製),花費地球年齡的時間(46億年)都無法破解。RSA演算法安全性高,又只需分享公開金鑰,因此從社交軟體到軍事通訊都有他的蹤影,我們的生活可說是一舉一動離不開RSA。
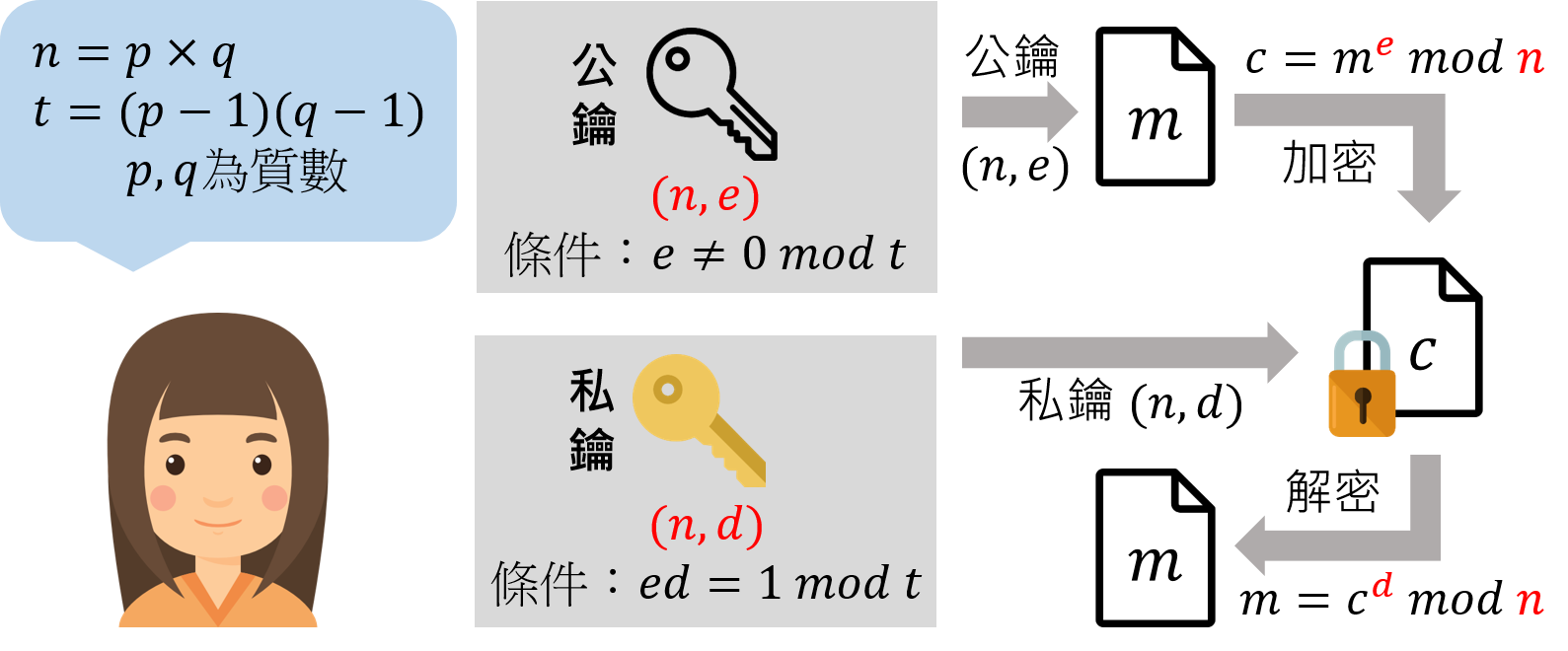
●量子電腦和週期性
量子電腦針對特定的問題,計算能力遠大於古典電腦。由於量子力學用「波動性」的概念來描述物質,波動的「週期」是量子力學中根本的性質之一。各種物理量之間存在共軛性,而這些共軛的物理量有像是波動和週期的相互關係。例如:動量可以想成是空間上的周期、能量像是時間上的周期,或更抽象地,粒子數像是相位中的周期。因為這些特性,量子電腦特別擅長尋找週期。
在上述RSA算法中,一個核心的元素是「取餘數(mod)」。這個函數具有週期性,是他的優點也是他的弱點。因為有週期性,他可以有效率地被用於加密和解密。但是若有一台機器能夠快速找出函數的周期性,RSA算法則能輕鬆地被破解[註3]。量子電腦恰好就是這樣的機器,破解RSA算法是量子電腦發展的目標之一,也是學界、業界和政府投入大量資金進行研發的重要原因之一。
若要破解一組2048位元的RSA加密,理論上大約需要4000個量子位元(qubit)。目前Google和IBM的量子電腦約有20個量子位元。儘管數量仍遠遠不足,但是相較於2016年的9位元和5位元,兩家公司都將數目提升兩倍了。未來能否用量子電腦對現有密碼系統革命,讓我們繼續看下去吧。
註釋:
[註1] 團體中有n人,任兩個人配一個獨特的密碼表,總共需要n(n-1)/2個,複雜度為n平方。
[註2] mod是取餘數的意思,他的格式為「被除數 = 餘數 mod 除數」。例如17除以5等於3餘2,可以寫作「17=2 mod 5」。
[註3] 最廣為人知的破解RSA的演算法是「秀爾演算法(Shor’s Algorithm)」,對細節有興趣的讀者可以參見其維基百科條目。
參考資料:Eleni Diamanti et al., Best of both worlds, Nature Physics 13, 3–4 (2017)
--
作者:陳奕廷,台大物理系學士,史丹佛大學應用物理系博士班就讀中。
