旋轉的玻色愛因斯坦凝聚態
撰文|蕭維翰
高中的物理課程中,我們學習動量、角動量,用這兩個量來量化一個物件平動狀態以及轉動的狀態。儘管大多數人在大學後不會再接觸更進階的物理課程,但事實上就描述運動狀態而言,也沒有更多新的物件了。
物理學的理論描述是盡量得跟實驗呼應的,也因此,即便是今日大如強子對撞機的尖端實驗,源頭的想法也都是想藉由動量、角動量等在交互作用的前後關係,去獲得物理資訊。
本文就來略談,當我們轉動一個流體,更精確地說,一個玻色愛因斯坦凝聚態(Bose-Einstein Condensate),什麼事情會發生。
首先,讓我們稍稍複習一下玻色愛因斯坦凝聚態是什麼。在探索「沒有人懂得量子力學」一期中,我們得知了在量子力學的層次上,(3+1 時空內的)粒子可區分為兩種,一種叫做玻色子(Boson),另一種是費米子(Fermion)。他倆最大的差異是,在一個多體的波函數內,兩個同樣[1]玻色子角色互換,波函數是對稱的,而兩個同樣的費米子角色互換,波函數獲得一個負號。從這個定義可以得到一個立即的結論,如果我有一堆一樣的費米子形成一個多體的物理態,在這堆費米子內,每個人都要佔據不一樣的單粒子態。然而,玻色子們並不介意彼此佔據一樣的狀態,從而在低溫時,大多數的玻色子都會進入到能量最低的基態(ground state)形成一個凝聚態(condensate),這裡頭的玻色子共享一個巨觀的波函數。
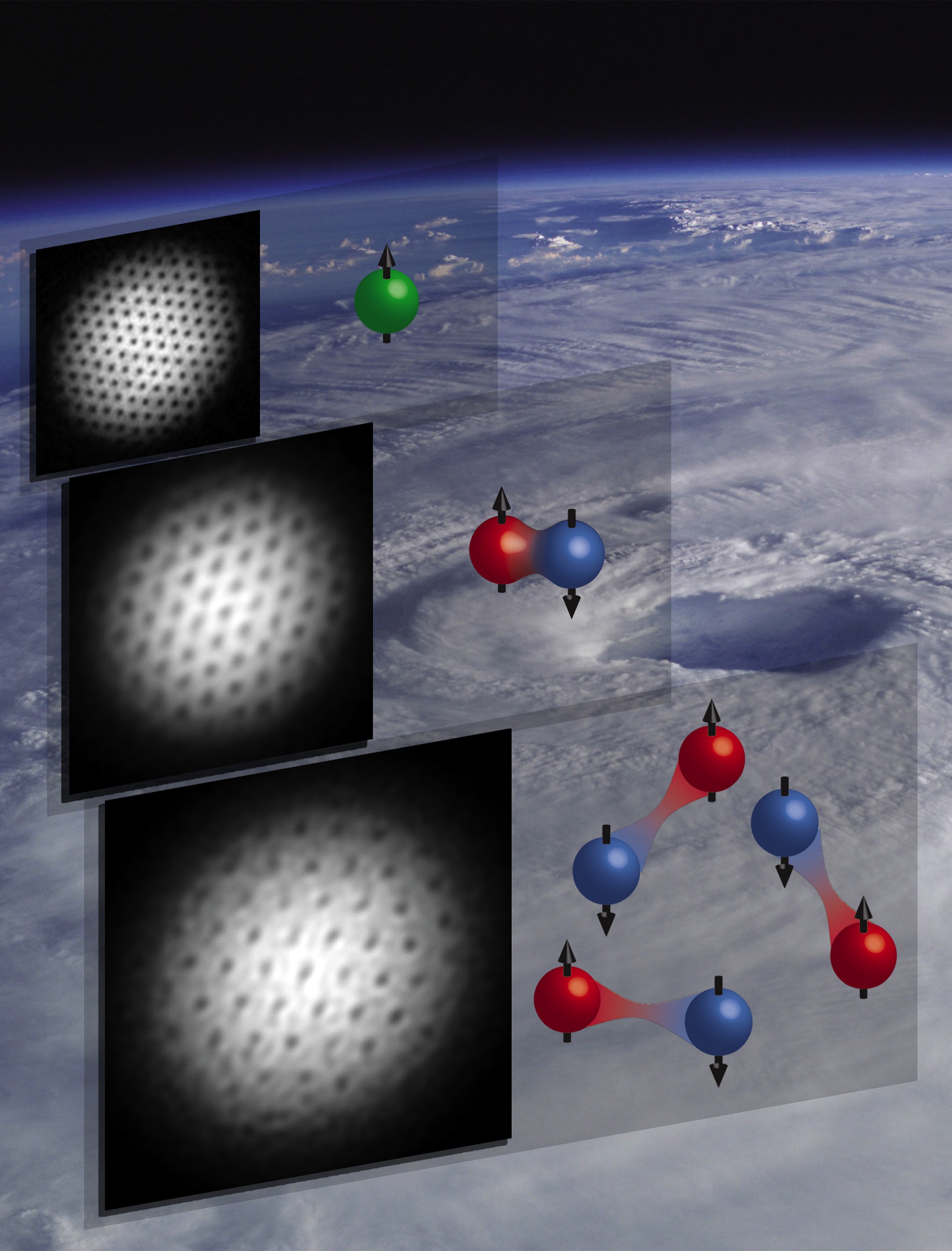
再來我們說明旋轉一個流體會發生的事。更明確地說,我們旋轉一個在侷限在3 維空間某個區域內的流體。[2]對於轉動一個流體的物理結果,不需要知道任何量子力學,便能有一個粗略的想像:因為離心力的關係,整個流體會沿著旋轉軸的方向變扁平。另一個可能性可以藉由攪拌早餐的咖啡來想像,當攪動快到一個程度,在咖啡中會有漩渦產生。

遠在 1960 年代或更早,人們便開始針對 4He、3He (氦的不同同位素)進行類似的研究,並且也觀察到漩渦的組態。4He 是玻色子,在低溫時形成超流體,但它卻只有約略 10 % 的粒子會進入愛因斯坦凝聚態(這是一個至今都困擾物理學家的難題。)直至 1990 年代冷原子物理實現高比例的玻色愛因斯坦凝聚[3]後,實驗端才真正獲得了研究這類問題的可行性。
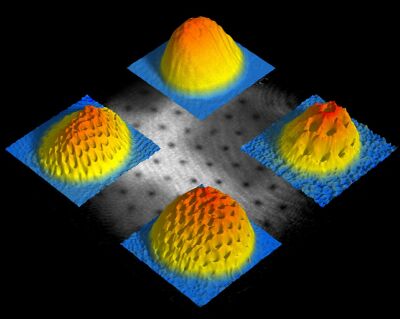
在理論端,物理學家也有能力指出在一個簡諧位能井[4](harmonic trap)中,根據轉動的角速度大小,我們可以觀測到以下的現象:(1) 中轉速時,一個或少個漩渦產生,可以觀測到漩渦進動的現象。(2) 高轉速時,由於離心力,整個系統已經等效於一個 2 為系統,可以觀察到許多漩渦的產生,並且這些漩渦並非隨便排列,而是形成一個晶格(lattice)。(3) 在更高轉速時,整個玻色愛因斯坦凝聚態會被破壞,新的基態是一個強關聯的多體量子態,而不是一個巨觀的相干態。(coherent state)
就筆者所知,(1)、(2) 已經在實驗上被看見,但要達到階段 (3) 的轉速,技術上仍有問題要克服。[5]
最後筆者從自己的角度,說明為何人們對這類問題有興趣,一部分原因如下:(i)隨著轉速提高、漩渦數的增加,描述系統適當的元素其實從粒子逐漸轉變為漩渦。(ii) 這所導致的是原本所有粒子喜歡待在玻色愛因斯坦凝聚態裡,共享一個巨觀的波函數,但當漩渦變成主角後,這個傾向就被破壞了,新的基態裡便沒有玻色愛因斯坦凝聚態,這是一個「相變化」(phase transition)。(iii) 此外在階段 (2),漩渦們是形成一個晶格,但在階段 (3),理論學家預測這是一個液體態,亦即從階段 (2) 到 (3),存在著所謂「漩渦晶格熔解」的相變化。(iv) 旋轉的物理在形式上跟磁場是很相近的,而一個 2 維系統放在強磁場中,就是量子霍爾效應的平臺,事實上在階段 (3) 的強關聯基態就跟霍爾效應系列中勞夫林波函數(Laughlin wave function)很類似,在克服轉速極限的困難後,或許可與霍爾物理的圈子互通有無。
「旋轉」是一個大家都能理解的操作,但透過旋轉玻色愛因斯坦凝聚,我們依舊看到了一些超乎預期的物理以及觸類旁通,瞭解其他問題的可能性。
Reference:
[1] A. L. Fetter, Rotating trapped Bose-Einstein Condensates, Rev. Mod. Phys. 81, 647 (2009).
[2] L. P. Pitaevskii, and Stringari, Bose-Einstein Condensation, Oxford University Press (2003).
[3] B. P. Anderson, Phys. Rev. Lett. 85, 2857 (2000).
[4] N. R. Cooper et al, Phys. Rev. A 70, 033604 (2004).
Photo courtesy to professor Wolfgang Ketterle and his lab at MIT. http://cua.mit.edu/ketterle_group/home.htm
註解:
[1] 這裡的「同樣的」意思是說他們是同一種類的粒子,譬如兩個光子,或兩個電子。
[2] 就像火影忍者裡的螺旋丸!
[3] 1995 年,在UC Boulder 的Eric Cornell 和 Carl Wieman使用 Rb 原子完成。
[4] 表示用來侷限玻色氣體的位能是跟簡諧運動一樣的位能。
[5] 這資訊有點老,我不太清楚 2009 至今的實驗進展。
--
作者:蕭維翰,臺大物理系畢業後逃到芝加哥,吹風吹雪之餘,做研究讀博士班。可惜離開臺灣後無海可看,只能在密西根湖旁揀一方堤岸,偽裝成看海的人。科教中心特約寫手,從事科普文章寫作。
