【大宇宙小故事】23 同名同姓又同源
撰文|葉李華
十七、八世紀的瑞士,出現一個顯赫的「數學家族」,三代間產生了八位優秀的數學家,至今仍是世界紀錄。
然而令人費解的是,這個家族的名字經常一再重複。比方說,第二代中有兩個同名同姓的堂兄弟,兩人都叫尼古拉‧伯努利。後世學者為了避免混淆,只好替他們加上編號,於是在數學相關文獻中,他們的名字通常是這麼寫的:
Nicolaus I Bernoulli(1687-1759); Nicolaus II Bernoulli(1695-1726)
由於他們是平輩,所以編號就是編號,不能解釋為「一世」和「二世」。如果將這兩個名字翻譯成中文,恐怕只能譯為尼古拉‧伯努利一號與二號,沒有別的選擇。
至於大家所熟悉的柏努利原理,發現者丹尼爾‧伯努利(Daniel Bernoulli, 1700-1782)是尼古拉‧伯努利二號的弟弟。這位丹尼爾比較幸運,沒碰到同名的平輩。雖說他有個姪兒也叫丹尼爾,但既然是晚輩,稱之為丹尼爾‧伯努利二世也勉強說得通了。
總而言之,「同名同姓」和「同出一源」兩件事如果碰在一起,保證會造成困擾,應當盡量避免才對。
偏偏在數學文獻中,「黎曼幾何」這個名詞就有類似的尷尬處境,它有兩種不同的意義,源頭都是黎曼於1854年發表的一場演說。就非歐幾何學而言,黎曼幾何是橢圓幾何的同義詞;而在微分幾何學的領域,黎曼幾何另有相當不同的意義。
不過,如果想要避免誤會,其實也是舉手之勞。

(圖像來源:維基百科)
●黎曼幾何一號:黎曼非歐幾何
在<不假外求>這篇文章中,我們提到可將「球面幾何」視為內蘊幾何,只是從古希臘到十八世紀,一直沒有人抱持這種態度。
高斯在微分幾何中引進內蘊觀點,但並未利用這個觀點重新檢視球面幾何的定位。直到黎曼發表了上述那場演說,球面幾何才逐漸脫胎換骨,以嶄新的面貌出現在數學家面前。
不過,可別以為黎曼曾經拿球面幾何大做文章。事實上,他在演說中完全沒有提到「球面幾何」和「非歐幾何」這兩個名詞。因此下面兩個論點,其實是後人根據那篇講稿所做的延伸。
1.球面可視為獨立存在的二維空間,地位與平面不相上下。
2.球面上可定義廣義的直線,也就是所謂的「大圓」。
因此,想要讓「球面幾何」與「平面幾何」平起平坐,只要對歐氏(平面)幾何的前五個公理做些修訂即可。
歐氏公理一:任意兩點之間都能畫出一條直線。
這個公理在球面上也成立,不過這樣的「直線」有時並不唯一。例如任何經線(大圓的一半)皆以南北極為端點,如果你選取南北極這兩點,就無法在球面上定出唯一的直線。
歐氏公理二:一個線段的兩端可以延伸任意長度。
這個公理在球面上也成立,然而「延伸」的最後結果是形成一個大圓。如果讓大圓繼續延伸,就會一直自我重複。
歐氏公理三:使用任何圓心、任何半徑都能畫出一個圓。
由於球面範圍有限,球面幾何中的「半徑」必須有限制。
歐氏公理四:所有的直角彼此都相等。
這個公理在球面幾何中完全不必修改。
歐氏公理五(平行公理):在平面上有一條直線,以及線外一點,你剛好能畫出一條通過那個點且平行那條線的直線。
球面上任何兩個大圓都會相交,因此這個公理的後半部必須改為「你根本畫不出通過那點個且平行那條線的直線」。由此可知,球面幾何雖然本質上也是「非歐」,但並非高斯等人所發展的那種非歐幾何(亦稱雙曲幾何)。它的正式名稱是橢圓幾何(請參考<無用之用>),黎曼幾何則是它的代名詞。
●黎曼幾何二號:黎曼微分幾何
根據黎曼那場演說的講稿(嚴格說來是其中的微言大義),黎曼微分幾何具有兩大特點:(1)百分之百的內蘊幾何;(2)以N維流形為研究對象。
關於內蘊幾何,我們在<不假外求>這篇文章中已有詳細討論,至於第二個特點,因為牽涉到流形的定義,一定要從頭說起才行。
黎曼當初所定義的流形相當抽象,幾乎難以望文生義。幸好他舉了一個平易近人的例子──色彩是一種連續的流形──讓我們得以藉此體會他的想法。比方說,通常我們會用「色譜」或「色彩空間」作為色彩的具體模型,因此根據黎曼的定義,這些(一維、二維、三維)的幾何結構都是所謂的流形。
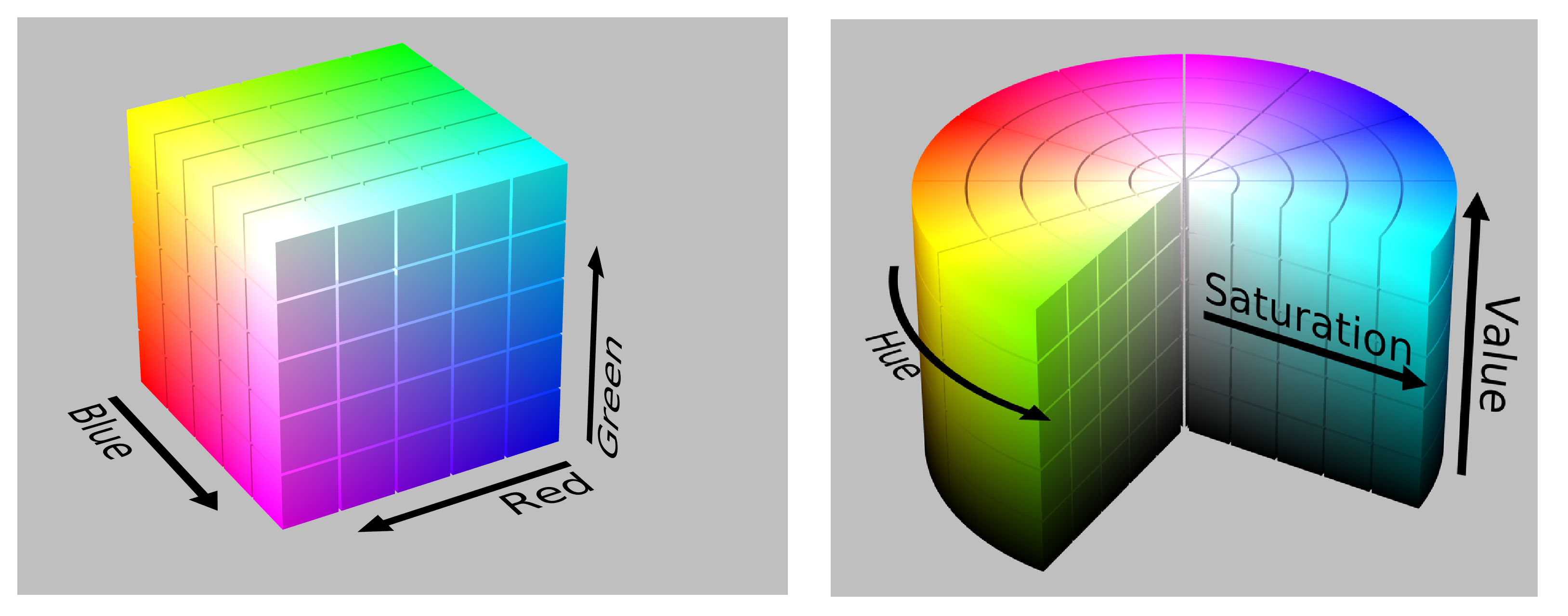
不過,經過上百年的淬鍊,如今數學家所說的流形已有明確的定義:凡是局部類似歐氏空間的幾何結構皆為流形。
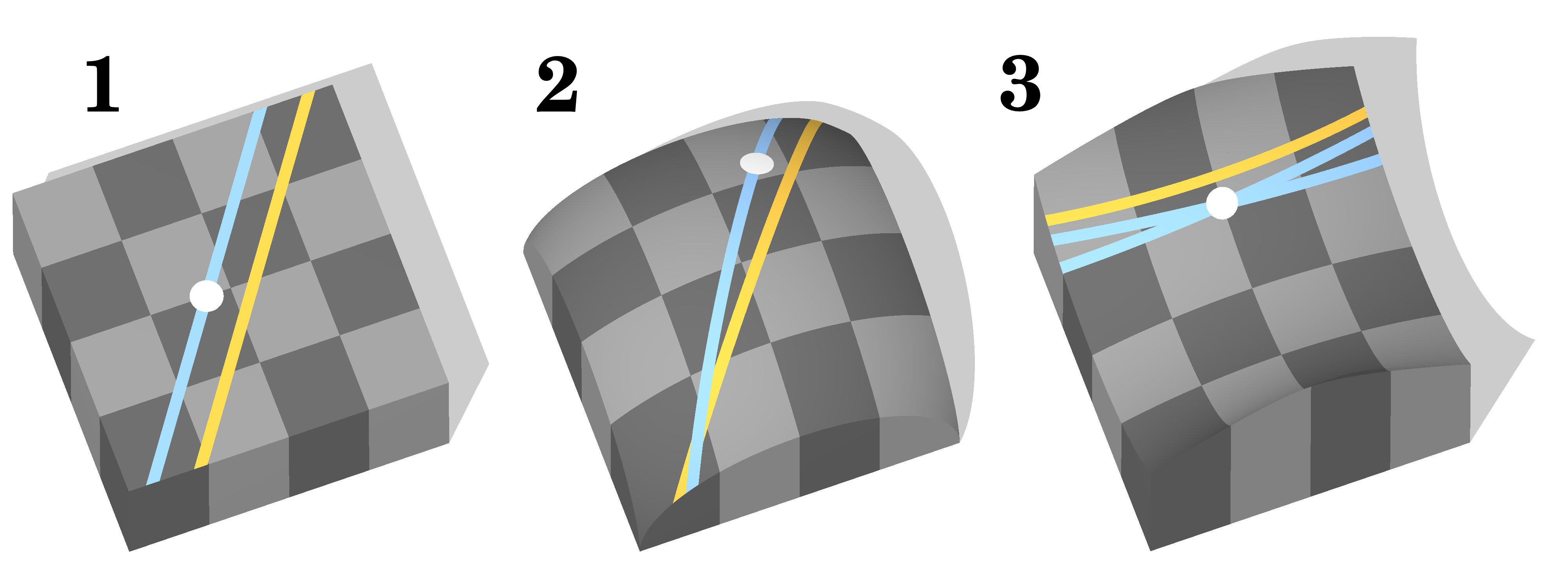
讓我們從一維說起,一維歐氏空間就是直線,所以拋物線顯然符合一維流形的定義──其中每個微小片段看起來都類似直線。
除了拋物線,還有哪些曲線是一維流形呢?比方說,圓或橢圓是否符合「局部類似直線」這個定義?只要想想阿基米德如何計算圓周率(請參考〈阿基米德與漢尼拔〉),你就會斬釘截鐵地給出肯定的答案。(圓的整體結構當然和直線大不相同,但那是另一個層次的問題,與流形的定義無關。)
不過,如果是自我相交的曲線,例如8字形,那可就不是流形了。因為正中央那點有四個分岔,並不符合「局部類似直線」這個定義。
那麼二維流形呢?二維歐氏空間就是平面,因此凡是符合「局部類似平面」的二維幾何形體都是二維流形。這意味著不論是馬鞍面或球面,甚至救生圈的表面,都符合二維流形的定義。
最簡單的反例則是在<無用之用>那篇文章中所討論的「疊羅漢圓錐」,原因和8字形類似,問題出在中央那個點上。
至於更高維的流形,雖然身為三維生物的人類難以想像,但由於歐氏空間很容易(藉由代數)從二、三維推廣到N維,例如五維空間的直角座標就是(a, b, c, d, e),因此流形的定義同樣不難推廣到任意維度。
更重要的是,由於黎曼微分幾何採用內蘊觀點,你在研究N維流形時完全不必引進更高的維度。正因為如此,我們這種三維生物能夠(根據黎曼發明的方法)測量出任何三維空間(例如整個宇宙)的曲率,正如同二維智慧生物能夠(根據高斯的絕妙定理)測量出二維流形的曲率。
附錄:「流形」考
為了便於討論,先列一個對照表:
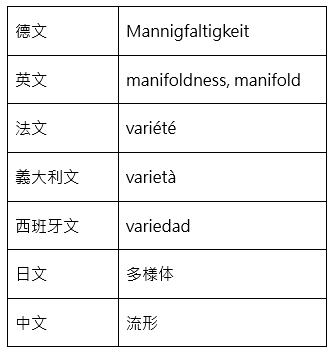
「流形」的源頭正是黎曼在1854年所做的那場演說,他將 Mannigfaltigkeit 這個德文賦予新意,當作數學名詞使用。它可以分解為 Mannig-faltig-keit 三部分,意思分別是「許多」、「皺褶」、「抽象結構」。
由此可知,如果直譯這個德文,最接近的中文名詞應該是「多層次結構」,但請注意這個「層次」不一定有具象的幾何含意。
1873年,黎曼的講稿由英國數學家克利福(William Clifford)譯成英文,其中 Mannig-faltig-keit 以一對一的方式譯成 mani-fold-ness, 後來則逐漸演變為 manifold 這個標準的英文數學名詞。
另一方面,法國數學家則採用類似意譯的方式,將黎曼發明的名詞翻譯成variété(等同於英文的variety)。其他幾個拉丁語系的譯名顯然和法文同出一源,甚至日文的「多様体」應該也是承襲這個傳統。
然而,中文的「流形」卻似乎是獨樹一幟,和上述兩個系統都沒什麼關係。不過為了避免驟下結論,我們最好還是考據一下「流形」到底是怎麼來的。比方說,我們很容易查到它的發明人是中國數學家江澤涵(1902-1994),出處可能是文天祥的《正氣歌》(天地有正氣,雜然賦流形),至於更深入的考據,就要靠自己努力了。
首先,由於「流形」和「幾何」同為中文的既有詞彙,因此無庸置疑,兩者都屬於賦予新意的譯名。其次,「流形」在中文裡原本是動詞,意指幻化成形,後來才逐漸變成名詞。
作為名詞的「流形」屬於「形容詞+名詞」這種結構,這時「流」最貼近的意思是「變幻不定、變化多端」,因而「流形」應該解釋為「多變的形體」或「多變的形態」,例如文天祥認為流形涵蓋了「河嶽」、「日星」甚至人體。
在這個解釋下,「流形」和「多様体」就很接近了。不過相信你會同意,前者顯然比後者更生動、更廣義。總而言之,下次再看到「流形」時,請別把「流」想成任何形式的流動,也別把「形」想得太具體,這樣才符合黎曼微分幾何的精神。
