量子霍爾效應（四）：迪拉克複合費米子

■這兩年物理學家提出了新的粒子電動對稱的理論解釋最低蘭道階（Landau Level）的物理，此新模型不再透過將磁通量附著到原粒子身上，而是藉由粒子漩渦對偶性，用更自然的方法去闡述一些實驗上觀測到的現象。

撰文｜蕭維翰

在前面幾篇文章中，我們介紹了量子霍爾效應的現象，並為分數與整數量子效應提供一些解釋。再者我們討論了 Jain 的複合費米子理論，指出實驗上觀測到的分數 1/3, 2/5, 3/7, …, 或2/3, 3/5,…, 等，都能被 Jain 序列所說明。在結尾處，我們指出 Jain 序列的極限是 1/2，在那個狀況下，複合費米子看不到磁場，並形成一個費米液體。針對這個問題， HLR 是一個知名的有效理論。

但這個理論還是有一點缺陷，而我們將說明並介紹一個解套的新提議。

回憶在單電子的圖像中，磁場中的二維電子系統基本上是蘭道問題，這些小於1的分數對應到的物理基本上都在第零階的蘭道階上，在理論的層次，由於不同蘭道階間的能量差約略正比於磁場強度[1]，考慮形式上的極限，如強磁場，可以讓我們丟掉其他蘭道階而專注在這裡。

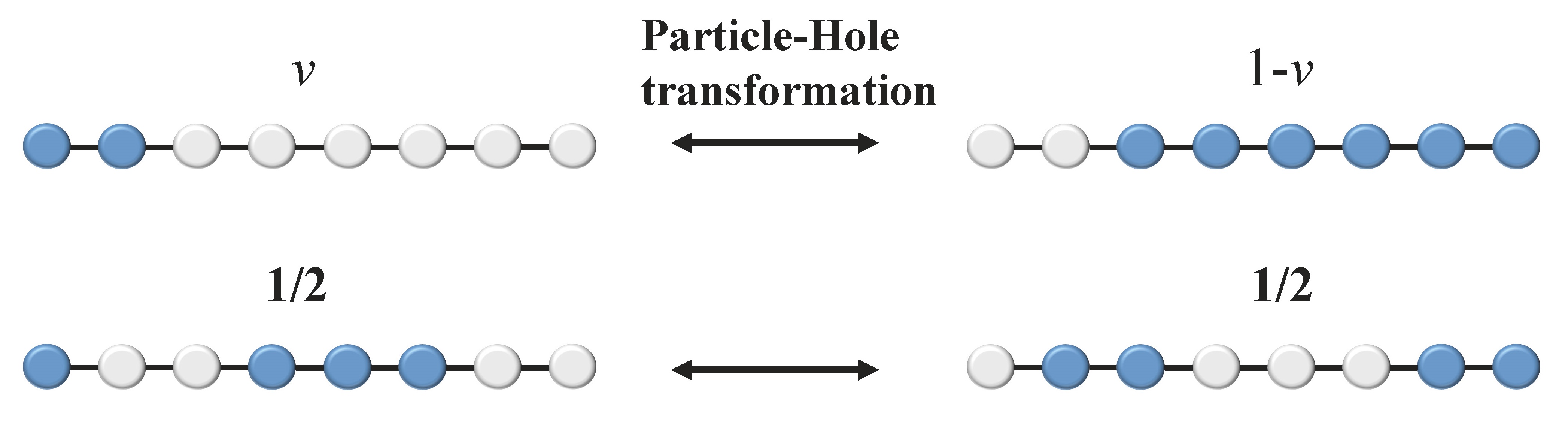
用卡通的方式來說明：現在我們感興趣的部分就只有一個蘭道階，裡面有一些房間，某些房間有住人（電子）。如果我們盯著這問題久一點，會發現如果將有住人的房子跟沒有住人的房子對調，這個問題似乎差不多。的確，在兩個 Jain 序列中，1/3 填滿經過這個操作後變成 2/3, 2/5 填滿變成 3/5，特別是 1/2 經過這個對調後，又回到 1/2，也就是說，一個描述 1/2 填滿狀態的物理理論，應該也要有對調電子跟空房後不變的特性。用比較炫的術語講，叫做粒子-電洞對稱。（particle-hole symmetry/symmetric）

可惜的是，無論是 Jain序列或者HLR 理論，至少在表面上，沒有顯著的粒子電洞對稱。譬如 n/(2n+1) 這個序列，它對應到 n 層填滿的複合費米子，而它的粒子電洞轉換 (n+1)/(2n+1) 卻對應到 n+1。要回答這個問題，可以有很多嘗試，比如：它只是看起來沒有，倘若我們小心地以維持粒子電洞對稱的方式做計算，這個對稱性是可以維持在物理量內的。也有人說，它原本有這個對稱性，只是在這個能量尺度，對稱性被自發地破壞了。幾十年來理論學家當然認真地朝這些方向在做修改，但結論並不是很明朗。[2]

另一種直接了當的回答方式則是：「那好吧，或許我們可以寫一個等效的，但具有顯然粒子電洞對稱性的新理論。」

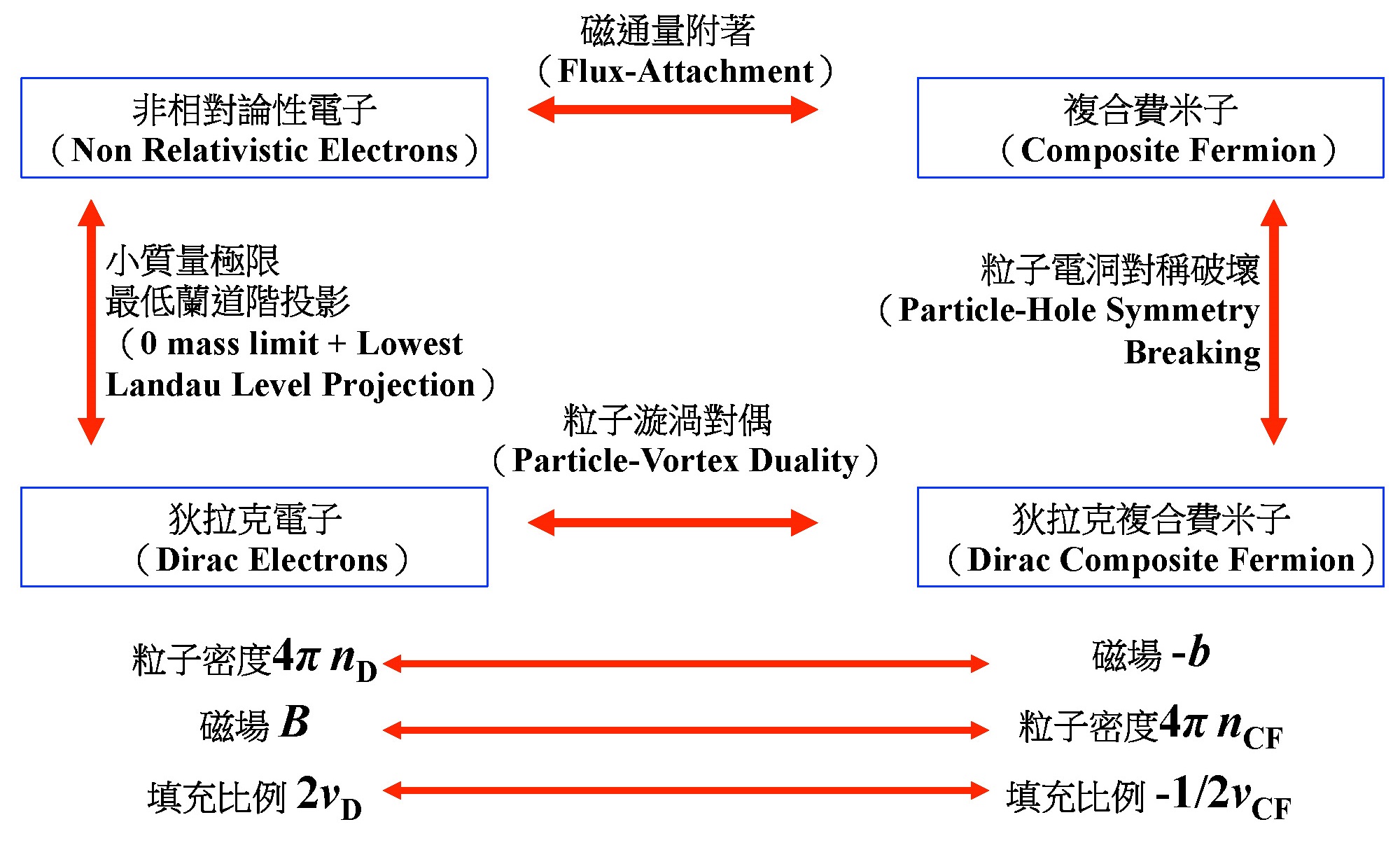
於是，在 2015 年芝加哥大學的 D. T. Son 提出一個新的等效理論。這個想法主要分為兩部分，首先他指出，除了考慮高磁場的極限，最低蘭道階也可以等效於考慮電子們的小質量極限，而在那個極限，非相對論性的費米子跟相對論性的狄拉克費米子是等效的。所以原本的非相對論性電子圖像，就變成了狄拉克電子。那麼原本的複合費米子呢？Son 了解到，這個新的狄拉克複合費米子，不能跟原來的 HLR 一樣，直接寫成一個電子加上兩個磁通量。在粒子電洞轉換之下，一個電子變成一個電洞，這個新的複合費米子不能傻傻著照做，不然就解決不了在1/2 填滿態粒子電洞對稱性的問題。

結論是，新的狄拉克複合費米子，約略而言是「狄拉克電子的漩渦」，也就是在第二篇「物理學中的對偶性」所提到的費米子版本粒子-漩渦對稱。

作為一個有效理論，Son 的提議要能解決現有現象學上得知的事實，譬如在 1/2 填滿時，複合費米子形成費米液體，或者 Jain 序列。令人驚訝的是，至少就這兩個現象而言，狄拉克複合費米子給出的解釋都是很清晰簡單的。

首先因為狄拉克的光譜中，有無限深的負能量態，或說狄拉克海，填滿的狄拉克海會提供背景的電荷密度，導致狄拉克電子的填充比例ν_D與原霍爾問題的填充比例ν_NR差了 1/2，ν_D=ν_NR-1/2。原來霍爾問題中的ν_NR= 1/2 態因此對應到了狄拉克電子的電中性態ν_D=0，粒子電洞對稱性是顯然的。再者，漩渦粒子對偶性將狄拉克電子的粒子密度對應到狄拉克複合費米子的背景磁場（反之亦然），所以在磁場中的電中性狄拉克電子對應到具有有限密度的但無磁場的複合費米子，因此是一個費米液體。

如果我們調整系統中的人口壓讓狄拉克電子具有密度，則對應的是開啟狄拉克複合費米子系統內的磁場，從而在複合費米子這端也形成蘭道階，並且可以定義填充比例ν_CF。Son 透過漩渦粒子對偶演算得出，ν_Dν_CF = -1/4，當ν_CF= n+1/2時， ν_D =(n/(2n+1))-1/2，而當ν_CF= -(n+1/2)，對應到ν_D =((n+1)/(2n+1))-1/2。這個有效理論也以維持粒子電洞對稱的方式，解釋了兩個 Jain 序列，ν_NR =ν_D +1/2= n/(2n+1)  與 (n+1)/(2n+1)。

兩年來這個新提議引起了一些討論，目前有些量子霍爾效應的專家也還抱持著質疑的態度。[3]也有學者們在進行計算，試圖尋找這個提議與 HLR 理論在預測能力上的差異。但至少 Son 本人的部分看法是，原本的複合費米子圖樣雖然是很有創意也很漂亮的點子，然而在現象學上，他認為漩渦粒子對偶性提供了分數量子霍爾效應一個比較自然的說法。

 

註解：

[1] 正比於古典電子在磁場內轉圈的頻率，這個頻率可以在高中物理課本內找：qB/m。

[2] 關於對稱性的自發破壞，可參見陳奕廷＜自發對稱性破壞和多體效應＞。

[3] 譬如 HLR 理論的開創者們便不太會願意全盤接受。

 

參考資料：

1. D. T. Son, Is the Composite Fermion a Dirac Particle?, Phys. Rev. X 5, 031027 (2015).
2. D. T. Son, The Dirac Composite Fermion of the Fractional Quantum Hall Effect, Prog. Theor. Exp. Phys. 2016, 12C103.

--
作者：蕭維翰，臺大物理系畢業後逃到芝加哥，吹風吹雪之餘，做研究讀博士班。可惜離開臺灣後無海可看，只能在密西根湖旁揀一方堤岸，偽裝成看海的人。科教中心特約寫手，從事科普文章寫作。