【物理世界】量子霍爾效應(三):複合費米子
■在 Laughlin 波函數後,J. Jain 提出了複合費米子的概念,將整數量子霍爾效應與分數量子霍爾效應結合在一個框架下,並成為研究量子霍爾效應的一個典範。

撰文|蕭維翰
儘管 Laughlin 波函數從定量的角度提供了當時人們了解某些分數霍爾態的出發點,它並不稱得上是一個完整的「故事」。另一方面,它的成功也多侷限於1/3. 1/5 等分數,而不涵蓋其他如2/5, 3/7 等也在實驗中被發現的狀態。
Jain 在1989 年提出所謂複合費米子(composite fermion)的概念 [參1],希望以它來提供整數量子霍爾效應與分數量子霍爾效應一個統一的圖像。顧名思義,相對於電子這種「基本粒子」,複合費米子可以被理解成是電子綁上其他元素,在更早的核子物理中,一個核子也可視為複合粒子(composite particle)(儘管不一定是費米子)那時其他元素可能是質子、或中子,而在量子霍爾效應中,這個元素抽象的多:我們要將電子和磁通量[1]綁在一起!
這個主意背後的動機或者可以這麼理解:在前面兩篇文章中我們都談到了住公寓這個比喻,要把公寓跟系統中牽涉的物理量結合,磁場這個局域的量並不合適,相對而言,總磁通量與整個系統大小(即公寓房間數目)成正比,是一個比較好對應的量。平均來說我們可以想像每個房間都可以有一個朝上的小箭頭來代表,這個箭頭帶有一個磁通量的單元[2],經過計算它的大小是 hc/e,其中 h, c, e 分別是普朗克常數、光速與電子電量。
Jain 所謂的複合費米子就是將一個電子綁上 2, 4, 6, …等偶數個磁通量箭頭形成的新費米子[3]。
這樣做會獲得什麼結果呢?首先我們考慮1/3填滿的分數霍爾態,從定義上知道,這個態中若有N個電子,就會有3N個房間(小箭頭),如果將每個電子都綁上2個磁通量小箭頭形成一個複合費米子(簡稱CF2),整個系統就會剩下N個複合費米子與N個磁通量小箭頭,這不是別的,就是整數量子霍爾效應中填滿第一層蘭道階的狀態!(見圖一)
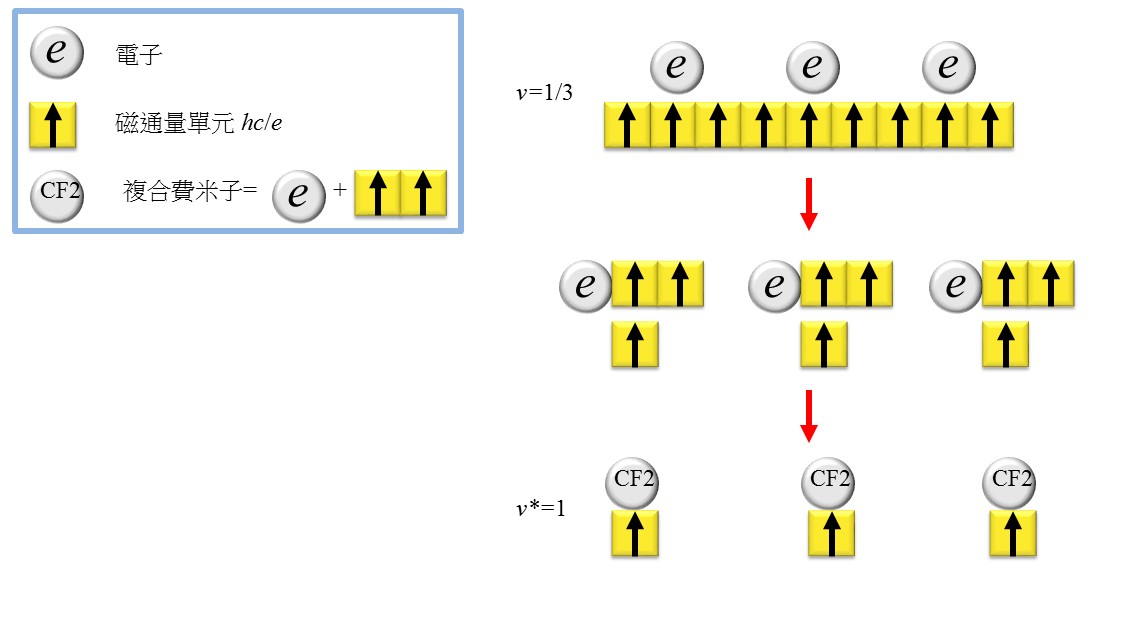
更進一步來說,我們用CF2組成一個填滿n層蘭道階的整數量子霍爾態,即系統中會有N個朝上箭頭以及nN個CF2。接著將每個CF2拆解成一個電子跟2個小箭頭,則整個系統變成有nN個電子與(2n+1)N個小箭頭,對應到的就是n/(2n+1)=1/3, 2/5, 3/7,…的分數霍爾效應態。同樣的遊戲也可以這麼玩:用CF2組成一個填滿n+1層蘭道階的整數量子霍爾態,但將磁場的方向反過來,系統中會有N個「朝下小箭頭」以及(n+1)N個CF2,將複合費米子拆解回電子和朝上小箭頭後,這個系統會對應到(n+1)/(2n+1)=1, 2/3, 3/5, 4/7,…等態。 (見圖二)
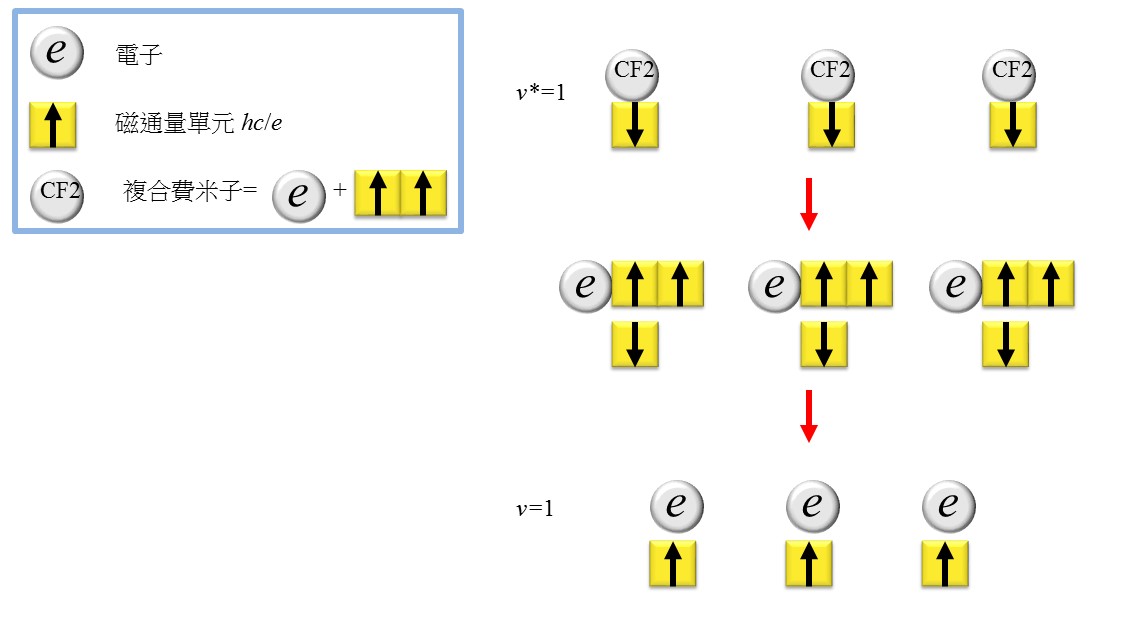
這兩個序列稱為Jain 序列 ,透過複合費米子的圖像,Jain不僅將整數與分數量子霍爾效應納進同一個框架,指出「電子的分數霍爾效應即複合費米子的整數霍爾效應。」也比單純的 Laughlin 波函數解釋了更多實驗上發現的分數。
然而,這個理論依舊不是很完備。其中一個很顯然的缺陷是,在霍爾效應的問題中,原則上在磁場夠大的情況下,所有的物理應該只跟最低層的蘭道階有關,但將問題變成複合費米子的整數霍爾效應時,不可避免地會使用到高層蘭道階,因而在進行計算時我們必須手動地去將高層蘭道階成份去除。也因此有其他學者嘗試從其他角度,去建構有效理論或波函數 [參2, 3]。
另外一個物理學家感興趣的點是,Jain 序列在 n 在無窮大的極限是 1/2,如果套用上面貼附磁通量的論述,系統中有 2N 個朝上小箭頭與 N 個電子,在轉換成 CF2 後,會變成 N個CF2但「沒有磁場」。B. Halperin、P. Lee 和 N. Read 首先在1993年提出現今人稱的 HLR 理論來描述這個 1/2 填滿的態 [參4],但直至 20 年後,為了釐清問題中不可或缺的對稱性,一個新的發想再一次地這個 1/2 填滿的態發出衝擊。
參考資料:
1. K. Jain, Phys. Rev. Lett. 63, 199 (1989).
2. N. Ginocchio, and W. C. Haxton, Phys. Rev. Lett. 77, 1568 (1996).
3. H. Hansson, M. Hermanns, S. H. Simon, and S. F. Viefers, arXiv: 1601.01697 (2016).
4. I. Halperin, P. A. Lee and N. Read, Phys. Rev. B 47,7312 (1993) .
註釋:
[1] 國中理化我們會學到磁通量的變化會產生電動勢(電壓差),這是發電機的基本原理,跟這邊講的磁通量是一樣的東西,約略而言即磁場乘上面積。
[2] 也就是磁場乘上面積除以每個蘭道階的房間數目。
[3] 非得是偶數個磁通量單元是有重要理由的,但要講述這個大概又得另外寫一篇文章,在量子物理中有一個所謂Aharonov-Bohm效應,指出在準二維系統中,一個粒子的波函數繞過一個磁通量時會乘上一個大小為1的複數。簡單地說,費米子要黏上偶數個磁通量單元hc/e,才能還是一個費米子。
--
作者:蕭維翰,臺大物理系畢業後逃到芝加哥,吹風吹雪之餘,做研究讀博士班。可惜離開臺灣後無海可看,只能在密西根湖旁揀一方堤岸,偽裝成看海的人。科教中心特約寫手,從事科普文章寫作。
