摺紙：摺痕中的數學

■CASE讀報和「一張紙變變變」研究計畫合作，推出為期一年的摺紙專欄。透過摺紙藝術介紹生物多樣性，或者導入一些數學概念，讓科學變得生動有趣！-----歡迎加入【一張紙變變變】粉絲團！

撰文｜西新英格蘭大學數學系副教授　湯瑪斯·赫爾
翻譯｜涂瑋瑛

摺紙藝術為發源於日本古代的技藝。摺紙藝術家可以將一張未經裁切的方形紙摺成一隻鳥、一隻青蛙、一艘船或一隻日本獨角仙。事實上，摺紙藝術的複雜是超乎想像的。

摺紙藝術在過去30年內經歷了「文藝復興」，創造出更複雜的新設計。隨著摺紙複雜度提高，科學家、數學家及摺紙藝術家也發現越來越多蘊含於摺紙設計中的數學規則，而這種現象並非巧合。

如果你有一個摺紙作品，例如一隻紙鶴，當你仔細拆開紙鶴後會發現，紙上的摺紋樣式就像作品的藍圖。摺紋樣式包含將紙張摺成紙鶴的秘訣──亦即數學。理論上，我們能使用摺紋樣式來決定摺紙方法及作品樣貌──前提是我們能了解摺紙的所有數學規則。

 

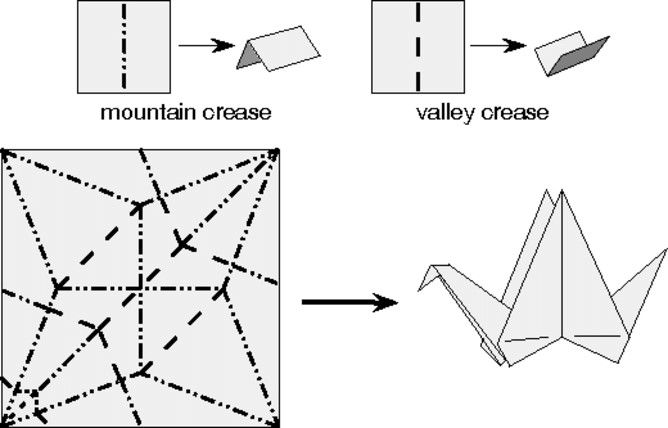
●解讀摺痕

數學的核心是了解宇宙的規則及規律，不論是數字、股市或是自然中的規律，都屬於數學的範疇。至於摺紙中的數學，我們需要研究摺紋樣式的幾何學，包括線條在哪裡交會？它們形成的角度為何？摺痕摺疊的方向為何──亦即摺痕是山摺線或谷摺線？

傳統摺紙模型大多能摺疊成扁平形狀，換句話說，傳統摺紙模型能壓在書裡卻不會起皺。我們發現這種平面摺紙模型的摺紋樣式有些非常特別的屬性。其中一項特性稱為前川定理（Maekawa’s Theorem）：在一平面摺紙作品的摺紋樣式中，山摺與谷摺的數量差異在每個摺痕交會點上永遠為二。譬如在一摺痕交會點上可能同時出現5個山摺及3個谷摺，但絕對不會有6個山摺及2個谷摺。

 

●從藝術到應用

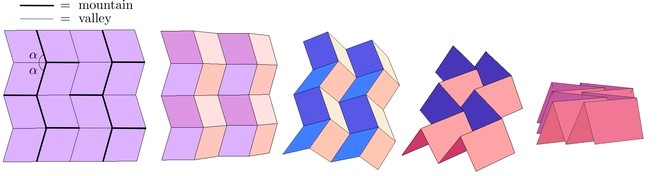
在1970年代，日本天文物理學家三浦公亮發明了「三浦摺疊（Miura map fold/Miura-ori）」。這是一個摺紙鑲嵌的實例，亦即同一形狀在整個平面上無間斷重複。在三浦摺疊中，因為摺紋樣式為平鋪排列的平行四邊形，所以摺痕線條也具有平面摺紙作品的特性。由於三浦博士選擇使用特定數量的山摺線與谷摺線組成摺紋樣式，因此三浦摺疊非常容易展開與閉合。

因為這種摺紋樣式能輕鬆展開與閉合地圖，所以摺疊地圖時使用這種摺紋樣式是極好的選擇，但是三浦博士將摺疊設計進一步運用在展開外太空的大型太陽能板。假設把每個平行四邊形都想像成一個太陽能電池，而所有電池都以絞鍊連結，那麼這一系列電池能摺疊成一個小型套裝，在火箭發射前放在人造衛星上。一旦進入太空，這個小型套裝能以一支簡單擴展桿打開，而不需要人工手動開啟。

三浦摺疊已經鼓舞許多研究人員探索其特質、運作原理及使用方式。舉例來說，來自馬薩諸塞大學阿默斯特分校（University of Massachusetts-Amherst）與康乃爾大學（Cornell University）的研究人員組成一個團隊，與我一起研究三浦摺疊在機械設備的應用：壓縮摺疊設備時需要多少力量？而放鬆設備時，其回彈的力量又是多少？我們在《科學（Science）》期刊上報告研究成果，發現如果在三浦摺疊上添加一些缺陷，譬如將某些摺痕交會點戳往反方向（譯註：例如將三條山摺的交會點（凸點）變成三條谷摺的交會點（凹點），反之亦可），就能改變三浦摺疊的運作方式。下圖顯示其中一種實例。

我們團隊也正在研究自行摺疊（self-folding），並製造了一些能自行摺疊的材料。除了我們團隊，也有其他研究團隊對這個主題感興趣。在康特國家聚合物研究中心（Conte National Center for Polymer Research）的萊恩·海沃德（Ryan Hayward）研究團隊已經研發出一種方法，使微型凝膠片在受熱後能沿著摺痕線條膨脹。這種方法可製作出一隻微型鶴鳥：

這隻鶴鳥可能是有史以來人類所摺出的最小鶴鳥！這種自行摺疊聚合物凝膠能製作出非常複雜的設計，例如這種立體八面體－四面體桁架鑲嵌結構：

未來這種微小的自行摺疊凝膠物體可能會運用於生物工程領域。想像一下，將某種高毒性的抗癌藥物封裝在一顆自行摺疊的摺紙小球中，這顆小球設定為只在接觸腫瘤時才會展開。如此一來，藥物就能精準投入腫瘤，卻不會毒害病患身體其餘部位。

假使我們不了解摺紙背後的數學規則，上述這些摺紙應用就不會實現。這告訴我們，數學與摺紙的應用非常廣泛，甚至能出現在我們原本意想不到之處。

--
作者簡介：湯瑪斯·赫爾是摺紙數學的權威，並在全世界巡迴演講來介紹這個主題。他的研究使用圖論、組合學、幾何學及其他數學領域，並應用於工程學、材料科學、藝術及教育。他是數學俱樂部的指導教師，喜歡讓學生參與他的研究，他也定期在教師數學進修計畫教導學員。另外他也喜歡參加飛盤爭奪賽、閱讀恐怖靈異故事。現任西新英格蘭大學數學系副教授。

原文出處：Origami: mathematics in creasing