【數學概念】這片土地的樣貌--淺談拓撲學

撰文|吳如峰
在上一篇文章中,我們在最後留下了一個問題:這個世界是否存在真的連續的東西呢?今天就讓我們來回答這個問題吧!但在回答這個問題之前,我們要先談一談我們這塊土地的樣貌。
啊?什麼?這跟土地的樣貌也有關係?
這麼說好了,這是語言上的關係。在古希臘,「土地樣貌的學問」就是由兩個字所拼起來的:”τόπος”代表「土地(place)」的意思、”λόγος”代表「學問(study)」的意思,因此” τοπολογία”就是「研究土地的學問」的意思,這個字翻譯成中文就成了現在大家耳中的「拓撲(topology)」。在十九世紀中期,數學家們把這個概念引進到數學裡面,當時主要的問題就是為了研究數學分析,講得簡單一點,就是在研究一些跟連續函數有關的問題。
那「拓撲」到底是什麼呢?數學家給了下面這個容易令人頭昏的定義:
對於任意一個集合X(全空間),如果存在一個X的子集合的集合T使得T滿足下列三個條件:
- X及空集合都落在T裡面
- T裡面的集合的任意聯集也落在T裡面
- T裡面的集合的有限交集也落在T裡面
那麼,我們便稱T為X的拓撲
要具體地說明這個定義,我們必須借助一些例子來幫助我們了解。這個例子必須要請讀者們回想當初在學習微積分時時常使用的「開區間(open interval)」:在實數線上我們定義一個開區間(a,b)為一個搜集所有大於a且小於b的所有實數的集合。
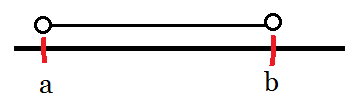
並且,我們也把整個實數線及空集合定為開區間。那麼當我們考慮T={所有開區間},我們可以發現:整個實數線及空集合都在T裡面、開區間們得任意聯集也是開區間、開區間的有限交集也是開區間。於是T就滿足了我們上面給的拓撲的定義,也就是說,T就是實數線的拓撲。
從這個例子來說,我們可以發現:原來我們上面給得那個拓撲的定義只是在定義一個集合裡面的開區間是什麼而已。講到這裡,你或許會問說:那開區間又代表著什麼?我們幹嘛定義一個集合得開區間?
其實簡單來說,開區間就是告訴你哪些東西很靠近,也就是說哪些東西式鄰居:當兩個數很靠近時,代表他們是鄰居,也就是說會存在一個對兩個數都鄰近的區域(neighborhood)把兩個數都包含在裡面,而越靠近的數就可以找到越小的開區間同時包含這兩個數。譬如說大安區與中正區很靠近,所以可以用台北市做為一個鄰近的區域來將兩個直轄市都包含在裡面,在這個拓撲裡頭,你所使用的「開區間」就是「全臺灣的縣市」、而全空間是「臺灣」;又或者說你可以把全世界視為一個全空間、那麼臺灣的各個縣市就會彼此靠得很近,與大陸的就會距離遙遠。
回到我們的定義上,由於我們的定義是可以定義在任何一個集合上而不一定要定在實數線上,於是我們把T裡面的這些集合稱為「開集(open set)」,或者就直接稱做open neighborhood。
而我們剛剛在不同的全空間上看到了不一樣的拓撲,那麼是不是同一個空間上可以定出不一樣的拓撲呢?答案是:是的。最簡單的兩個例子就是:對於任一一個集合X,我可以只蒐集X與空集合到T裡面,那麼T會滿足我們的條件(數學家們稱這樣的拓撲為密著拓撲(tirvial topology));另一個則是,我把X裡所有的集合都蒐集到T裡面,那麼T也會滿足我們給的拓撲的條件(數學家們稱這樣的拓撲為離散拓撲(discrete topology))。
說到這裡,或許你會不禁納悶:這到底與連續不連續有什麼關係呢?在上一篇文章中,我們已經有提到:如果有一個存在兩個拓樸空間之間的映射,這個映射在某一點連續若且為若任意包含這個點函數值的開集的逆向是包含這個點的某個開集。所以,說穿了,一個連續映射只是在說明兩個空間中的拓撲有多麼雷同。
於是,當我們考慮我們現實空間中的拓撲為密著拓撲時,那麼所有在原本的拓撲之下不連續的事物,突然間就變得非常的連續了!
