【神經科學】從神經科學角度看數學之美

■羅素曾說：「如果我們好好觀察，會發現數學除了蘊含真理，更蘊含了無與倫比的美。」

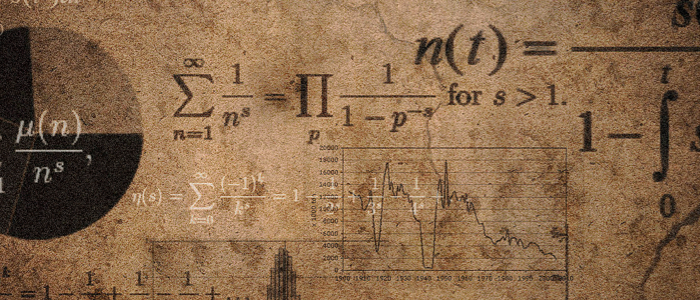作者｜Scott Barry Kaufman
編譯｜柯宗佑

最新的神經科學研究指出，視覺、音樂、道德美感是由某部分的「情緒腦區」，也就是額葉中區皮質(medial orbitofrontal cortex, mOFC)所掌控的。

那數學呢？柏拉圖認為，最頂級的美，就是數學的美了，因為數學全然是人類才智的結晶，更蘊含了宇宙真理。藝術評論家克里夫．貝爾(Clive Bell)也抱持類似看法：

「藝術將我們帶離世俗，提升到美的至高境界。頓時，我們會忘卻一切利益考量，各種期盼與記憶不復存在，全然超脫塵世了。全心全意投入研究的數學家，他們的心靈狀態也差不多如此。他們心頭可能會浮出某些猜想，這些猜想與俗世毫無瓜葛，會以非人甚至超越人類的姿態，自抽象的科學世界脫胎而生。有時候我在想，欣賞藝術的人，會不會和欣賞數學解題方法的人一拍即合。」

一項新研究認為，貝爾的說法可能是對的。研究人員賽米爾．澤奇(Semir Zeki)與同事找了十六位具碩士及博士學歷的數學家，以及十二位非數學家作為受試者，進行實驗。受試者先進入核磁共振儀，再閱讀一系列數學方程式，接著針對方程式的美感程度，以及個人是否了解方程式內容給分數。受試者離開共振儀之後，還要填寫問卷，回答自己對方程式內容的了解程度，與閱讀方程式時的情緒反應。

底下這個方程式是眾人公認最美的(尤拉恆等式)：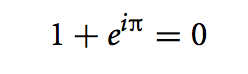

自選美比賽脫穎而出的，還有畢達哥拉斯三角恆等式、複分析中導自尤拉公式的指數及三角函數恆等式、柯西-黎曼方程式等。反之，以下這個由斯理伐沙．拉曼努札(Srinivasa Ramanujan)導出的1/π無窮級數方程式，則是公認最醜的：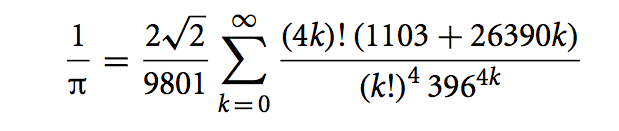

其他不討喜的方程式，還有黎曼函數方程式、可用兩種不同的兩立方數和表示的最小數字、以及態射的像與下一個態射核心相同的正合數列。

研究人員從大腦掃描影像中發現，處理數學之美的腦區，和處理視覺、聽覺、道德美感的腦區是同一區塊，也就是額葉中區皮質的A1區。此外，當受試者感受越深刻，該腦區的活動就越劇烈。有趣的是，理解和感受到美完全是兩回事。受試者中的數學門外漢，就算對方程式一竅不通，也發現某些方程式就是比較美。額葉中區皮質A1區之所以會產生活動，其實與理解方程式無關，而是與感受到美有關。

不過要注意，不要看了這些研究結果，就以為領略數學之美全都依賴額葉中區皮質。事實上，其他在觀畫、聆樂不會被活化的腦區，在閱讀方程式時反而會被活化。但總而言之，領略不同美的共通結果，就是額葉中區皮質A1區都被活化了。此外，這項發現不必然表示該腦區專門負責美感經驗。額葉中區皮質A1區的功能很多，包括處理情緒、學習、愉悅感、酬賞等。

再者，該腦區的神經元也並不見得是讓人感受到數學之美的動力來源。這些研究結果所指出的，僅僅是閱讀數學方程式時，腦區活化與美感經驗彼此是有相關的。

不過話說回來，看了這些研究結果，我們反而產生了新疑問：如果數學之美不見得和理解方程式有關，那數學之美從何而來？研究人員認為，「美是種抽象事物，是超然於文化或學習經驗之上的。」他們猜測，數學門外漢鑑賞數學之美時，並不是奠基於理解內容之上，而是根據方程式的外觀、對不對稱等結構特徵。

然而，研究人員進一步指出，美感或許是通往自然真理的道路。的確，柏拉圖曾經強調數學式很美，因為我們能從中窺見宇宙的基本結構。理論物理學家保羅．狄拉克(Paul Dirac)也同樣表示：

「自然學科為何得使用數學推理，我們無法用邏輯解釋，不過實作時，數學對自然科學確實有幫助，成效頗佳。真要解釋，大概是因為數學蘊含了某些自然規律。這些規律不為一般人留意，卻是世界運行的重要推手。相對論與簡約原則背道而馳，卻廣受物理學家支持，這正是因為其中蘊含了數學之美。在數學中，這項特性無法定義，不像藝術領域能定義何謂美，但儘管如此，研究數學的人領略起來仍毫不費力。相對論讓我們看見數學之美以及自然規律，深刻程度前所未見。我們現在知道，我們必須捨棄簡約原則，轉而投入數學之美的懷抱。使用數學符號描述自然規律的研究者，應該大力追求數學之美，雖然可以同時追求簡約，但美必須先於簡約。簡約和美的要件大體相同，但要件相互牴觸時，美的優先次序依舊在簡約之前。」

人們常爭論審美經驗可否量化，或是討論美感經驗與愉悅感、酬賞的關聯究竟多深。根據這些研究結果，我們多少能解釋何謂審美了。箇中道理，值得我們好好思考！

延伸閱讀：
《BBC知識》人腦的美麗境界
【星空特輯】克卜勒與和諧之美
【我的數學夢】告解數學
--
研究出處：The Neuroscience of Mathematical Beauty
譯者：柯宗佑 科教中心特約寫手，從事科普文章編譯。
責任編輯：Kerina Huang