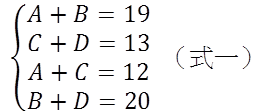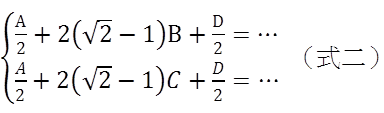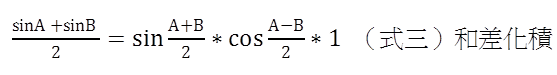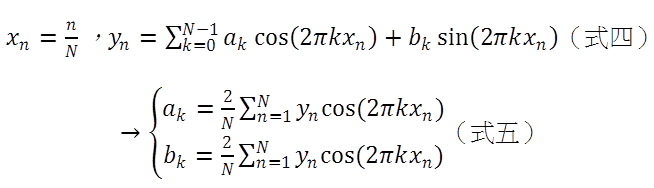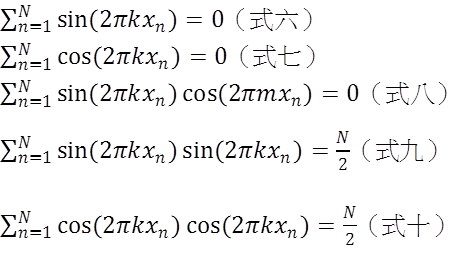【探索十】醫學影像中的數學

第八講‧特稿

■「你今天好sec！」成功大學舒宇宸教授，在「聽數學與生命對話」的最後一講「醫學影像中的數學」，成功地找回「數學」在臺灣的制式教育下，佚失的趣味性。「生活中有數學，只是數學大多被隱藏起來，你要把它找出來。」老師以時尚且年輕的語彙，讓同學們學數學不再「sec」（囧）。

撰文│郭冠廷

數學與生命是有交集的！

「如果x不屬於a，那麼a是空集合。」這是邏輯課程上會出現的句子。而事實上，它也是我們日常生活中的語句[1]。所以宇宸老師說：「生活中有數學，但是要發揮自己的想像力。」而數學與我們的生活息息相關，不僅僅具有成為「火星文」語彙的潛能，亦藏匿在我們的每一通電話當中。在知名動畫《名偵探柯南：戰慄的樂譜》中，就有一齣誇張之餘，又不失真實的一幕，描述主人翁柯南與音樂家用兩個不同頻率的「歌聲」來撥通「電話」的特技表演。宇宸老師在演講中讓大家聽把兩個正弦函數加在一起的一場魔術表演，說明了柯南劇中的神奇之處。我們從國中開始接觸三角函數，認識sin、cos、tan，甚至每天向師長哀號：「學數學有什麼用？」其實我們現行電話所採取的「電話撥號音（DTMF，Dual Tone Multiple Frequency）」，就是由兩組頻率的sin波所組合而成[2]。套句時下流行的話：「如果這不是數學，那什麼才是數學？」

環環相扣的數學知識

CT影像透過Randon Transform來轉換資訊，而超音波影像是根基於Hibert Transform。而不論是Randon Transform或Hibert Transform，都與傅立葉轉換有著密切關係。而這些知識，可以追溯到國高中所學的：聯立方程式、基底、三角函數、和差化積、正餘弦疊合等。

 

解聯立方程式

醫療上常用的「CT影像（CT，computed tomography），與「數學」關係密切是我們已經瞭解的事情。但是這些數學知識在高中時我們就已經通通學過，這卻是我們前所未聞的驚人消息。宇宸老師用「高中數學」中的「聯立方程式」來解釋CT影像。

X光，是一種波長在0.01nm到10nm的電磁輻射。利用高電壓的真空管，撞擊陽極的金屬而得。而當人體接受X光時，不同的身體組織會吸收不同程度的X光。因著X光被吸收程度的差異，在底片上就會呈現出身體內部的構造。而CT影像，則是從不同的方向拍攝病患的X光片，利用諸多的X光資料來重建病患身體內部的結構。

宇宸老師為了讓我們瞭解CT影像的原理，準備四張撲克牌A、B、C、D。這四張牌分別代表我們身體內部的某種組織，但是我們不清楚這四個組織對X光的吸收程度為何？我們只知道，當X光以橫向照射病患時，會得到兩組吸收的數值「19」、「13」；而當X光以縱向照向患者時，會得到另外兩組吸收的數值「12」、「20」。我們就由這二組數字，去回推A、B、C、D四個組織，對X光的吸收程度。

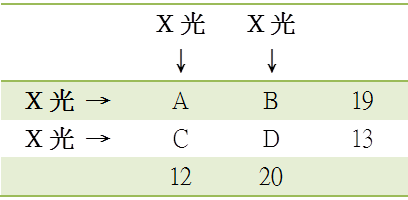
因此，要做出CT影像，就是要成功解出這些未知數。而從聯立方程式：

 

我們會發現若只有兩個方向的資訊（二切）要解出四個未知數，是不會得到唯一解的。因此，我們嘗試加上第三個方向，從45度角取得兩條式子（式二）。

以（式一）和（式二）為基礎，我們就可以得出A、B、C、D的吸收程度圖，也就是「三切」的CT影像。

 

超音波

超音波也是醫療的寵兒，而本於「聲波」的超音波，更是與數學緊密相連。音波是疏密波，我們可以將聲波以波動的圖形表示。而數學中的週期函數，更可以用來拆解聲波的圖形，而將聲波拆成數組的數學方程式。而和差化積（式三）、離散的傅立葉轉換（Discrete Fourier transform）是我們手中的重要工具。

離散的傅立葉變換是一種線性的變換。而過程就是高中所談的「Σ（Sigma）」。因此，宇宸老師就從離散的傅立葉變換來解釋，讓我們驚訝於知識累積的過程。高中所學的知識，確確實實能應用在我們的生活當中。我們把機器偵測到的超音波波動，大膽假設其波型是cos和sin的組合，按照某個係數把它加起來（式四）。

 

 

 

而在證明這組猜測的過程當中，我們會需要用到幾個重要的等式：

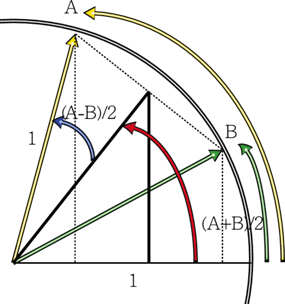
透過離散的傅立葉變換，我們獲得（式五）中的a_k與_bk，如此就成功將波分解正餘弦函數的組合。再透過Hilbert轉換可以求得這個波的波包。而超音波，就是利用探頭發出超音波。藉由超音波打到物質後反彈的訊號，再由接收器收集訊號，並透過機器（amplifier）將微弱的訊號放大。然後透過運算取得聲波波包的振幅，並將振幅取「log」，按照探頭的次序排列成一個二維影像，這就是我們在超音波機器螢幕上所看到的B-mode影像。

數學家從事醫學研究

語言的轉換非常的重要。化學本科出生的竹亭老師這麼說：「化學是探究物質，和相關的科學。從二十世紀中期以後，我們很清楚意識的知道。除了物質能量以外，資訊。物質和人之間的資訊，是很有趣很有意思的。」人的腦，可以瞭解這當中的許多資訊是什麼意思，一旦瞭解就可以去解讀。這種解讀很多是靠著數學。「這個世界，去理解時。有物質，有人，有資訊。」

當宇宸老師剛開始接觸醫學研究的時候，也碰到許多的困擾。萬生老師補充：「概念的轉換（轉譯）的過程非常的重要。我們怕研究的東西（在轉換過程當中）消失。」宇宸老師說明，他一開始也不曉得什麼是肝纖維化，合作的醫師就得要向他們慢慢解釋。「我們要去瞭解他們（醫生）的行話。」當老師理解，肝上頭會硬化、產生不平滑的顆粒，就必須要將這個醫學上的現象，轉換成數學的語言（homogeneous）。

 

溯源臺灣

宇宸老師也熱情地分享一部臺南的觀光影片給觀眾欣賞，而這充滿臺灣味的在地介紹，也正巧銜接起我們科教中心對認識臺灣的關心。我們將在下一期的探索講座，規劃一系列溯源臺灣的講座。明年春天，第十一期的探索講座，將由中研院的史語所的劉益昌劉博士策畫。來談臺灣自然、地形、生態、地質、人文的溯源。是科教中心對於跨領域學習的全新嘗試。這一期講座的尾聲，陳竹亭主任勉勵大家：「Life is for learning.」歡迎您的蒞臨。

---

 

---
 本文整理自：102/12/21下午由舒宇宸老師在臺大應力所國際演講廳所主講之「醫學影像中的數學」的演講內容

 延伸閱讀：臺大科學教育發展中心探索基礎科學講座2013年12月21日第八講〈醫學影像中的數學〉全程影音

責任編輯：Vita Chen