【大宇宙小故事】26 花拉子模與花拉子米
撰文|葉李華
「中世紀」一般是指公元五世紀到十五世紀,和歐洲的「黑暗時代」幾乎重疊。
然而在世界其他角落,這一千年的時間並不一定黑暗,甚至剛好相反。比方說,其中至少有一半的歲月(八至十三世紀)公認是伊斯蘭世界的黃金時代,這和伊斯蘭教的傳播以及阿拉伯帝國的興衰有著密切關聯。
在這五百多年間,伊斯蘭學者不但保存了險些失傳的希臘羅馬文明,還做了不少錦上添花的工作。因此至今為止,在許多科學領域(包括天文、數學、物理、化學,乃至生物學和醫學)都有伊斯蘭文化的影子。
為了避免長篇大論,讓我們從一個重要個案談起。

●花拉子模
花拉子模(Khwarezm)是個古老的地名和國名,如果你對它有些印象,很可能是因為你還記得成吉思汗西征的歷史(十三世紀初,蒙古第一次西征,滅中亞大國花拉子模)。
而在數學史上,有一位重量級的人物花拉子米(Muhammad al-Khwarizmi, 780?-850?),顯然和花拉子模有些淵源。事實上,他的名字應該譯為「花拉子模的穆罕默德」才算不失原意,正如「李奧納多‧達文西」的正確解讀是「文西的李奧納多」。
這位九世紀的數學家雖然赫赫有名,卻沒有人知道他長得什麼樣子,基於當時的宗教禁忌,他生前並未留下任何肖像。話說回來,名字只是一個代號(稱他為XYZ也無妨),容貌也只是膚淺的表象(後人愛怎麼畫都行)。真正重要的是,我們可以斬釘截鐵地說,他在數學史上有著世界級與世紀級的地位。
這麼重要的人物,當然應該對他的生平多做些瞭解。
●兩種文化
黃金時代的伊斯蘭世界主要成員包括阿拉伯人和波斯人,花拉子模這個國家屬於後者。但由於本文的主角後來定居巴格達(當時阿拉伯帝國的首都),而且他的著作一律以阿拉伯文寫成,以至很少有人留意到他其實是波斯後裔。
從故鄉來到巴格達之後,花拉子米任職於「智慧宮」這個國家級翻譯兼研究機構,擔任類似高級研究員的工作。
「智慧宮」的前身是國家圖書館,藏書自然十分豐富,不但有來自世界各地的經典名著,而且都有阿拉伯文譯本。在這種得天獨厚的機緣下,花拉子米得以同時接觸兩種風格迥異的數學文化──偏重邏輯與幾何的希臘數學,以及偏重計算與符號的印度數學。
由於時間和空間的雙重阻隔,這兩種數學始終沒有接觸的機會。直到這個時候,在花拉子米的大腦中,兩者才首度激盪出火花。
這個火花,就是如今所謂的「代數學」。
●代數學與演算法
大約在公元820年的時候,花拉子米寫出史上第一本代數教科書。由於當時還沒有代數(學)這個名詞,所以他用《移項與消去(的計算法簡介)》當作書名。
在這本書中,花拉子米詳細討論了某些一元二次方程式的解法(所以要用到「移項」和「消去」)。有趣的是,雖然它是標準的數學書,卻沒有任何公式或符號,全書從頭到尾都是文字,頂多再搭配幾張插圖。(頗類似中國古代的數學著作,例如《周髀算經》或《九章算術》。)

你一定學過如何用「公式法」來解一元二次方程式ax2+bx+c=0, 請想想,如果要你完全用中文來敘述這個公式(例如稱x為未知數,稱a為未知數平方的係數),是不是雖然很麻煩,實際上並不怎麼困難?
而且,你很可能曾經使用「電腦看得懂的語言」一步步敘述過這個公式。因為不論多麼巧妙的公式,如果要請電腦代勞,就必須按部就班跟它溝通。比方說,開根號的運算通常只對正數或零有效,填入負數就會出現錯誤訊息,因此你必須根據b2-4ac是否小於零,分成兩種情形來處理。
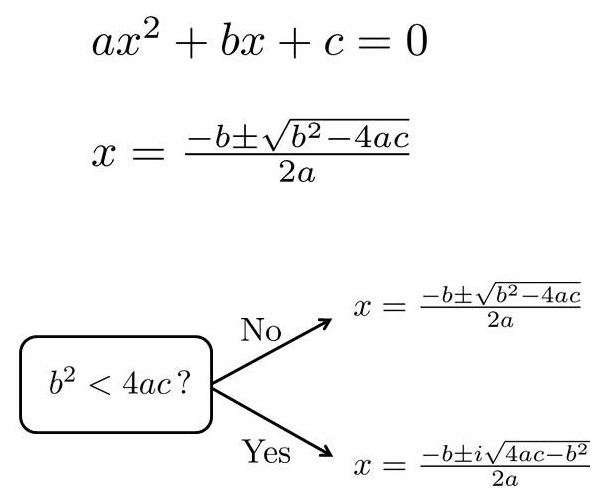
這些按部就班的步驟可以稱為程式,更精準的名稱則是「演算法」(algorithm)。但如果我們採用直譯,這個名詞應該譯為「花拉子米法」,因為在《移項與消去》的拉丁文譯本(1145年),作者的名字被轉換成拉丁風格的Algoritmi(al-Khwarizmi則是直接轉寫自阿拉伯文)。現在,你會不會覺得對本文主角有些親切感了?
事實上,就連「代數」(algebra)這個名詞也是源自這本書,它對應於「移項」的阿拉伯文(al-jabr, 其中al是定冠詞)。
所以說,今後你再碰到al開頭的英文,會不會忍不住懷疑它源自阿拉伯文?(其實機會的確很大,例如alchemy, alcohol, alkali, although not always true.)
●實至名歸
嚴格說來,一元二次方程式的解法並非花拉子米首創,在他之前兩百年,印度數學家婆羅摩笈多(Brahmagupta)就曾經著書立說,詳細討論類似的演算法,而且花拉子米很可能讀過這本名為《婆羅摩曆算書》的印度數學名著。
可是「代數學之父」這個頭銜卻被花拉子米搶了去,從來沒有人為婆羅摩笈多伸冤,這當然是有原因的。對婆羅摩笈多而言,他真正感興趣的是算術和數論的問題,方程式只是解題的工具而已。花拉子米則不然,在《移項與消去》這本書裡,方程式的解法從頭到尾都是主角。
不過千萬別以為花拉子米輕視算術,事實上,他還有另一本傳世之作,書名是《印度計算中的加減法》。這本書最重要的貢獻,就是把「印度數字系統」引進阿拉伯文化圈,然後再經由它的拉丁文譯本,將這個數字系統推廣到全世界。
值得一提的是,「印度數字系統」和「印度阿拉伯數字系統」嚴格說來不能畫上等號,因為後者多了伊斯蘭數學家的一點創意──小數點,更精確地說是「小數點的概念」,因為最初的小數點其實是「個位數上的斜槓」。(不過,由於這個發明來得較遲,花拉子米來不及將它寫進書中。)總而言之,從「印度數字」演變到「印度阿拉伯數字」,過程中也有一個錦上添花的小插曲。
●黃金因素
如前所述,伊斯蘭世界有著長達五百多年的黃金時代,在許多方面都有相當輝煌的成就。我們從花拉子米的個案,至少能歸納出三個「黃金因素」。
一、隨著伊斯蘭教的傳播,阿拉伯文成為共通語言:正如當今的英文(通行全球),以及牛頓時代的拉丁文(通行歐洲),在當時的伊斯蘭世界,阿拉伯文是知識界的共通語言。不論是來自何處的學者,只要懂得阿拉伯文,彼此就不會有語文上的隔閡,這對學術交流有莫大助益。另一方面,花拉子米雖然是波斯人,卻未曾留下波斯文手稿,正是因為波斯文並非當時的主流語言。
二、阿拉伯帝國的首都巴格達是政治兼學術中心:許多學者不遠千里而來(包括歐洲人與中國人),花拉子米就是代表人物之一。這麼多優秀的學者聚在一起,自然形成一股強烈的學術氣氛。
三、智慧宮主導的百年翻譯運動功不可沒:花拉子米就是最好的例子,他根本不必學習希臘文或梵文,便能研讀希臘數學與印度數學的經典,例如前述的《婆羅摩曆算書》。
註一:阿拉伯帝國是標準的政教合一政體,統治者稱為「哈里發」。花拉子米之所以來到巴格達,很可能是受邀於當時的哈里發──馬蒙(Al-Ma'mun, 786-833)。馬蒙於在位時期(813-833)大力支持翻譯運動與學術研究,智慧宮就是在他手中由圖書館蛻變為國家級研究機構。
註二:公元1258年,智慧宮毀於蒙古第三次西征,藏書通通被拋到底格里斯河中,造成「墨流成河」的奇景。隨著巴格達的陷落,伊斯蘭世界的黃金時代也就此落幕。
註三:在許多文獻中,代數學之父這個頭銜由花拉子米與古希臘數學家丟番圖(Diophantus)共享。事實上,丟番圖和婆羅摩笈多一樣,僅將方程式當作解題的工具。
註四:在《移項與消去》這本書中,花拉子米僅僅探討「有正數解」的一元二次方程式,因為當時伊斯蘭數學家認為「負數解」並沒有(幾何)意義,而複數的出現則是幾百年後的事。
註五:在西方文獻中,許多伊斯蘭學者的名字都有兩種寫法,一是直接轉寫自阿拉伯文,二是轉化為發音類似的拉丁名字。正如Matteo Ricci這個名字若譯成中文,可以是「馬泰奧‧里奇」,也可以是「利瑪竇」。
註六:「花拉子模」與「花拉子米」也譯為「花剌子模」與「花拉子密」。花拉子米的阿拉伯文全名是Muhammad ibn Musa al-Khwarizmi, 其中ibn一般來說意指某人之子,亦即Musa是花拉子米的父親(但也有可能是某位重要的祖先)。
