玩21點破解莊家優勢的方法:量子糾纏
編譯/台大物理系學生 楊泰萱
21點的規則中,即使個人按照最佳策略玩,莊家優勢仍有0.6%,表示我們平均每下注1000元會賠6元,然而如果玩家們可以合作並溝通,我們便可讓第一個人下注極少量以獲取資訊,再用記牌的方式算出剩下的期望值決定加牌與否或是下注的大小。這種合作記牌曾經在1979年被麻省理工學院、加州理工學院、哈佛大學的學生成功使用,他們後來也變成賭場的黑名單,而這則故事也在2003年被翻拍成電影:Bringing down the house。
然而如果玩家間如果不能直接傳遞資訊,那上述的記牌方法便不可行,但麻省理工學院以及加州理工學院的學生想出一套利用量子糾纏的特性,讓即使兩個玩家之間只能傳遞1個位元的資訊(即決定「加牌」或是「不加」),也能擊敗莊家優勢。而讓此方法能成功的原因正是量子位元可以產生糾纏的特性。與一般古典位元只能表示0與1不同,量子位元可以是0與1的疊加態;更有趣的是,兩個以上的量子位元間還可以有糾纏(entanglement)的關係,也就是一個量子位元測量後的結果會影響其他的量子位元。一個量子位元疊加態的例子如下:
![]()
我們可以在此例中可以觀察到這個量子位元為0和1的疊加態,只有在我們最後觀察時,量子位元才會根據機率塌陷成0或是1,另外一個例子是兩個位元的疊加態如下:
![]()
假設有一個兩個位元的量子態為|ψ⟩,當我們對第一個量子位元做測量,如果得到的結果是0,則得到的這一瞬間,第二個量子位元也會自動變成0;如果得到1,則第二個量子位元也會自動變成1。
在21點的規則中,莊家先發給每個玩家以及他自己1張朝上且大家都可以看到的牌,再個別發給玩家一張蓋住只有該玩家自己可以看到的牌,每個玩家可以根據他們被發到的兩張牌決定要「加牌」還是「不加」。如果玩家加牌後牌的點數總和超過21點,就會失去他們的賭金。在玩家全部都加完牌之後,莊家會決定要不要幫自己加牌,如果莊家加牌加到自己的牌點數總和超過21,則尚未失去賭金的玩家們就可以贏得莊家的賭金;若莊家沒有加超過21點,則莊家與玩家會比他們手中撲克牌點數總和的大小,點數大者贏得賭金;點數相同則各自拿回賭金;點數小者失去賭金。
總結來說,可以把21點的情況分為以下三種可能:
1.玩家失去賭金莊家獲勝:玩家在加牌時點數總和超過21點或是玩家最後與莊家的點數進行比較時點數小於莊家。
2.玩家與莊家各自拿回賭金:玩家最後與莊家的點數進行比較時與莊家點數相同。
莊家失去賭金玩家獲勝:玩家最後與莊家的點數進行比較時比莊家點數大,或是自己加牌後點數總和不大於21但莊家加牌後點數總和大於21
其中撲克牌2~9牌點數分別為2~9,10、J、Q、K點數都為10,而A可以依據情況當1或當10。
在該篇論文中,假設玩家僅有兩位,且第一位玩家Alice下注量為0,Alice的任務是利用他加牌或不加的選擇,傳遞資訊給第二位玩家Bob,學者們先把兩個玩家的行為:「加牌」或是「不加」,對應到量子位元測量後為|0⟩或|1⟩的結果;而自己手上的牌以及蓋住的牌會決定如何對該量子位元進行操作,而再利用上述量子位元的特性,設計出一套可以擊敗莊家的方法。其設計出的量子電路如下:
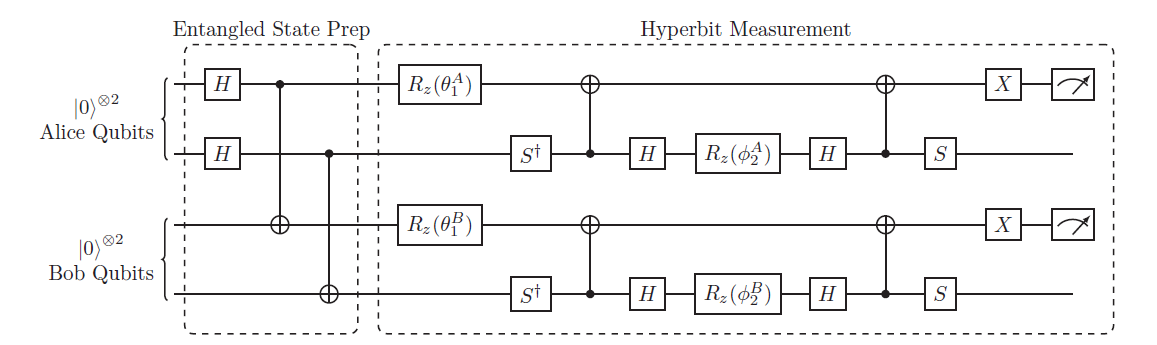
其中第一個框框的用途目的是讓Alice跟Bob之間的量子位元產生糾纏的特性,而第二個框框(Hyperbit measurement)可以理解成Alice和Bob分別依照他們手中的牌對量子位元進行操作,再按照最後的測量結果決定要加牌或是不加。而研究人員證明在經過約幾千輪的遊戲過後,Alice和Bob相比莊家可以取得一微小的優勢。
雖然此方法目前只適用於兩個玩家的情況,且也僅在牌庫中的牌剩下八張以下時才被證明可以破解莊家優勢,但我們仍可以藉由此項發現看出未來量子資訊領域的潛能。此論文的作者之一,也是提出在量子計算領域重要的HHL演算法的Aram Harrow說道:「訂定21點規則的人並沒有想到量子糾纏,可是當每個玩家被發到牌的時候,他們的牌之間一定會有某些相干的性質,那這可以用量子位元糾纏的特性來描述嗎?」而另外一位作者Joseph A. Formaggio也有趣地回憶到:「我非常感謝在我當時提出這個想法的時候,他們(Joseph Lin, Aram Harrow)沒有嘲笑我,而是關起門來認真跟我討論這個問題」
最後,這個方法未來可以延伸到當牌庫有更多牌的時候嗎?抑或是賭場需要擔心有人用此方法破解莊家優勢嗎?「如果要讓這個方法在賭場中實現,你可能會需要在你的包包裡放一台量子電腦來算這些牌局上的變化,但這目前基本上是不可能的,所以我覺得目前賭場還不需要擔心這些事情」而筆者個人認為在可能10-15年後具有能實現秀爾演算法 (Shor’s algorithm) 的量子電腦誕生之際,把量子電腦的特性用在賭場上也不失為一種可能,賭場可能也要像其他網路大公司一樣,要想出一套新的加密方式(21點規則)去確保莊家優勢不會被量子電腦破解。
參考資料:
- Blackjack: Can a quantum strategy help bring down the house?, 2020.8.3
- Joseph X. Lin, Joseph A. Formaggio, Aram W. Harrow, Anand V. Natarajan. Quantum blackjack: Advantages offered by quantum strategies in communication-limited games. Physical Review A, 2020; 102 (1) DOI: 1103/PhysRevA.102.012425
- How Quantum Entanglement Can Help You Win At Blackjack, Elizabeth Fernandez, 2020.6
