讓你不迷路的萬能地圖
撰文|賴加翌
我想大家都有這樣的經驗:和朋友約在一個地點見面,但他卻在附近迷了路,最後只好打電話給你,告訴你當下的位置請你指路。但是如果人在國外就比較麻煩了,他可能看不懂路標和店名。
這時候,如果當地的街道都被染成特定的顏色,他只要按著固定的模式走就能到目的地,那不是方便嗎?你可以在電話裡跟他說:「沿著藍色那條路走到交叉口之後,換走紅色那條,再走到下一個交叉口時,繼續走紅色那條。紅色走完接藍色,藍色一直走到交叉口換紅色,紅色走到一個交叉口繼續走紅色,這樣就可以到了。」講白一點就是說,他只要不斷照著「藍—紅—紅」的模式走下去,就算他不清楚自己現在哪裏,最後還是能到指定地點。
或許單純用說的很難想像,不如直接看下圖。按照「藍—紅—紅」的模式重複三次,不管你人在哪裏,都能到黃色的點;而按照「藍—藍—紅」,的模式重複三次,則一定會到綠點。
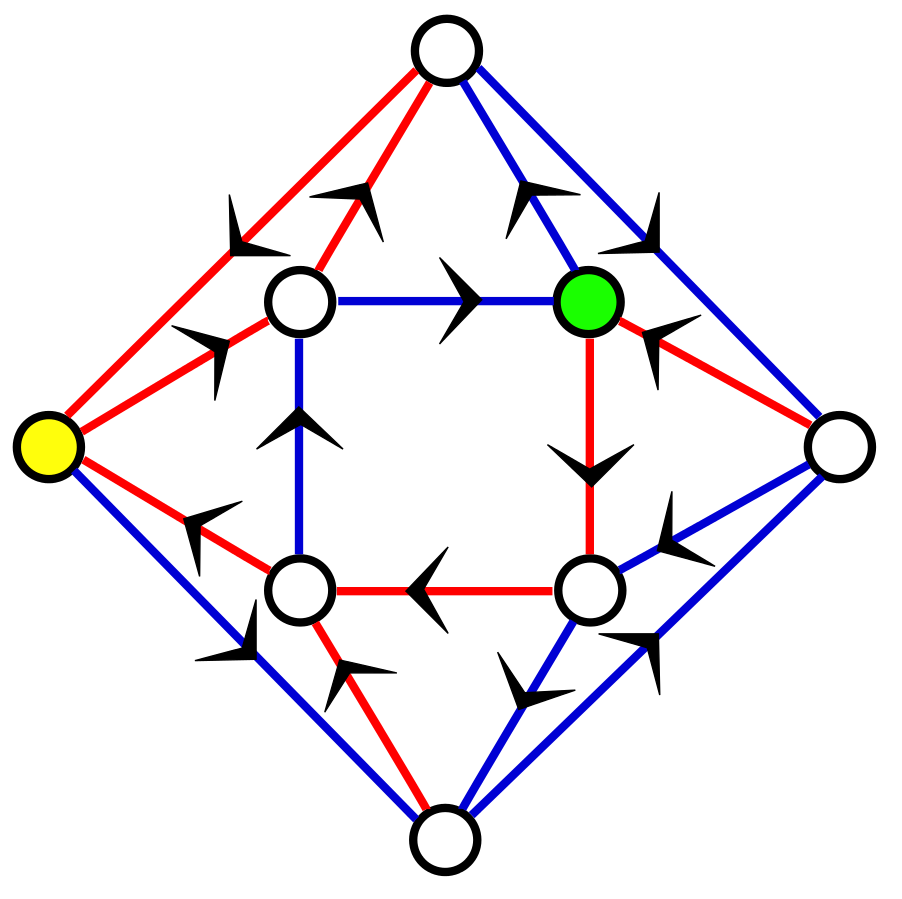
道路著色的問題,是圖論中非常有名的問題之一。由節點和連接節點的邊所構成的圖形,可以衍伸成現實世界中遇到的系統。比如街道的交叉口可以看做是節點,而街道看成是邊。網際網路的世界裡,節點就是路由器,邊是路由器之間的連結。以航空網路來說,節點就是機場,而邊是機場到機場之間的航程。
令人好奇的是,每個點和邊構成的圖形都存在像這樣理想的「萬能地圖」嗎?只要將邊上色,就可以照著簡單重複的指令到達目的地?1970年班傑明.懷斯和羅伊.阿德勒最早提出這個問題,本來只是要找地圖,順便想到要設計一個電腦的自動除錯程式。想不到自己提出的問題,花了好幾年還沒辦法證明。因為這個想法相當有趣,引起一些數學家的關注,前前後後出了幾篇相關論文。
雖然問題的敘述看似單純,卻在數學界懸而不解將近40年,直到阿夫拉罕.塔克特曼出現,他證明任一個點和編構成的圖形只要完成某些特定條件,都能以「萬能地圖」般的方式著色。這個證明不只是數學上的成就,在計算機領域也有特別意義。等於是說明了某些情況下,錯誤數據和干擾不影響結果,就像迷路的朋友就算不知道自己位置,只要依據重複指令,都能到達目的地。
參考資料:
- Vojtěch Vorel, &Adam Roman. Complexity of road coloring with prescribed reset words. Journal of Computer and System Sciences. 2016
- A.Roman, &M. Drewienkowski. A complete solution to the complexity of Synchronizing Road Coloring for non-binary alphabets. Information and Computation. 242, 383-393. 2015
