v=5/2 量子霍爾態之謎(上)
■v=5/2到底發生了什麼事?這是研究霍爾效應的學者們近年來最關切的問題之一。
撰文|蕭維翰
筆者曾用了三四篇文章來討論霍爾效應。從經典的整數量子霍爾效應(IQHE)、分數量子霍爾效應(FQHE)、複合費米子(Composite Fermion)到最近重新掀起討論的 v=1/2費米液體態(Fermi Liquid)。在本文中筆者想延伸這些故事,討論另一個實驗上被觀測到的著名的偶數分母的量子霍爾態—— v=5/2,以及它所牽涉的謎團。
然而筆者必須先在此自白:量子霍爾效應並不算是最好的科普題材。儘管這個問題的組成元素很基本:電子、庫倫作用與垂直的磁場。但真的要進行定量說明的時候,我們很難避免討論一些比較生硬的概念,比如說磁通量附著(flux attachment)與測試波函數(trial wavefunction)。而且事實上除了一些拓樸性質,譬如電導率的係數 v,即便最前沿的計算也很難給出很好的解析結果。絕大多數我們必須倚賴數值計算,從而失去一些直覺。
從實驗的角度,從事量子效應測量的團隊在世界上也非大宗。
然而,從理論物理學歷史的角度看,量子霍爾效應卻與很多點子的誕生與發展密切相關,包括拓樸超導體、陳-西蒙斯(Chern-Simons)理論、馬約拉納費米子(Majorana fermion)、對偶(Duality)等。也因此,當代的理論物理學家們儘管未必是霍爾效應的專家,但或多或少都會對它的特徵有些基本的認識。
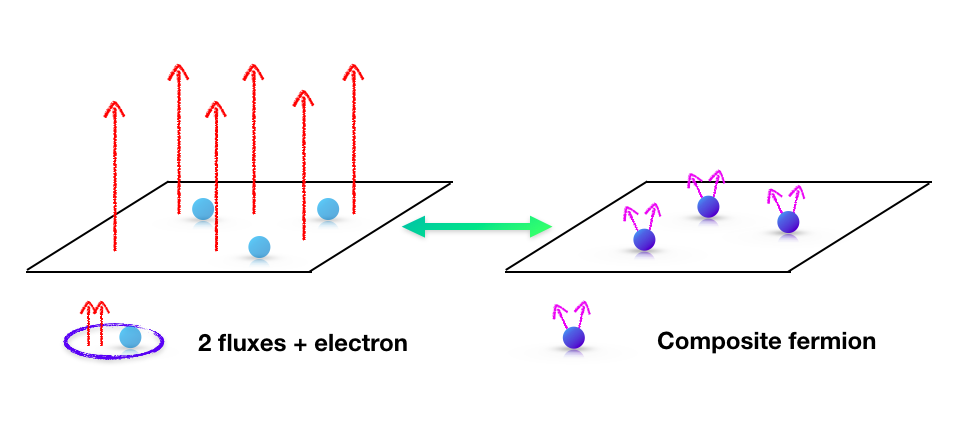
●量子霍爾效應
現在讓我們先用 30 秒複習量子霍爾效應的基本物理。
首先忽略電子之間的交互作用,那麼電子能階在磁場中會形成蘭道階(Landau Levels)。每個蘭道階就像一層公寓,有很多具有一樣能量(房租)的軌域(房間)。當電子恰好填滿某個數目的蘭道階,想要到達下一層樓就必須支付能量(加錢)。因而整個系統內部形成一個絕緣體。當在 x 方向施加電場 Ex ,我們其實沒辦法激發出 x 方向的電流,但在系統的邊界累積的電荷可以導致 y 方向的電流 Jy,寫成歐姆定律的形式:
![]()
而這邊的霍爾電導是整個霍爾效應裡最重要的物理量,它符合量子化的條件
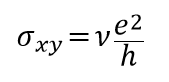
其中v代表了被填滿的蘭道階數目。
而後人們在實驗中發現v 其實也可以是個分數,而前面的論述無法說明分數的量子霍爾態。R. Laughlin 首先提出了一個測試的波函數,很好地描述了v=1/3的性質。在物理圖像的理解上,J. K. Jain [2] 提出了複合費米子的概念,將一個電子解釋成一個複合費米子加上兩個單元磁通量,而分數的量子霍爾效應便能夠理解成複合費米子的整數霍爾效應。
若複合費米子處於整數霍爾態n, 而電子處於分數霍爾態v,他們的關係可由所謂的 Jain 序列給出:
![]()
其中在n→∞ 的極限,v趨向 1/2。在這個極限複合費米子感受不到任何磁場,而直覺上這會形成一個費米海( Fermi Sea)與金屬態。從多體物理的角度而言,這個費米海是沒有能隙的,也就是說無窮小的能量便能激發這個系統,而這也被實驗所證實。
●v=5/2 態
奠基在這些背景知識,在接下來的篇幅,我們就解釋v=5/2 的神秘之處,並且在續作中嘗試鋪陳與其相關的謎團。
首先我們希望透過小學加法先建立一點直覺:
5/2=1*2+1/2
這個解析的意思是,v=5/2的量子態是兩個滿的蘭道階與一個半填滿的蘭道階。由於填滿的蘭道階和半滿的蘭道階之間有能隙,這個能隙的大小正比於磁場,從而在磁場很大的狀況下,低能量的物理應該只跟半滿的蘭道階有關係。沿用前一段的論述,我們的直覺是這個量子態應該也要是個金屬態。
然而有趣的事實是,實驗上所見的v=5/2與 v=12 不同。前者具有霍爾平臺,並且是個有能隙的量子態。
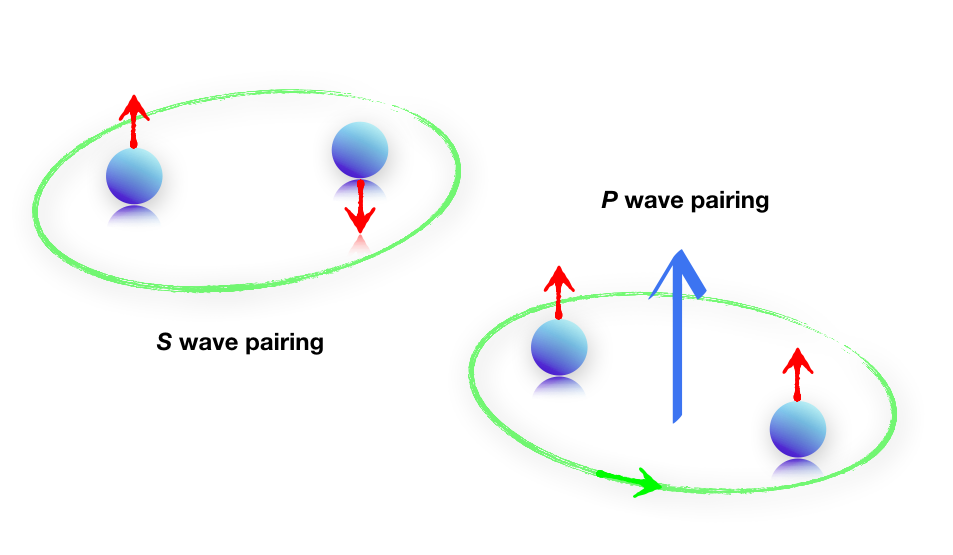
所幸,這不是物理學家們第一次遇上一個無磁場的費米海形成有能隙的量子態。超導體基本上就符合這樣的特徵。爰此,目前 v=5/2 被廣泛接受的理解是,複合費米子們形成古柏對(Cooper pair)而凝聚成一個超導體態。但這個古柏對不可以是最簡單版本的 BCS 模型。因為在強磁場中電子們的自旋方向被極化,儘管複合費米子看不見磁場,但因為它們跟電子們具有一對一的對應,也就沒辦法形成自旋向上搭配自旋向下的 s 配對。由於庖立不相容原理,只能是具有奇數角動量的 p, f, ... 配對。
這個解釋提供了物理圖像,但真要進行計算時,我們想要知道這個系統基態真正的長相。退數步言,我們想知道有沒有一個像 Laughlin 波函數一樣的測試波函數,既可以寫出(不算太複雜的)解析形式、具有正確的拓樸性質(量子數)並且在數值上十分靠近真正的基態?
簡單的答案是,還真的有,而且有太多了。在下集中,我們將介紹一些有力的候選人、他們所具備的特徵,並且指出近來的實驗新發現如何對影響物理學家們對它們的態度與點子。
參考資料:
[1] R. B. Laughlin, Phys. Rev. Lett. 50, 1395 (1983).
[2] J. K. Jain, Phys. Rev. Lett. 63, 199 (1989).
--
作者:蕭維翰,臺大物理系畢業後逃到芝加哥,吹風吹雪之餘,做研究讀博士班。可惜離開臺灣後無海可看,只能在密西根湖旁揀一方堤岸,偽裝成看海的人。科教中心特約寫手,從事科普文章寫作。
