可能的新物質相（一）：靜電學的啟示

■物理學家致力於探索物質的相的終極可能性。而近年來的「fracton」是一類嶄新，還不確定如何分類的相。

撰文｜蕭維翰

這個開頭已經老套得讓筆者有點羞愧，然而，我還是必須重申，對於物質的「相」（phase）的可能性一直是固態、凝態物理學家所在意的大課題之一。或許對於一般讀者更重要的事情是，這類研究的起源是與生活息息相關的。最簡單的例子包括回答冰與水之間的差異、鐵和磁鐵間的區別。從而也不難想像，這類從生活中獲得許多提示的問題，遠在 1930 年代，便有蘭道（L.D.  Landau）[1] 等大人物解決了。

到了 1980 年代，人們發現有一些系統的相沒有辦法用前述的典範式概念去區分。最具體而易懂的例子是量子霍爾效應，在這種系統中，不同的霍爾態是由霍爾電導的係數去決定，但每個態都是一種「量子液體」（quantum liquid）過去二、三十年，許多物理學家便致力於定義新的相去歸類所有可能的量子狀態，有興趣的讀者可以去搜尋關於拓樸相（topological phase）的文獻 [2]。

然而，相的分類學卻沒有因為拓樸相領域的成熟而完結。最近這幾年，物理學家又陸續發現了一些新的模型，其中某些物質態超越了雙雙蘭道典範與拓樸相的界定範疇，有一類這樣的系統叫做 fracton^[1] [3]。儘管在實驗上，這些模型是否能夠被實際地創造出來還是未知數，但學理上要完備所有可能的物質相，勢必還需要一點努力。

筆者曾經很猶豫是否該貿然介紹這類發展中的概念，尤其在連一些較成熟的物質相概念都還未讀者介紹前，就希望大家能感受到其中的差異。

直到這幾日，筆者發現了 fracton 的維基頁面，且基於之前的閱讀經驗，覺得這些系統的某些概念或許較拓樸相更直覺一點，因此決定冒險使用兩篇文章來介紹這個非傳統的物質態。

說了這麼多，究竟什麼是 fracton？或者說，當一個「電荷」具有什麼特性時，我們會叫它 fracton？受限於筆者的知識與該領域的新穎，筆者很難寫下一個嚴格的定義來描述這件事。但我們知道一些特徵：如果一個系統裡面有一些「粒子」，當它獨自存在時，完全沒辦法在不創造其他粒子的狀況下移動它，或者只能在某個維度移動的時候，我們稱呼它為 fracton。

儘管 fracton 最初是出現在一些很特殊的模型上，這兩年來物理學家們發現在一些跟電磁學很像的物理理論中的「電荷」具有 fracton 的特性 [4]。在剩下的篇幅，筆者就來談談一些高中電磁學程度的概念，並由這些概念演繹出一些不困難，但不常被強調的概念。

讓我們回憶高三物理或者大一普通物理下。在靜電學的單元中，我們知道若有人把一些電荷包在一個很大很大的黑盒子中，原則上就算看不見盒子內部的細節，我們也可以知道盒子內的淨「電荷」有多少。這是因為電荷的高斯定律說，盒子內的電荷量正比於整個盒子的電通量。是以即便只有盒子表面的電場資訊，我們也能計算電通量然後得知內部的電荷總和。

這個論述，是跟盒子大小無關的，比如說，我們可以將所有電荷集中在半徑一公分的球體裡面，然後分別在半徑十公尺與十公里的球殼表面計算電通量，所獲得的計算結果都要一樣。

這意味著，如果我們有一群小天使可以，也僅可以改變半徑一公分的球內的物理狀態，更明確地講，他們可以創造或摧毀這局部的電荷，高斯定律告訴我們的是，這群小天使所做的任何改變都無法改變淨電荷數。因為我們的前提限制了他們無法改變半徑一公分外的世界，但淨電荷的量可以透過計算半徑十公里處的電通量得知，只要這表面上的物理狀態沒有被改變，內含的淨電荷也就必需維持不變。

換一句比較像高中老師的話說，由於電力線終止（或起始）於無窮遠處，任何局部的操作都沒辦法摧毀或生成新的電力線。而點電荷，雖然看起來只是一點，但卻不是一個局部的物理物件。

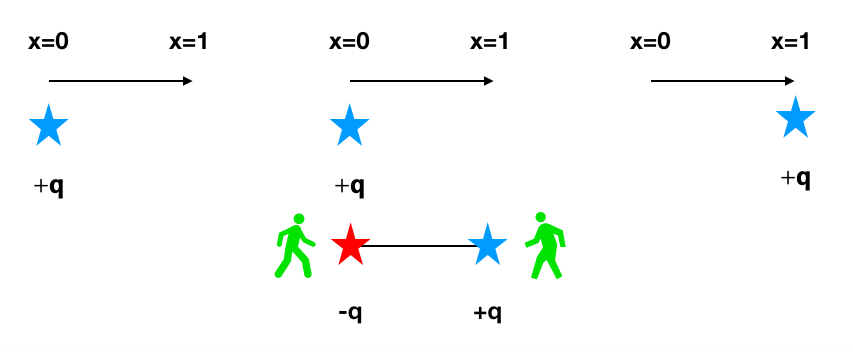
但這群小天使可以創造電偶極而不違反高斯定律，也就是一次創造兩堆相同電量但電性不同的電荷。這樣的自由度使得單一的電荷可以透過局部的操作自由移動。舉例而言，若我們想要把一個在 x= 0 的電荷 +q 往右移動，我們可以通知小天使們創造一個電偶極 p，其中 -q 在 x= 0 而  q 在 x = 1，透過將這個電偶極作用在原先的電荷上，它就像從 x= 0 移動到 x= 1 一般。

在下半集中，筆者將解釋，基於同樣的物理論述與圖像，當我們推廣高斯定律到電偶極甚至其他種類的電荷上時，這些「基本電荷」的行動能力將會受到很大的限制，而某些例子便具有 fracton 的特徵。

參考資料：

[1] L. D. Landau, and E. M. Lifshitz, Statistical Physics Part 1, Course of Theoretical Physics Vol. 5, 3rd Ed. (1980).

[2] X-G. Wen, Quantum Field Theory of Many-Body Systems (2004).

[3] R. M. Nandkishore, and M. Hermele, Fractons, arXiv: 1803.1119

[4] M. Pretko, Phys. Rev. B 95, 115139 (2017).

 

註解^[1] 筆者不是故意不寫中文，因為這個名詞新到還沒有（廣為接受的）切確中文翻譯。

--
作者：蕭維翰，臺大物理系畢業後逃到芝加哥，吹風吹雪之餘，做研究讀博士班。可惜離開臺灣後無海可看，只能在密西根湖旁揀一方堤岸，偽裝成看海的人。科教中心特約寫手，從事科普文章寫作。