電導率、弱局域化、與量子混沌（下）

■在上文中我們提及，物質波間的干涉會減弱系統的電導率，在本文中我們討論混沌現象（Chaos）[1]如何對這個減弱這個局域化的效應。

撰文｜蕭維翰

回顧前文，我們對於計算固態系統中電導率的方法稍作了討論，指出 Drude 圖像給出古典的計算結果。然後我們討論次一階的量子修正，說明在某些路徑上傳遞的物質波可以建設性干涉，放大粒子在運動時回到原點的機率，等效而言增強電阻、削弱電導，此現象稱為弱局域化（weak localization）。

從時間尺度來看，Drude 圖像中有一個弛豫時間（relaxation time）對應散射間平均時間間隔。弱局域化問題中有一個相干時間（coherence time）用以標明物質波失去相干性需要的時間長度。

另外我們也有空間尺度，弛豫時間乘上費米速度定義了平均自由徑（transport mean free path），是「有效」散射之間平均的空間間隔[2]。物質波的波包大小可用德布羅伊波長代表。所謂的準古典，意指後者比前者小得多，所以物質波看起來跟粒子相異不大。

在本文中，我們將討論另一種對電導的修正，以及它所對應的時間尺度。

從前文到現在，我們一直說帶電粒子可以跟晶格、雜質碰撞跟散射，但一直被遮起來的訊息是這些東西的特徵，比如說他們的大小。事實是前述的計算大多是考慮點狀的雜質，也就是遠小於物質波波包大小的尺度，這個假設的好處是我們很清楚擴散方程式的解，所以可以計算出一些乾淨的答案。倘若這些與粒子散射的物體比波包大得多，擴散方程得到的解是有疑慮的。

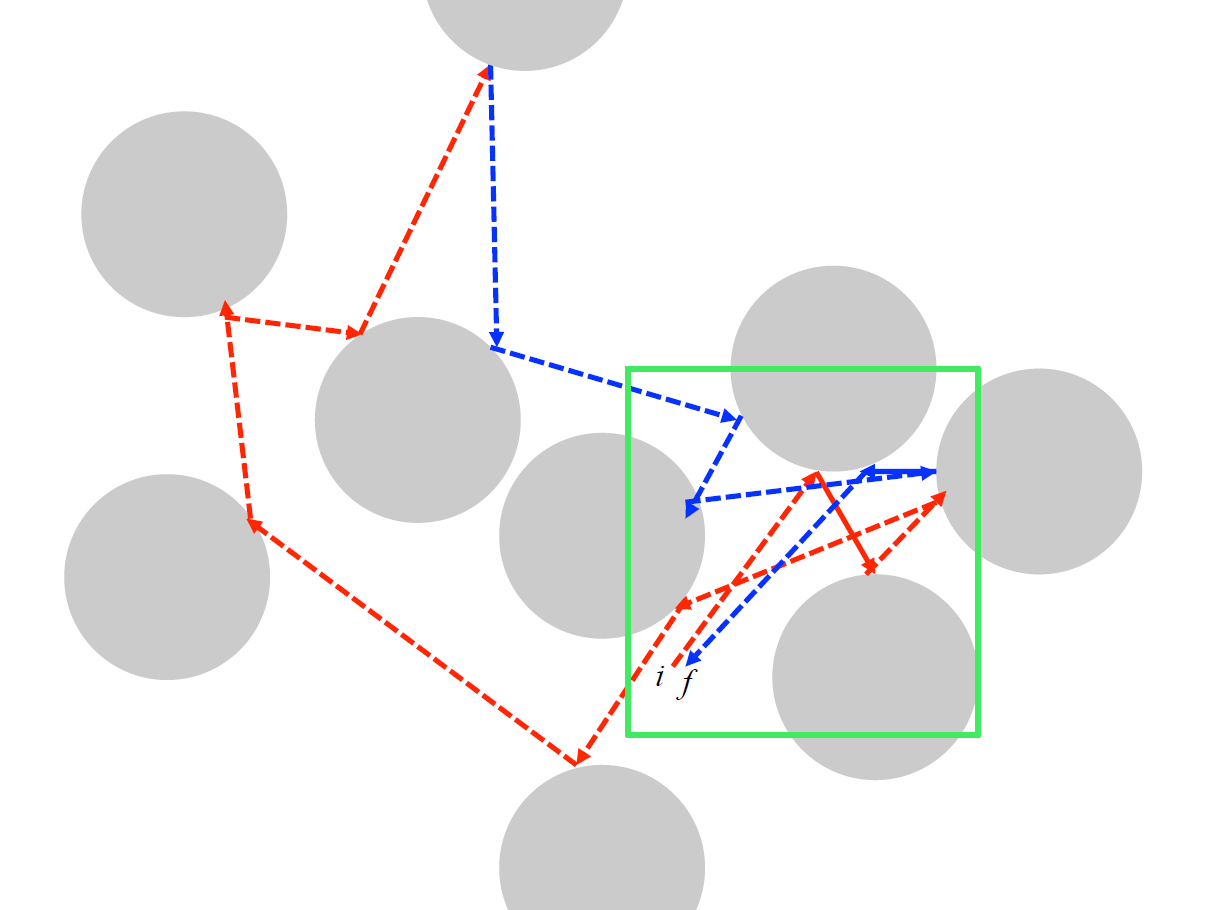
更精確地說，在擴散方程式中一個假設是沒有記憶效應，也就是粒子在運動過程中可能跟同一個物體發生過很多次碰撞，但這些碰撞被視為獨立事件。當這些散射體很大的時候，粒子的物質波包運動看起來就像古典粒子，我們可以考慮一種過程，即初速度與末速度反平行，但初位置與末位置只差一點點（如圖一所示）。這種運動的初段與末段，處於幾乎一樣的環境中，依循幾乎一樣的軌跡，似乎沒什麼道理說這兩段是無關聯的，這便是擴散假設的不適用處。

從另外一個角度看，我們有兩條路徑，一個從初位置出發（圖一中紅虛線），一路經過很長的時間帶著與初動量反平行的末動量來到末位置，第二條路徑（圖一中藍虛線）從末位置出發，帶著與前者一路相反的動量來到初位置。這兩條路在一開始時是密切相關的，擴散假設不適用; 直到它們之間的距離比散射體的尺寸大，乃至於到達平均自由徑的尺寸，此後的碰撞可以由擴散方程式描述。

以一句話摘要這個故事：初始條件相似的兩路徑，很快的分離並失去關聯。豈不是所謂混沌現象的特徵？

也因此這邊出現了一個新的時間尺度，叫做埃倫費斯特時間（Ehrenfest time），它正比於散射體大小與德布羅伊波長比值的對數，時間的單位則是李亞普諾夫指數（Lyapunov exponent）分之一。[3]物理上對於這個時間的詮釋是，原本的物質波波包透過指數成長長大成散射體大小的時間。也就是從不適用到適用擴散方程需要的時間尺度。

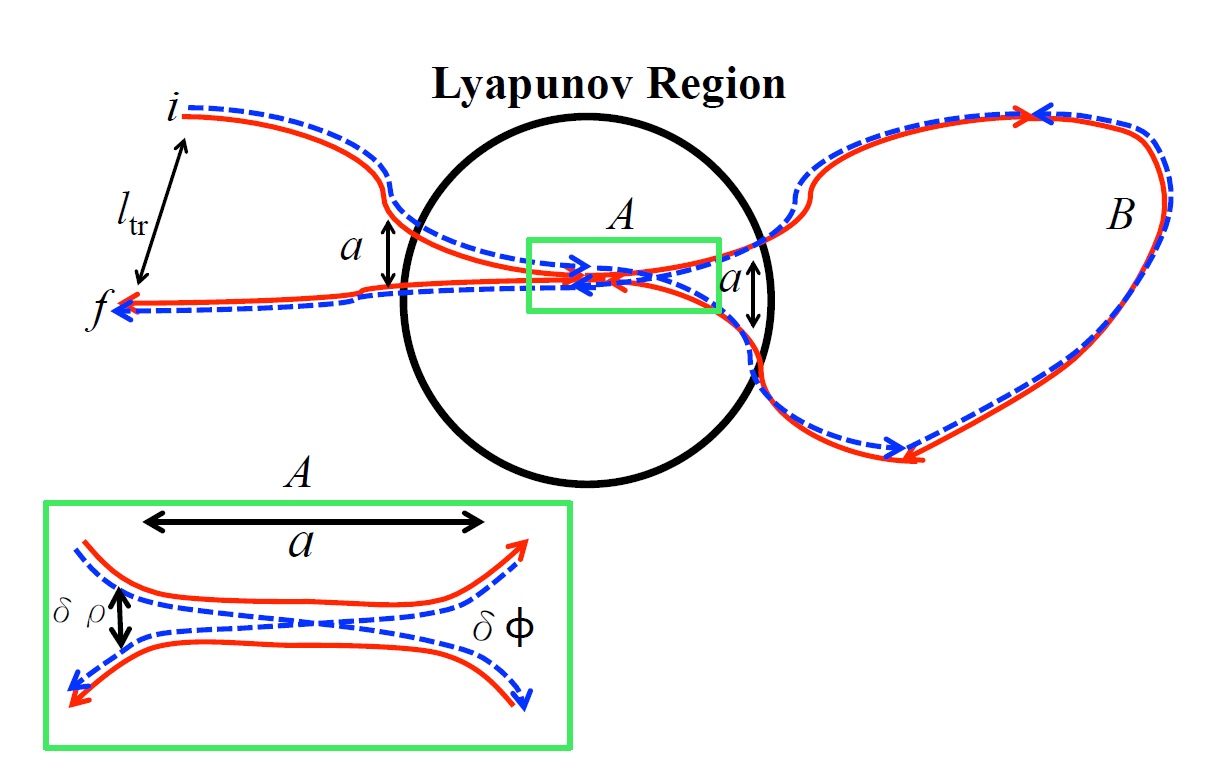
要從這個單一路徑的故事決定電導，回憶費曼說的話，當一個粒子從 i 到 f ，我們必須加總所有可能的路徑來決定機率，如果兩路徑間長度差異過大，則因為相位差異太大基本上不相干，就像在上集中討論的，我們必須找出一些可以建設性干涉的軌跡對，我們將這樣的軌跡（紅色實線與藍色虛線）畫在圖二中，這兩個軌跡幾乎是一模一樣的，只是在 A 處，紅色線跟自己平行而過而藍線與自己相交。使得在 B 區，紅與藍的關係便像是前面兩段討論的兩路徑一樣，而根據上一集的論述，在B區，藍軌跡與他的倒帶版本紅軌跡有建設性干涉。

將這些軌跡的貢獻加總，我們會發現：如果相干時間小於埃倫費斯特時間，則局域化的效果是被減弱的。物理上來說，必須等物質波的波包成長到散射體的大小，弱局域化才會開始顯著，假若在這之前，物質波已經因為非彈性散射失去了相干性，就沒有後續的局域化現象。

現在在介觀物理中，實驗學家已經有辦法設計大散射體尺寸的系統，因為上面的研究與可觀測量電導率直接相關，透過量測，我們有機會去實驗量測在古典系統中不易分析的李雅普諾夫指數。

註解:

[1] 關於混沌的基本概念，也可以回溯探索講座第15期：秩序與複雜的華爾滋。

[2] 有效這兩個字很重要，不然底下讀者可能會覺得明明一直在碰撞跟散射，而感到混淆。

[3] 在混沌問題中，李雅普諾夫指數決定兩軌跡分離的速率，正的值愈大，整個系統對於初始條件愈敏感。

 

參考資料：L. Aleiner, A. I. Larkin, Divergence of classical trajectories and weak localization, Phys. Rev. B, 54, 14423 (1996).

--
作者：蕭維翰，臺大物理系畢業後逃到芝加哥，吹風吹雪之餘，做研究讀博士班。可惜離開臺灣後無海可看，只能在密西根湖旁揀一方堤岸，偽裝成看海的人。科教中心特約寫手，從事科普文章寫作。