【物理世界】量子霍爾效應(一):塵埃中洗滌出的整數
■真的要寫量子霍爾效應,可以寫好幾本書,要從最尖端的進展切入,也會讓讀者摸不著頭緒,這邊我分稿從歷史的起源開始,並只挑一些聽起來真的可以令所有人驚訝的面向。
撰文|蕭維翰
筆者儘管基於工作很常算數學,但上大學後幾乎不常親自動手做數字計算了。前幾個月我在電腦上送出一個滿複雜的積分,幾秒後我得到
-12.56637062125499/(4 π)
不知道讀者們平常做算術的頻率如何,在作業中遇到這種數字會不會覺得很沮喪?分子那一串數字已經無跡可尋,何況底下還除一個 4π?然而有趣是,在電腦有效的位數下,這個組合其實跑出了──
-1.00000000000000
看到這個數字時,我鬆了口氣,撇開在計算前我們已經知道結果的這種經驗談,當你在一連串雜亂無章的數字中翻滾,最後得到了一個至少達14位數精確度的整數──這應該不是巧合,背後理應有什麼法則在規範表象的魔法。
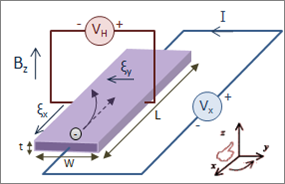
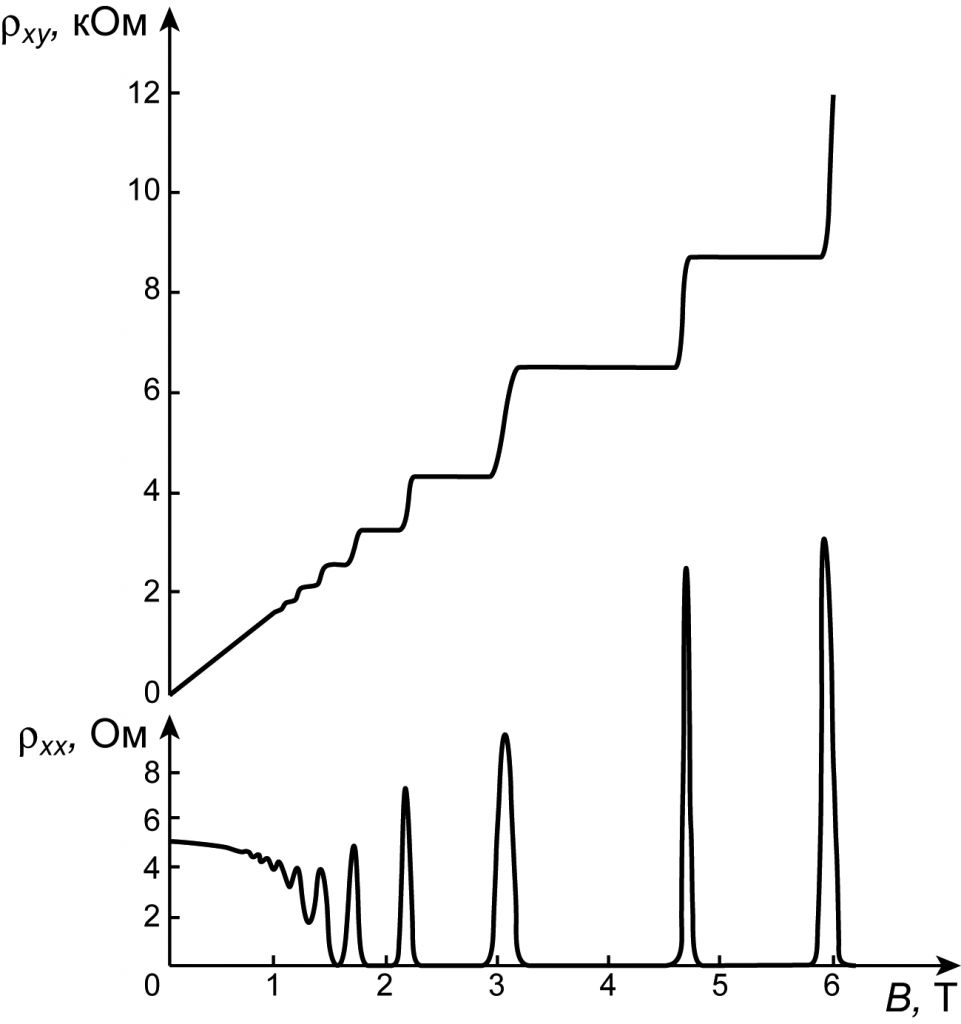
類似的奇蹟也發生在物理的實驗中。設想將一塊平板狀的電晶體放在與樣品垂直的磁場裡,在樣品的長的方向施加電流。我們回想在理化課程中談過,電荷在磁場中感受的磁力總是與電荷速度垂直,也就是說當一個電荷被丟到磁場中,它會轉彎。因而,儘管一開始施加的只是在長方向的電流,但在寬的方向也可以量到電壓差,將寬方向的電壓除以長方向的電流,古典上是一個叫做「霍爾電阻」RH的量,可以用來判定材料中流動電荷的正負號。Von Klitzing 的團隊在 1980 年研究半導體電晶體的霍爾效應時,發現在低溫高磁場的狀況下,霍爾常數、電子電荷 e 與普朗克常數 h 形成的一個比值是整數,而且是極度精確(超過百萬分之一的精確度)的整數,此外,當我們將電阻對磁場作圖時,可以看到明顯的平台結構。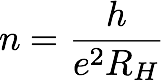
即便今日,我們也沒辦法確定半導體材料中沒有雜質,遑論 30 年前?也因此當科學家發現這樣精確的整數,十之八九是淘到了寶。
在材料內發生的故事可以這麼想像:首先,當電荷初始的速度與磁場垂直且沒有電場時,它的運動模式是繞著一個圓圈轉。所以我們可以進一步想像一塊平板的材料,它的垂直方向被加了磁場,裡面的電荷就都開始轉圈,在量子力學的層次,整個材料好像變成了一個公寓,一個圈圈代表一個房間,裡面住著一個電荷。現在應該沒什麼公寓只有一樓的,在磁場中的材料也是。蘭道(L. D. Landau)指出,這些公寓也有很多樓層,稱為蘭道階(Landau Level),住同一樓的電荷們都有一樣的能量,樓層越高,能量(房租)越高。霍爾測量中的整數,可以對應到住滿的蘭道階數。[註1]
在抽象數學的層次上,被佔滿的蘭道階數目對應到所謂的「陳數」(Chern Number)。我在文章開頭所講提的那些數字,即是某個模型的陳數。(這也是為什麼我看到是 -1.000000000後便安心的去睡覺了。)儘管陳數的由來不是簡單的數學概念,但卻有一個簡單的圖像可以理解它為什麼是整數:設想某個庭院的正中央有一個半徑為 1 公尺的噴水池,有一路人甲從噴水池的某個點出發,繞著水池走了不知道幾圈後回到同一個點,這時候他想知道
全程下來他共繞了幾圈?這個問題顯然有很多方法可以回答(比如調個監視器重播。)其中一個很拐彎抹角的方法就是找一個人計算甲所走過的路徑,再除以 2π ; 對於不明究理被找來計算的人而言,他就是在做一個複雜的積分計算,但我們旁觀者知道它有一個明確的意義:答案是圈數,是一個整數!陳數可以理解成在一個比較抽象的空間中計算定義的「繞數」。透過這個譬喻也可以理解,陳數是一個跟「拓樸」相關的數,跟你庭院中有沒有噴水池有絕對的關係,但跟你走動的細節關係不大。
從這個觀點來看,出現一系列整數的序列似乎是有跡可循的,然而,這並不是故事的尾聲。1982 年崔琦的團隊首先發現上面的比值可以是 1/3、2/5等分數,這是分數霍爾效應的開端,掀起的波瀾直至今日都未能平復。
參考資料:
1. J. K. Jain, Composite Fermions.
2.M. Z. Hasan and C. L. Kane, Rev. Mod. Phys. 82. 3045 (2010).
--
[註1]但是蘭道階不足以解釋實驗中發現的平臺結構,也無法說明這個狀態的堅韌性。R. Laughlin 在實驗結果出來後不久利用材料中的雜質與無序以及電磁學中的對稱性提出了解釋,不過那部分比較抽象,就不詳談。
[註2]作者看到一些評論指出單純蘭道階不足以完整說明整數量子霍爾效應。這個評論是對的,這也是作者需要在註腳引述 Laughlin 文章的原因。
--
作者:蕭維翰,臺大物理系畢業後逃到芝加哥,吹風吹雪之餘,做研究讀博士班。可惜離開臺灣後無海可看,只能在密西根湖旁揀一方堤岸,偽裝成看海的人。科教中心特約寫手,從事科普文章寫作。
