【數學奧妙】用統計方法來分析文章的用字頻率

■巴塞隆納的數學家證實可以用一個相當簡單的數學公式來描述文章中字詞出現的頻率。

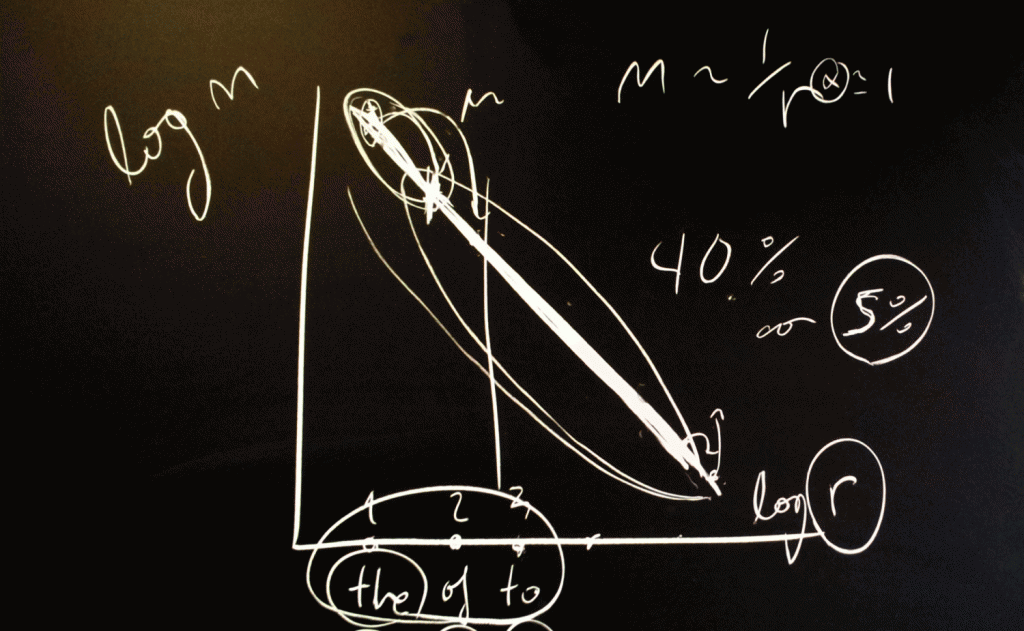
撰文｜陳勁豪

1949年，哈佛大學的語言學家 George Kingsley Zipf 提出一個經驗公式。在一個相當大的語言資料庫中，例如一本書，出現頻率最高的詞彙，它所出現的頻率大約是出現頻率排名第二的詞彙的兩倍，是排名第三的詞彙的三倍，其餘則依此類推。用數學形式來描述的話，P(n) 正比於 1/n。而且更重要的，這個簡單的數學式子只有一個參數。

這個公式相當簡單易懂，但是這個經驗公式卻一直被人懷疑其正確性，因為這個經驗公式一直沒有被仔細的用統計方法驗證過，也沒有被應用在大量的文字資料庫中來驗證其正確性。這幾點都不難想像，因為過去沒有電腦，隨便從書架上抽出一本數萬字的小說，光是整理數據就可以累死研究人員(更正確的說，是他們的助理)，所以不難想像驗證這個公式的困難度。

三位巴塞隆納大學的數學家決定來驗證這個公式。他們選中的資料庫是古騰堡計畫(Project Gutenberg)中的英文書籍。古騰堡計畫於1971年成立，有計劃的把屬於公共版權的書籍進行數位化，以達到廣泛保存各類文獻與便利流通的目的。當這些書籍被數位化之後，便可以讓電腦來協助分析這些大量的資料。這次的研究用了約三萬本作品，遠遠超過過去類似研究所用的書籍數量，同時也可以大幅提高數據分析的正確性。

分析的結果發現大概有 40% 的書籍的詞彙分佈方式依照 Zipf 公式。更令人驚訝的是，如果把整本書中只出現一次或兩次的這種罕用字去除，那麼符合 Zipf 公式的書籍數量數會大幅提高到 55%，也就是超過一半的書籍符合這個分佈。這個公式的應用範圍相當廣泛，可以從數百字的小文章到長達數百萬字的長篇巨作。從數學上來看，更廣義的 Zipf 公式應該把 1/n 寫成 1/an 的形式，但是這個研究也發現，基本上這個多出來的參數非常接近1，換句話說，1/n 是個非常好的近似。

對統計分析來說，最常見的分佈應該是所謂的常態分佈曲線，或是高斯曲線。這個分佈需要兩個參數來描述數據的分佈情形：平均值與寬度。但是這個 Zipf 卻只要一個參數就可以簡單描繪這個分佈，是相當特別的情形。

長久以來，人們總是認為文章是人類智慧的結晶。但是不論是偉大如莎士比亞或是平庸默默無聞的作品，這些作品的用字頻率卻可以用一個相當簡單的數學公式來解釋，這也是數學美妙的地方。

原始論文：Large-Scale Analysis of Zipf's Law in English Texts
相關報導：Surprising mathematical law tested on Project Gutenberg texts

--
作者：陳勁豪　科教中心特約寫手，從事科普文章寫作。2011年於美國紐約州立石溪大學(SUNY at Stony Brook)取得博士學位，研究主題為相對論性重離子碰撞(Relativistic Heavy Ion Collision)。長期擔任中文科學新聞網站「科景」(Sciscape.org)總編輯。