切比薩的新方法

■兩位數學家告訴我們，比薩不是只能切成簡單的扇形，其實還有更特別的各種切法。

撰文｜陳勁豪

當我們在家看電影、看球賽，或是開派對，甚至就是單純不想煮飯時，我們可能會直接拿起電話訂外送比薩。基本上比薩上桌的時候，都是切成扇形(而且當然是有大有小...)。這對我們來說是個習以為常的事，但對數學家來說，這並不只是填飽肚子的問題而已，而是一個特別的數學問題。

切比薩最重要的是公平，大家都希望拿到的每一片都一樣大。從最簡單的情形開始，就是比薩店的切法：每一刀都經過圓心，每片的圓心角的角度都一樣，我們自然會得到每片都是大小一樣的扇形。但是除了扇形之外，我們可以用其他形狀來填滿整個圓形區域嗎？

英國University of Liverpool的兩位數學家，Joel Haddley與Stephen Worsley，發表了一篇論文，告訴大家另外一種切比薩的方法。事實上，他們的論文討論的是另外一個更基本的問題：如何用同一個固定形狀與大小的區域(或稱為磁磚)來填滿整個圓形，在數學上稱為「曲線切割(monohedral disc tiling)」。

過去的數學家對這個問題提出一個解決的方法。可以把一個圓分成十二個全等的小塊。每一小塊各有三個邊。這種切法會得到六片帶著比薩邊的小片，另外六片則是位在比薩內部，完全不帶邊的小片。

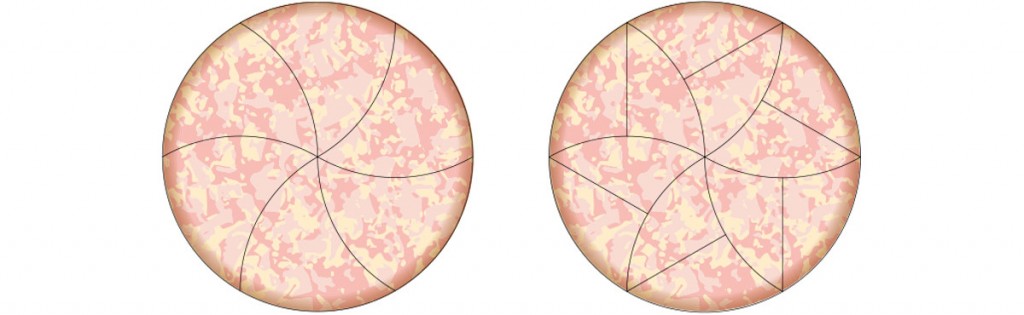
在這篇Haddley跟Worsley所寫的新論文中，他們提出了一個新的切法。他們證明他們可以把圓形用任意奇數個邊的磁磚來填滿，例如三個邊，五個邊，七個邊的磁磚...接著再把這個磁磚分成兩半，便可以分出兩片一片帶邊，一片不帶邊的「比薩」。除此之外，他們還提出了更複雜的切法，讓切出來的比薩帶有更多的形狀。

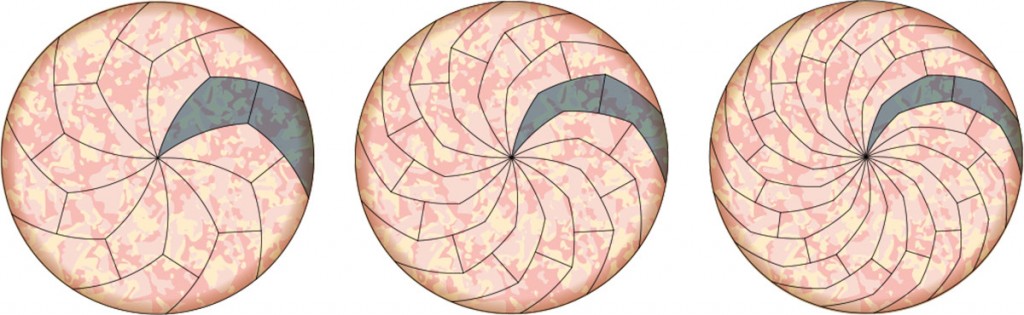
不過大家自然會好奇，這些切法真的可以拿來實際生活中切比薩嗎？他們承認，如果邊數太多，那這種切法大概很難在現實生活中重現。不過為了證明他們的作法是可行的，他們的確是把一個比薩用他們論文中提到的方法切出十二片全等的比薩小片。

我個人認為，這個新的方法不但可以應用在比薩上，甚至可以推廣到切鬆餅，切生日蛋糕等各式大型圓形的食物上。有興趣試試新切法的人，下次外帶比薩的時候記得先提醒店家不要切，讓大家在家裡試試看。

原始論文："Infinite families of monohedral disk tilings" Joel Haddley, Stephen Worsley

相關報導：
1. New Scientist 2016/01/08: Mathematicians invent new way to slice pizza into exotic shapes
2. Popular Science 2016/01/08: Cut A Better Slice Of Pizza With Math
3. Phys.org 2016/01/09: Researchers try mathematical recipe for slicing pizza

--
作者：陳勁豪　科教中心特約寫手，從事科普文章寫作。2011年於美國紐約州立石溪大學(SUNY at Stony Brook)取得博士學位，研究主題為相對論性重離子碰撞(Relativistic Heavy Ion Collision)。長期擔任中文科學新聞網站「科景」(Sciscape.org)總編輯。