【數學概念】To Be Continuous

撰文｜吳如峰

事實上，我必須先說，「連續」其實是一個很潮的概念。

我在高中的時候曾想過這麼一個問題：在我們的生活中有什麼東西是真正「連續」的嗎？在紙上畫一條線是「連續」的嗎？你覺得呢？

但其實我這樣的問題是很弔詭的！我壓根都沒有告訴你「何謂連續」！

在數學上，我們對「連續」是有一個嚴格的定義的。在剛開始學到「連續」的嚴格定義是在大一微積分課時，那時候我們說一個把實數送到實數的函數在某一個點是連續的(continuous)若且為若在那一點的附近可以找到一個小小的區間(interval)，使得在這個區間內每一點的函數值都在這一點的函數值的某個小小的區間內。

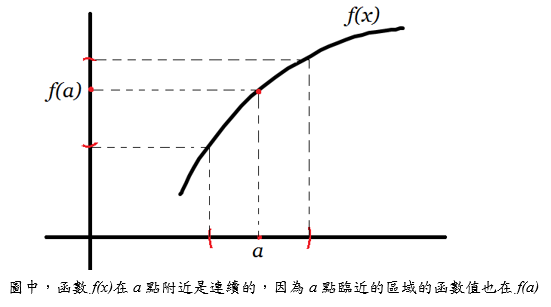藉著這個定義，數學分析[注1](Analysis)得以以一種嚴謹的姿態分析各式各樣的函數。不過，「連續」的這個概念後來被拓樸學家做了更一般化的定義：如果有一個存在兩個拓樸空間[注2](Topological space)的映射，這個映射在某一點連續若且為若存在這個點附近的某個小小鄰近的區域(neighborhood)，使得在這個區域的函數值落在這個點的函數值附近的某個小區域內。

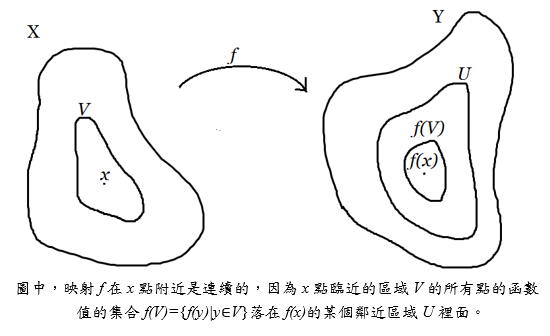其實簡單來說，「連續」是一個很直觀的概念。它的意思就是說：假如你在某一點附近的觀測值跟你的預測值相去不遠的話，那就稱那一點為連續。舉例來說：當我們今天看著地面天氣圖預測幾個小時之後的天氣時，你會發現你的預測跟實際上的天氣情況相去不遠。但有趣的是，如果我們預測幾天之後的天氣卻可能發現我們所預測的與實際上的差距極大？為什麼呢？因為，「連續」只給了我們在鄰近區域（每一個neighborhood）的資訊，卻沒有告訴我們在離我們觀測點很遠的地方會發生什麼事！

此外，「連續」也給了我們一個非常有趣的性質：中間值定理。假設溫度的分佈是處處連續的（直觀上他就是處處連續的），那麼當我們從的山下要爬到的山上時，你會發現你一定會經過一個地方的溫度是；事實上，你會經過所有到中間的所有溫度。雖然你可能會覺得很直觀，但如果溫度的分佈在某一點x不連續的話，那麼在半山腰的x處，溫度從跳到，那麼，你就不會感受到的空氣了。

現在，我想我們對「連續」有足夠多的了解了，因此讓我們回到我們剛剛所關心的問題：在紙上畫一條線是連續的嗎？

當時，我想到的答案令當時的我感到非常震驚且興奮。試想，當我們在紙上畫一條線時，紙的凹凸不平導致會導致筆跡只處於比較凸的部分，因此那條線是斷斷續續的。那紙呢？筆跡不連續，那紙總該連續吧？我想也不。想想每一顆原子都是由原子核及原子核外層環繞著的電子所構成的，而當兩顆原子擺在一起時，外層的電子會互相排斥，也因此是離散的。就連量子理論告訴我們電子的軌跡是不連續的！

不連續！我們的生活其實充斥著不連續！於是，當我們的生活是如此不連續時，「連續」實在是一個很潮的概念！

但這就衍生出另一個問題：這世界上還有真正「連續」的東西嗎？我想答案還是肯定的，就讓我們 to be continued吧！

注解：
[1]「分析」是一個數學領域，主要研究函數的各種性質。
[2]在此不多談什麼是拓樸空間，可以直接想像上次我們提到的幾何物件。事實上，還有更奇怪的拓樸空間，如果有機會我們或做更進一步的介紹。