【數學動腦】馬克杯跟甜甜圈一不一樣？

撰文｜吳如峰

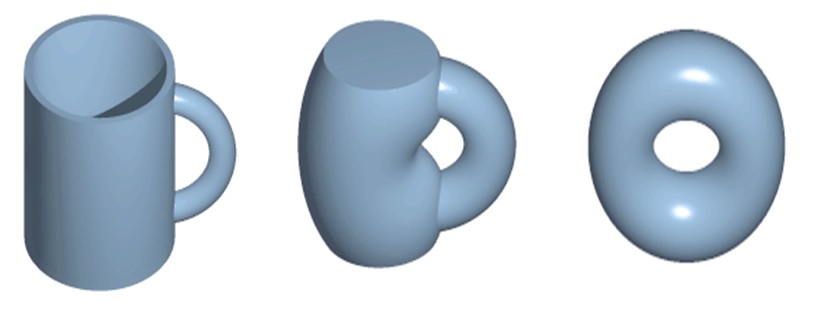
常常會有人嘲笑拓樸學家說他們分不清楚馬克杯跟甜甜圈。這是怎麼回事呢？拓樸學家為什麼會搞不清楚這兩者的差異呢？

在講解上面這件事之前就先讓我們來看一些幾何吧。其實在過去，數學家們關心過這樣一個問題：一個平面挖掉一個洞跟一個平面是否一樣？

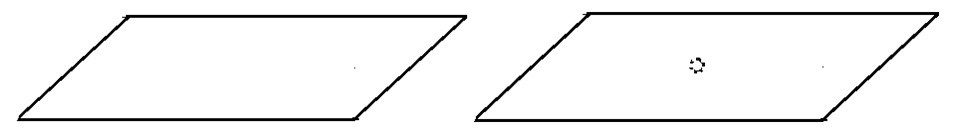遇到這樣一個幾何問題，最先想到在幾何中要說兩個幾何物件[1]是一樣的，應該是在國中時我們學過的三角形的全等性質。但三角形的全等性質該怎麼回答我們的問題呢？平面是沒有邊的啊！要怎麼使用這些全等性質呢？答案當然是不能用這樣來考慮兩個幾何物件一不一樣，因為這樣的限制太多了。

但其實在數學當中要說明兩個集合是一樣的其實很簡單，只要你可以告訴數學家這兩個集合中的元素是一對一對應，且每個元素都可以找到另一個集合上的對應元素，那就稱這兩個集合為一樣。譬如說：跟就存有這樣的關係（我可以把1對到4、2對到5、3對到6）。在數學中，我們稱對應關係為一個映射（map），而這樣特殊的映射稱為對射（bijection）。

可是數學中不單單只有沒有規則的集合（如果只是說“集合”的話，是可以很沒有規則的。你可以把任意的東西放在一個大括弧裡，就是一個集合，譬如說｛q gn ud 37 8 po @ % *｝），數學家更感興趣是具有某些結構的集合，譬如說每一個幾何物件就可以看成一個集合，而在這些幾何物件中，數學家們也會希望要說「兩個幾何物件相同」的映射必須具有某些特別的性質，於是便要求了「連續」這個條件。（此處的連續是所謂的連續函數的一般化，在此並不多提它的定義，只需要有一些直觀即可。）當一個對射是雙向連續的時候，我們就稱它為同胚(homeomorphism)。因此，數學家們視兩個幾何物件是否一樣取決於這兩個幾何物件中是否存在一個同胚，於是這樣的概念就成了拓樸學的濫觴。

現在就讓我們想想最一開始的兩個幾何物件（平面及平面挖掉一個洞）是否可以造出一個同胚使它們一樣？又或者，你可以回答出永遠不可能存在著這樣的同胚？你會發現：要回答這樣的問題其實非常非常困難，因為你的直覺告訴你它們是不一樣的，所以你必須試著說明不存在這樣的同胚，但你要怎麼說永遠找不到這樣的同胚呢？數學家們也為此感到困擾。

後來，數學家們發現，每一個幾何物件都有一些它本身不會變的性質，稱為不變量(invariant)。什麼意思呢？就像是每一個人的生日是不會變的，因此如果有兩個人的生日不同，他們就不會是同一個人；同樣的，如果可以發現兩個幾何物件的某個不變量是不一樣的，那它們就不會是同胚。（注意：同樣的不變量並不代表兩個幾何物件同胚，就像相同生日的人不一定是同一個人。再者，一個集合可以有很多不變量，就像身分證字號、父母、兄弟姊妹都可以是人的不變量一樣。）

於是，這樣的想法指引我們去發現這兩個幾何物件的不一樣的不變量。那有什麼可以當成不變量呢？說穿了，「幾個洞（虧格(genus)）[2]」就是一種不變量。因此，平面的這個不變量是0、而平面挖掉一個洞的這個不變量是1，因為0不等於1，所以平面跟平面挖掉一個洞是不一樣的。

現在，讓我們回到甜甜圈跟馬克杯。你會發現，這兩個在三維空間中的物體都是只有一個洞！並且，因為他們在數學中也滿足其他條件（緊緻、連通且可定向性），所以在他們中間存在著一個同胚！當然，也為此在這樣的觀點下，他們被視為一樣。

於是我們解決了我們的問題，但故事並沒有因此結束。數學家們因為這種把幾何物件轉換成觀察不變量的這個方法而逐漸發展出如今的代數拓樸。更一般化一點，我們也可以不僅僅侷限在幾何物件上，你也可以在一般集合、甚至在生活中發現這樣的把戲被廣泛地運用。然後你會發現：原來再簡單不過的事情也可以很數學！

註解：
[1]幾何物件泛指各類以幾合觀點來探討的物件，例如：一個圓、一個球、一個甜甜圈……等
[2]如果兩個幾何物件都是緊緻(compact)、連通(connected)且可定向性(orientable)，那虧格數量就會決定他們是否同胚。意思是說，如果兩個幾何物件都是緊緻、連通且可定向性，並且虧格數都一樣，那他們就會同胚。（在此並不多提緊緻、連通、可定向性這三個性質，若以後有機會的話會介紹）。