【大宇宙小故事】24 後繼有人

撰文｜葉李華

高斯笑了！

高斯很久沒有這樣笑了，尤其是在晚年，他的個性越來越古怪，笑容也就越來越少。

這天他卻笑得很開懷，因為他聽了一場精采的演說，確定自己後繼有人。

時間是公元1854年6月10日(距離高斯辭世只有八個月多)，地點是哥廷根大學數學系。講者是高斯的得意門生黎曼(1826-1866)，三年前，他在高斯指導下完成了博士論文。

今天的演說和博士學位無關，而是黎曼希望成為高斯的同事。為了證明自己勝任這份教職，他必須依照慣例，做一場有專業水準的公開演說。

半年前，黎曼提交了三個題目請恩師勾選。不知是不是故意的，這三個題目的難易程度有著明顯的差別。

第一個題目和黎曼的博士論文有些關聯，沒有太大的挑戰性；第二個題目是關於二元二次方程式，當然更不值得一提；第三個題目＜論幾何學基礎之相關假說＞則讓高斯眼睛為之一亮。

可想而知，第三個題目脫穎而出，而黎曼的表現甚至超出了高斯的預期。

●十九世紀的愛因斯坦

在數學史上，這場演說具有承先啟後的重要地位。它為微分幾何學指出一個明確的新方向──以N維流形為研究對象的黎曼(微分)幾何。

弔詭的是，這篇遲至1868年才正式發表的講稿，可以說是出了名的難懂。

原因之一，為了顧及聽眾中還有其他領域的學者，黎曼無法以數學家的語言暢所欲言。

(但這絕不代表數學不好的人也能看懂這篇講稿。)

原因之二，由於演說時間有限，黎曼將內容盡量濃縮，幾乎到了濃得化不開的程度。

(如果他詳細闡述，至少能再寫出一篇博士論文。)

原因之三，這個主題和非歐幾何關係密切，黎曼卻採取明哲保身的態度，從頭到尾欲言又止。後世學者只能從字裡行間推敲他的原創性倡議──以微分幾何作為研究非歐幾何的利器。

(不久之後，果然有數學家響應這個號召，而且成果豐碩。)

原因之四，這篇講稿有四分之一的內容與物理學有關，更明確地說，是在探討(微分)幾何和物理的密切關係。

(因此有學者認為，若非黎曼英年早逝，廣義相對論很可能提早五十年誕生。)

●二十世紀的黎曼

幸好有愛因斯坦，在二十世紀初繼承了黎曼的未竟之志。

其實就學術傳承而言，愛因斯坦並未直接受到黎曼或高斯的影響。在發展廣義相對論的過程中，愛氏赫然發現相關的數學工具(微分幾何與張量分析)早已由三位數學家(Bianchi, Ricci, Levi-Civita)為他準備好了。

那三位數學家都是義大利人，這點並非巧合，而是因為黎曼和義大利有深厚的淵源(他曾數度造訪這個國家，傳播他的微分幾何福音)。因此，愛因斯坦可以說是間接受到黎曼的影響，正如同廣義相對論是以間接的方式(經由微分幾何)引進非歐幾何。

如上所述，黎曼在1854年那場演說中對非歐幾何欲言又止，但後世學者從字裡行間讀到一項真知灼見：不同的彎曲空間很可能藏有不同的非歐幾何。由於彎曲的空間和時間是廣義相對論的中心思想，由此可知在這個理論中少不了非歐幾何的身影。

廣義相對論所探討的彎曲空間通常很複雜，例如黑洞或蛀孔，然而「宇宙的三維結構」卻是例外。這並非物極必反，而是當我們在研究宇宙結構的時候，通常只關心大略的形狀，不會斤斤計較細節。正如同地球表面有高有低，還有一點啤酒肚，但在許多實際問題中，我們還是能將它視為完美的球形，不會有太大誤差。

●宇宙是什麼形狀

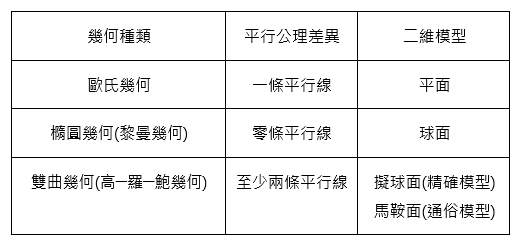
答案只有三種可能，其中之一是三維的歐氏空間，另外兩種則是非歐空間。而在這三種可能中，只有第一種容易想像，因為歐氏幾何正是根據人類的直覺發展出來的。另外兩種非歐空間就比較難懂，所以我們最好從頭說起。

在上述那場演說中，黎曼用言外之意的隱晦方式指出：高斯等人所發展的(二維)非歐幾何──如今所謂的雙曲幾何，其特點是平行線超過一條──或許能用一種特殊的曲面來實現。至於另一種(二維)非歐幾何──如今所謂的橢圓幾何──則對應於歷史悠久的球面幾何(請參考＜同名同姓又同源＞)。

就微分幾何而言，球面就是「彎曲傾向處處相同」的曲面，正式的說法則是「球面的曲率是一個正的常數」。因此黎曼(又藉著言外之意)指出，若能找到「曲率為負常數」的曲面，應該就能具體實現另一種非歐幾何──雙曲幾何。

可惜黎曼自己一直沒機會鑽研這個問題，直到他去世後，才由深受他影響的義大利數學家貝氏(Eugenio Beltrami, 1835-1900)找出雙曲幾何的第一個具體模型，並命名為「擬球面」。

不過，「擬球面」的形狀太過古怪，因此在比較通俗的文獻中，通常都用(曲率為負但不是常數的)馬鞍面來代替。久而久之，馬鞍面便成了雙曲非歐幾何的「識別標誌」。

最後再強調一點，大家都知道二維歐氏幾何能直接推廣到三維，事實上，兩種二維非歐幾何也可以這麼推廣。但由於我們活在三維空間中，所以不可能畫出具體的圖像。

●回到原點？

總而言之，宇宙的大致形狀只有三種可能：

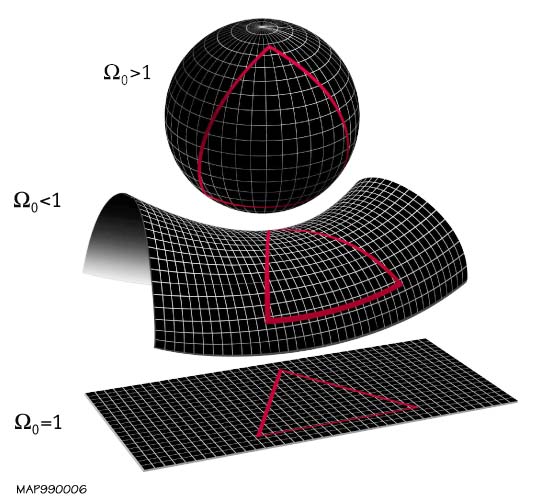
一、如果宇宙是三維歐氏空間(曲率為零)，那就完全符合人類的直覺，無須多做任何說明。

二、如果宇宙是符合雙曲幾何的三維空間(具有負曲率)，那麼正如馬鞍面可視為「有起伏的平面」，宇宙的形狀就是「有起伏的三維歐氏空間」。我們自己生活在這個空間中，無法藉由更高的維度看到那些起伏，但至少能遵循當年高斯和羅氏的想法，根據光線的路徑來確定這一點(請參考＜歐幾里得與世界大戰＞)。

三、相較之下，符合橢圓幾何(具有正曲率)的三維空間最難想像，因為它和球面一樣，是一種「有限卻無邊界」的幾何形體。

還好我們能用球面來類比一番，比方說，如果你是球面世界的二維生物，站在北極朝四面八方極目眺望，那麼只要你視力夠好，你的「視野」就會以赤道為分水嶺，從逐漸擴大變成逐漸縮小，最後甚至會縮成一個點，也就是那個球面的南極，亦即距離北極最遠的地方。

然後，如果你讓視線繼續延伸，就一定有機會看到自己的後腦勺。(球面世界是二維空間，其中的光線跑不出去，所以只能沿著球面繞圈圈，最後回到原點。)

只要將這個例子加高一維，我們便能得到如下推論：你站在地球上，朝著上下四方極目眺望，只要你視力夠好，你的視野就會以「太空中某個球面」為分水嶺，從逐漸擴大變成逐漸縮小，最後甚至會縮成一個點，該點就是宇宙中距離地球最遠的位置。

然後，如果你讓視線繼續延伸，就一定有機會看到自己的後腦。不過根據廣義相對論，你要一直等到地老天荒。

看到這裡，想必大家急著想知道宇宙到底是哪一種形狀。但是建議大家先想想，這三個答案哪個最不可能？

就機率而言，最不可能的當然是歐氏空間。正如同根據正負號將實數分成三大類，其中最不可能被抽中的當然是「零」這一類。

可是信不信由你，根據目前最新的觀測結果，歐氏空間竟然是呼聲極高的候選者。甚至早已有科學家從理論出發，試圖對「歐氏宇宙」做出合理的解釋。

至於真相如何，且讓我們拭目以待。然而，如果歐氏宇宙真的脫穎而出，黎曼與愛因斯坦也絕非走了一大圈又回到原點。