【電腦與數學】俄羅斯方塊實在有夠難!?
■ 俄羅斯方塊看起來只是一堆不停掉下來的磚塊,但就電腦科學的意義上,卻是遠比數獨要困難的真正「益智遊戲」。對於涉及時間而且可能沒有最佳解答的問題,人類做得不見得會比電腦差。

撰文 ∣ 張譽鐘
自從1984年蘇俄科學院的Alexey Pajitnov創造了俄羅斯方塊後,幾乎所有運用到電子計算機的設備都有它的影子:手機、遊戲機、電子詞典,甚至有好事者藉由控制大樓每間房裡的燈光來遊玩。二十多年來俄羅斯方塊的根本結構並沒有什麼太大的改變—-共七種面積相同的方塊隨機的從上端掉落,而玩家就是要在有限的時間裡將這一系列的方塊堆疊並盡可能的填滿每一列方塊堆。
但,你有沒有想過,俄羅斯方塊有多難呢? 聰明的你也許想了一會兒就發覺,還有一個更根本的問題:「怎麼樣定義困難與否呢?」
在計算機科學裡,一個問題的困難度由解決它所需的時間而定,當然,我們在這裡所談論的是可以被解答的問題,像是「103是不是質數?」之類存在解答的問題,而困擾計算機學家已久的問題之一,便是「NP問題」,亦即「未確定能否在多項式表列的時間維度裡解決的問題」,而多項式便是像是5X3+4X2+2X之類的式子,而變數X可以被視為我們輸入的資料量。也許你會問,即使像上述的式子,我們代入X=100,就已經是5040200這種數字了,為何要以「多項式時間」做為標準呢?
理由其實非常的簡單,我們看看比較的圖解就知道了——因為多項式時間還只是小兒科而已!!還有像是「2X」這種指數時間的怪獸存在,所以我們說NP問題可能是極為困難的,因為我們不太可能找到多項式時間的解法!
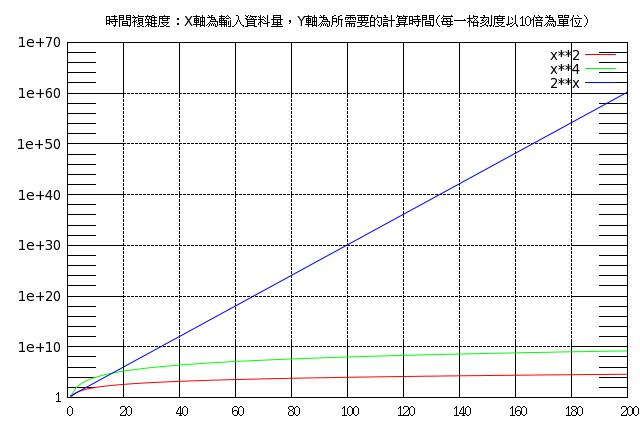
現在我們回到俄羅斯方塊上,也許你已經猜到,俄羅斯方塊已被證明是一個NP問題(而且還是NP問題裡特別難的NP-Complete問題),並且證明的科學家還是以較簡單的版本-—所有掉落方塊的先後順序皆已得知的狀況下求證的,所以實際上娛樂用的版本只有可能更難而已!
不過,科學家的目標是極大化消去的列,而人類在遊玩的時候,並不是依照此一標準進行的。我們倚靠啟發式的演算法(Heuristic Algorithm),也就是說,我們尋求的並非最佳解。而也許就是因為這一點,所以人們會持續的玩下去(因為沒有必勝的玩法)。
另外一點值得注意的是時間性。許多遊戲都有時間的限制,俄羅斯方塊也不例外,玩家要不斷地抵抗時間壓力,盡可能避免遊戲結束。試想,若你可以玩一個無限慢的俄羅斯方塊遊戲,甚至可以拿紙筆或者另外跑個程式來運算下一步怎麼做才「最正確」,那麼想必應該很無聊吧?
並非所有廣受歡迎的遊戲都是困難的,像是數獨就不是。張海潮教授在《說數》一書中曾經提到,數獨這種東西,在數學的意義上對於人類的智慧沒有貢獻,充其量是打發時間用的。也許這有點令人意外,幾年前大街小巷那些埋首報紙、甚至熱衷到購買專門出版品的人們花費那麼多時間的遊戲,與區區的俄羅斯方塊相比,竟然是相對簡單的?
?
延伸閱讀:Tetris is Hard, Made Easy(Ron Breukelaar, Hendrik Jan Hoogeboom, and Walter A. Kosters from Universiteit Leiden 荷蘭萊頓大學電腦科學研究中心論文)
責任編輯:MissZoe
分享到facebook

大腦在處理某些複雜問題型態的直覺應該不是計算機處理的模式吧。我對你說的NP難度有些不了。
對啊~這樣講是沒錯~
這篇文章中「難」的定義是指「對電腦很困難」。
電腦沒法幫人類玩俄羅斯方塊,但可以輕鬆解開複雜的數獨。在這個意義上數獨並不「難」,它可能很花人類的時間,但不花電腦的時間。所以張海潮教授才會說數獨其實不「困難」,不應該花腦力去做,給電腦跑就好.....(在他的《說數》p46-49提到)
不過最近科學家發現絕大部分歷久彌新的小遊戲像「倉庫番」、「踩地雷」跟「填色問題」都已證明是NP問題,所以我猜想人類可能不由自主的就會對某種意義上「困難」的東西保持高度的興趣....
(我是原作...請大家鞭小力一點)
http://www.wired.com/gamelife/2009/09/how-tetris-changes-your-brain/
剛好看到一則有趣的報導:俄羅斯方塊改變你的腦(變聰明)
但...這研究是俄羅斯方塊公司贊助的!(有點微妙?XD)