【探索22-4】問風雨雷霆之故

早在兩千多年前，莊子就曾經留下「問天地所以不墜不陷，風雨雷霆之故」一辭，可見天氣是自古以來為人們所關心的課題；這份關心到今天或許還要有增無減，舉凡工作、聚會、旅行，甚至是穿著打扮都會參考氣象預報提供的資訊；人們也不時為氣象天候而感動好奇。郭鴻基教授從科學研究的本質出發，從氣象學的歷史中觀察研究思維如何演替，進而探看在當代，大幅躍進的計算機能力如何協助氣象學家更精確的掌握天氣。

講者｜臺灣大學大氣科學系教授 郭鴻基
彙整撰文｜蘇建翰

●科學研究如同瞎子摸象

在東方認知論裡，很早就開始思考知識的侷限性，比如莊子提過「井蛙不可以語於海者，拘於虛也；夏蟲不可以語於冰者，篤于時也」，井蛙之於海是空間上的限制，夏蟲之於冰則囿於時間上的區隔，一個人所能看見並加以思考的面向，其實是受其出身的時空背景限制的；另外，「吾生也有涯，吾知也無涯，以有涯逐無涯，殆矣」則更清楚的點出一個人用盡一生也無法習得這世界上的所有真理，科學研究往往只能透過有限時空之觀察資料試圖推導能用來描述無限時空的法則。

 

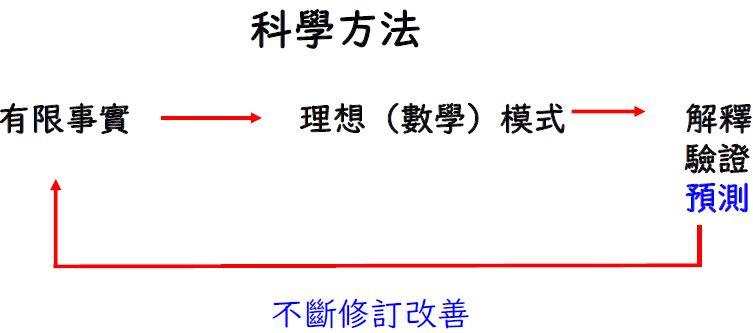
科學研究的進行，或許可以比擬成瞎子摸象的過程，即使是同一隻大象，也會因為使用的感官不同、接觸的部位不同，而得到不盡相同的結論。這些不同方式「摸」來的結論，必須能夠經得起檢驗，才能成為「事實(Fact)」，而非流於個人的「意見(Opinion)」。經過長時間的摸索，西方科學發展出一個系統性的、可靠的科學方法，奠基於邏輯，在有限的事實之上，提出假說並進行驗證與預報，然後不停地修訂改善，長期下來我們就能得到更可靠的知識。

在東方我們常說「學而不思則罔，思而不學則殆」，而在西方則將學思整合在科學寫作內，並發展出一套方法論：從定義問題開始，從而設計、執行實驗，接著檢驗與解釋結果，最後進行完整立論並連結外部研究。寫作就是最高階的思考，透過科學寫作的過程，可以梳理自己對問題理解的足與不足之處，以寫作來完善科學探就。

●數量讓知識清晰——氣象背後的數學思維

在早期，人們普遍相信子代的特性是由雙親混和而來，這個信念其實只要透過簡單的數學列式，就會察覺蹊蹺之處，因為假使該說法為真，長此以往後代的特性會趨向單一，明顯與實際情況有所出入。從這個例子可以說明，要研究一個問題，在善用科學方法、科學寫作方法論等工具幫助思考以外，主要我們還需要和該問題相關的數學工具，或者說是數學思維，數學思維可以幫助我們提出問題，有量化的數字，知識也會更清晰。

在許多的科學領域，該學科的歷史其實就是由一連串量化數字所書寫出來的，這在氣象學上也不例外。彩虹如何的絢彩斑斕、朵朵白雲如何讓人自在、颱風來臨又是如何讓人繃緊神經，這些都是大眾在面對不同天氣時容易有的感受，不過在當代的氣象實驗室裡，各種天氣現象並非由感受組成，而是用數字來呈現的。

成功估算彗星回歸週期的哈雷(Edmond Halley, 1656-1742)曾經提出一個大哉問：「天文學可以預測76年的尺度，為何氣象不行？」要回答這個問題就必須要知道天氣究竟是由線性還是非線性控制方程式來描述。線性方程式可以想像由加減符號組成，通常變化較平緩，非線性系統則常由乘除號組成，變化的幅度、頻率通常較為劇烈，涉及跨尺度的交互作用。天氣之所以難以預料，在於其背後的控制方程式主要由非線性系統組成。

●計算機的加入促進氣象學往實驗科學的轉向

 

理查森(Lewis Fry Richardson, 1881-1953)是一位擁護和平主義的英國科學家，在其一戰期間擔任救護車駕駛員的兩年，閒暇時專注在計算氣象相關的非線性方程式，試圖進行氣象預測。後來，因為氣象預報幫助毒氣施放，使其深惡痛絕而不再進行相關的工作，也留下一個未竟的夢想：理查森希望能建立一個預報組織，將全球切分成六萬四千格網格，每一個網格分配一位計算員進行方程式的運算，從而達到全球氣象即時預報的目標，這可以說是平行處理想法的先驅。

以當時的時空背景來看，這想法是相當天馬行空的，需要大量的人力進行大量的運算，才能得到短時間內的天氣預報，而且當時對氣象控制方程式理解亦不足、觀測之不足以及誤差還可能相當巨大。到了現代，氣象科學之了解加上有電腦的協助，我們可以說已經代替理查森完成他的夢想。ENIAC (Electronic Numerical Integrator and Computer)作為史上第一部通用電腦，即被投入氣象預報的工作，隨著科技的進步、計算能力大幅的提升，當電腦預報的結果逐漸超過預報員的經驗時，也標誌著氣象學往數值模擬、實驗科學的轉向，不再只是過往單純以氣象圖判讀為主的經驗科學，氣象數學模式是科學家的實驗室。

●數值模擬的挑戰與氣象學的未來

想要盡可能準確的計算氣象背後的非線性系統，就需要面對幾個數值模擬的挑戰，比如一個系統中會有許多不同尺度的交互作用，不僅在影響的空間尺度上不同、在產生的影響數量級上不同，影響的時間長度也不同，然而在數值模擬中我們常常需要忽略乍看似乎微不足道的因子，這就導致模擬的誤差產生，在非線性系統中，並不是規模小就可以不考慮，小尺度之擾動亦可成長成較大尺度的系統，像是熱帶平靜無風的地區之小擾動可以漸漸形成颱風，對台灣人來說即是非常熟悉的天氣現象，這類無中生有的例子也是所在多有的。

 

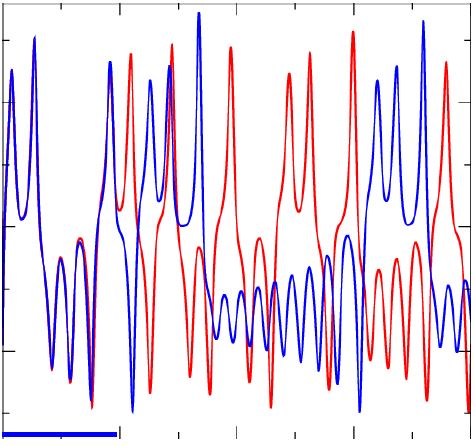
由美國科學家勞倫茲(Edward Norton Lorenz, 1917-2008)所發現、提出的渾沌理論即說明在一個非線性系統中，即使該系統是決定性的，初始參數的微小差異都能產生隨機性的結果，差異可能相當巨大。勞倫茲的發現解釋了為什麼我們幾乎無法找到相同的兩片雪花，因為每片雪花生成的環境即使相鄰也都有所差異，也說明我們耳熟能詳的「蝴蝶效應」：「一隻蝴蝶在巴西輕拍翅膀，可以導致一個月後德克薩斯州的一場龍捲風。」因此，由於非線性系統可以由大而小、有小而大的特性，民眾日常最關心的天氣可預報度也就有其限制，隨著預報的日數拉長，誤差也就越大，如何盡可能提升預報的準確度，仍是現代氣象學的挑戰，但決定性預報有其極限。

在數值模擬的協助下，現在我們認識到了許多氣象系統的交互作用如何發生，比如郭鴻基教授研究主題之一的渦漩所產生的細絲帶，即牽涉到不同尺度交互作用，一如攪拌咖啡杯中奶精所產生的細絲帶會改變互融的速率，大氣中大小渦漩產生的細絲帶也會改變物理、化學的反應，產生不同的天氣現象。在氣象科學有所進展的同時，也有更多的問題等待被釐清，例如近四十年來氣候變遷、極端天氣即逐漸成為人們所重視的議題，此外，氣象學也能進行跨學科的交流，比如颱風造成土石流，土石流又會如何影響沿岸生態即是氣象和生物這兩門非線性系統結合的例子。

再過去，理查森需要耗費兩年專注進行氣象計算的工作，而當代的我們很幸運地能擁有電腦強大運算能力、新興人工智慧技術從旁輔助，結合過去無數科學家累積許多氣象系統背後控制方程式的相關知識，透過科學方法等合理可靠的工具來摸天氣這頭巨象，氣象科學便能持續地有所進步，可以走得更遠。

--
本文整理自：108/10/26由郭鴻基老師在臺大思亮館國際會議廳所主講之「問風雨雷霆之故」演講內容。