ν =5/2 & 7/2,分數量子霍爾態與向列相,從拓樸序到自發對稱性破壞

根據文獻 [3],在增加的壓力下,原本的量子霍爾態會先變成向列態最後變成一般的費米液體。
撰文|蕭維翰
前陣子讀者曾撰寫了一系列關於量子霍爾效應(Hall effect)的文章,其中有數篇討論了 v=5/2 的基態該是什麼:究竟是 Pfaffian, anti-Pfaffin, 還是 PH-Pfaffian,或者都不是等等。即便在理論上這個議題依舊懸而未決,這幾年的實驗進展卻沒有給理論學家喘息的空間,反之,越來越多的新發現讓分數量子霍爾效應所牽涉的物理更加豐富,也讓學者們困惑同時又嚮往。
暫時從理論抽身,今天筆者想跟大家分享最近在分數量子霍爾效應實驗上針對 v=5/2 與它的夥伴 v=7/2 的新發現 [1, 2, 3],看看他們怎麼跟所謂的向列相(nematic phase)產生關聯。
首先讓我們複習 v=5/2 或 7/2 是什麼意思。假若我們在一個二維空間中放入一堆電子,當我們施加一個垂直方向的磁場,單電子的能階會形成蘭道階。每個蘭道階就像公寓的某層樓,裡面有很多「房間」(也就是軌域),要形成一個多粒子的量子態,每個電子會被放進某層樓的某個房間。v 代表的物理意義就是被填滿的蘭道階數目。因為實際上的電子可以帶有兩個自旋,v=5/2 對應的是第一個蘭道階的兩種自旋態都被填滿,而第二個蘭道階的第一個自旋態被半填滿。同理可推,v=7/2 是將第二個蘭道階的第一個自旋態也填滿,而第二個自旋態半填滿。圖像可參考圖二。
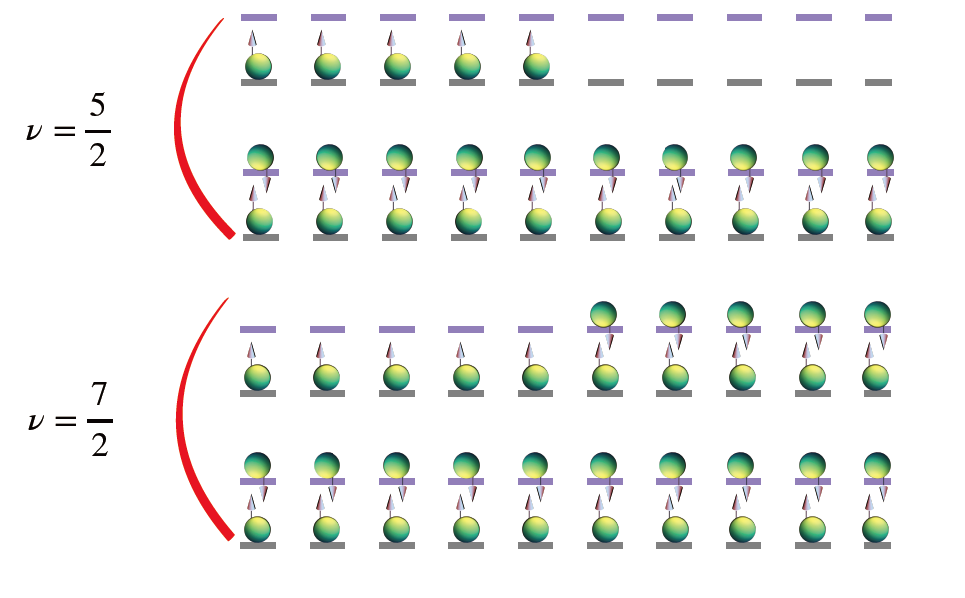
我們圖示 5/2 跟 7/2 的量子霍爾態在蘭道階中的排列情形。
半填滿的蘭道階在最初步的分析中會形成一個費米海,但實際上 v=5/2 跟 v=7/2 都是有能隙的狀態(gapped states)。我們已經說明過如何從一個沒能隙(gapless)的費米海去產生一個有能隙的狀態,使用複合費米子的語言,可以理解為複合費米子形成超導體而導致有限的能隙。讀者可以查閱之前的文章(或裡面的參考文獻)來回憶。
從實證的觀點,我們可以忘記複合費米子這些抽象名詞,總之 (1) v=5/2 (v=7/2 )是個絕緣體(因為它有能隙),(2)它是個分數量子霍爾態(Fractional Quantum Hall state, FQHS),也就是當你施加 x 方向的電場,測到的 x 方向的電阻 Rxx 為 0,而施加 y 方向的電場時,測到 y 方向的電阻 Rxy 為 0。在 Rxx = Ryy 的意義下,這個狀態是有旋轉對稱性的。
同樣從實驗的觀點,這些事情在更高的狀態 v =9/2, 11/2, 13/2 ,並不為真,意思是在這些態裡面我們都有 Rxx ≠ Ryy 。
從微觀的角度,有很多物質相可以導致 Rxx ≠ Ryy ,經由跟實驗材料的性質比對,物理學家把可能性侷限到所謂的向列相(nematic phase)。在本文剩下的段落中,我將 Rxx ≠ Ryy 與向列相視為互文。之後我們將另外花篇幅較精確地說明它的意義。
另外,今天我們只聚焦於 5/2 和 7/2。最簡單的問題(之一)是,這樣的旋轉對稱性能不能被破壞呢?當然,總是有一些直接但不那麼有趣的方法可以破壞它,譬如我們在平面的方向也施加磁場。因此,更有意義的問題是,能不能讓這個旋轉對稱性被「自發破壞」呢?
對稱性的自發破壞已經是很老的問題了。萬年不舊的例子就是磁鐵,即便我們不施加任何外加磁場,磁鐵依舊「自發地」偏好某個方向。
然而在 5/2 這樣系統中,對稱性的「自發破壞」是個有趣的議題。回憶我們在 Pfaffian 那幾篇文章的討論中,曾提及 5/2 是可以有「拓樸序」(topological order)的。在一般來說相變化(phase transition)的例子裡,我們會將拓樸相之間的變化和因為對稱破壞所產生的相變化分開討論,如當我們在討論後者時,通常就會集中精神討論順磁性(paramagnetism)跟鐵磁性(ferromagnetism)之間的變化,不會將拓樸的物理拉進來一起談。但在這個問題中,我們確有機會討論從一個拓樸相到一個對稱破壞相(symmetry broken phase)的相變化。
在 2016 年的一篇 Nature 文章中 [1],這樣的相變化終於被發現並報導了出來。該文指出,從一個5/2 的量子霍爾態(FQHS)出發,一路增加系統的壓力,當壓力超越某個閥值的時候,系統被觀測到發現一個相變化,進入到一個旋轉不對稱的狀態。實驗上所給出的證據是,它們測量不同壓力值下的Rxx 和 Ryy ,發現隨著壓力變大,測量結果一路從 Rxx = Ryy = 0 轉變成 Rxx ≠ Ryy 。
而後在 2018 年的另一篇文章中 [3],他們對 7/2 的量子霍爾態也進行了量測,並發現了類似的定性行為,並且指出要進入 7/2 所需要的壓力閥值比 5/2 要顯著地小。另外,他們提供了其他的測量,來說明壓力應該不是決定這個相變化的唯一方式(因為壓力是個巨觀的熱力學變數,改變壓力時,其實也改變一系列的微觀變數。)該文也給出一些論述,說明經過蘭道階混合與樣品的有限厚度影響後的電子交互作用在這個相變化中地位舉足輕重。
目前理論物理學家們,還不完全知道造成這樣相變化的微觀機制是什麼,其中一個可能的腳本是討論複合費米子因為某些強勢的蘭道參數而造成的相變化。我們將在之後介紹向列相時一並說明這句話精確的意涵。
參考資料:
[1] N. Samkharadze, et al, Observation of a transition from a topologically ordered to a spontaneously broken symmetry phase, Nature Physics 12, 191-195 (2016)
[2] K. A. Schreiber et al, Onset of quantum criticality in the topological-to-nematic transition in a two-dimensional electron gas at filling factor =5/2, Phys. Rev. B 96, 041107(R) (2017).
[3] K. A. Schreiber et al, Electron-electron interactions and the paired-to-nematic quantum phase transition in the second Landau level, Nature Communications (2018) 9, 2400
--
作者:蕭維翰,臺大物理系畢業後逃到芝加哥,吹風吹雪之餘,做研究讀博士班。可惜離開臺灣後無海可看,只能在密西根湖旁揀一方堤岸,偽裝成看海的人。科教中心特約寫手,從事科普文章寫作。
