路徑積分與費曼圖（下）

撰文｜蕭維翰

在前文中筆者指出，路徑積分在發明之際主要是作為另一種計算給定物理過程所對應躍遷振幅的方法，費曼圖是物理過程的圖像表示，當畫出一個費曼圖，原則上我們能夠將它拆解成一些小過程，而每個小過程可由費曼規則對應到某個數學式，也就是我們所求的答案。

在費曼的工作之前，儘管人們已經知道了在量子場論中進行這種計算的方法，但當時，這幾乎是只有最頂尖的理論物理學家才能進行的計算，而今任何一個研究所水平的物理本科生幾乎都能進行最簡單的微擾理論計算。1965 年一起與費曼分享諾貝爾物理學獎的 J. Schwinger 便曾評論道：

「一如近年來的矽晶片，費曼圖將帶給了大眾計算能力。」

除了上述在粒子物理的計算中舉足輕重，路徑積分與費曼圖的技巧也被廣泛應用在一般量子力學與統計力學的計算之中。讓我們舉一個簡單卻又實際的問題。

高中物理中，一個很重要的物理模型是彈簧的簡諧運動，到了量子力學，依舊是最基本而可解的問題之一，意思是我們清楚知道它的能階、波函數，並且能計算所有想計算的性質。從能量的角度來看，簡諧運動處在一個正比於位移平方位能之中，而被彈簧束縛的粒子便在原點附近震盪。物理學家可以問的問題就是，那如果考慮三次方位能，或四次方位能，那基本的物理圖像有什麼改變？

在做任何計算之前，大家可以先猜想，從降低總能量的觀點來看，三次方的位能不論係數正負，總有一邊是沒有底的，那麼物理態就會為了降低總能量而往那個方向滑落，也因此，這樣的模型不會有穩定的基態（ground state）。

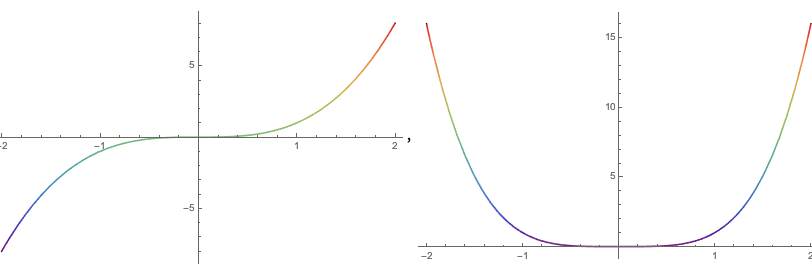
是以一般教科書在考慮推廣時，通常會注重在四次方的位能（並取其係數為正）。這樣的位能在粒子物理中也有很經典的應用，譬如最簡單的希格斯機制（Higgs mechanism）便是由考慮希格斯粒子在類似的位能中的物理效應。然而，今天我們就問一個簡單的問題——若在知道答案的平方位能上加上小小的四次方，那麼這個系統的能階會怎麼改變呢？

具體而言，所謂「小小的」意思是，我們可以用一個參數 g 作為這個四次方向的係數，在形式上我們可以讓 g 任意地小，感興趣的物理量能可以寫成沒有 g 的值加上g 一次方的修正、二次方的修正……，以此類推。（專業一些些說，就是寫成 g 的泰勒級數。）在量子力學課本中，有標準的流程，讓我們計算到所想要的 N 次方的修正。

計算四次方位能導致的 g 一次方能階修正也是個課本的標準習題，但標準課程不太提的是當我們嘗試計算高次方會發生什麼事。三十秒可以說完的答案是，你可以計算 g 平方項、三次方項、四次方項……，但當你想要把他們加起來時，答案是無限大（不收斂）。

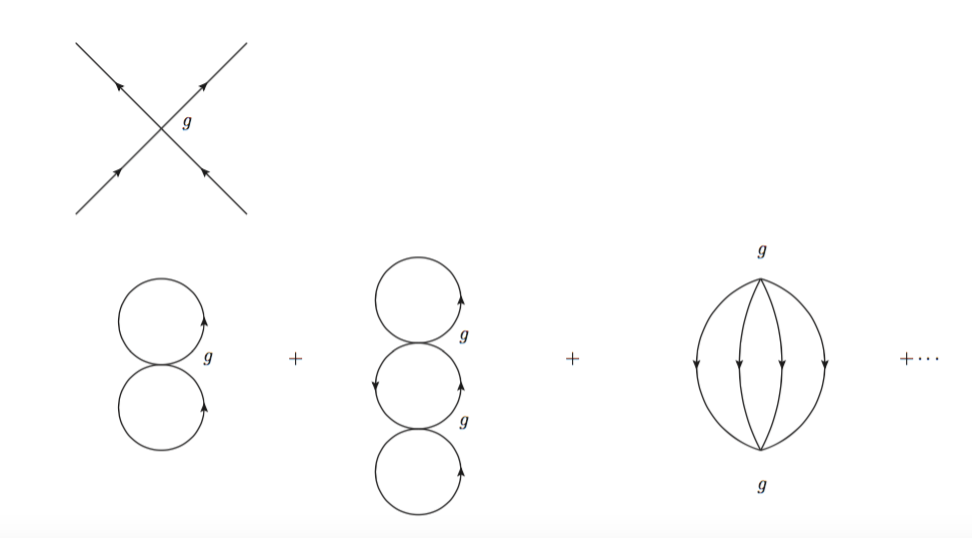
數學上有一系列技術在處理這種級數的加總，但那不是本文最感興趣的課題，筆者想指出的是，若依照標準課本教授的方法進行計算，一般人可能要計算到很高次項才會開始意識到這個答案沒辦法輕易地被加總。然而，使用路徑積分來計算這個修正時，我們可以將整個和視覺化為費曼圖，由於這是個四次方的位能，g在費曼圖中變成一個連接四條線的節點，而g 的 N 次方項的貢獻可視為所有具有 N 個節點的圖的加總。

給定某個 N，透過高中所學的排列組合可以推論出存在的費曼圖數目，因此在進行真的細節計算前，我們便可以預想在 N 極大時，每個次方會貢獻約略 N! 這麼多張的圖，N! 的無窮級數是無法收斂的，從而我們不只輕易地知道這個級數無法收斂，還知道背後的原因，與無法收斂的程度。

總結這兩篇短文，筆者想要闡明路徑積分與費曼圖除了提供在一般科普文章談論的物理理解外，也在定量的計算中提供了直觀、有效的工具。然而，筆者也必須指出至少兩點缺陷：其一，在數學上被嚴格定義的路徑積分寥寥可數，因此在可預見的未來。其二，費曼圖只定義了微擾的解。幾十年來，我們在這兩個問題上各自有進展，然而長路漫漫，完整的解答還有待未來的物理學家完備。

--
作者：蕭維翰，臺大物理系畢業後逃到芝加哥，吹風吹雪之餘，做研究讀博士班。可惜離開臺灣後無海可看，只能在密西根湖旁揀一方堤岸，偽裝成看海的人。科教中心特約寫手，從事科普文章寫作。