從神經元開始的人工智慧
■當今許多器官的機械功能都能被人造取代。在小說中,各個器官組合成科學怪人,但在現實中,僅僅拼裝這些人造器官並不會變成人造人。神經元將資訊從各個器官彙整到中樞處理,這樣的「意識」或是「智慧」才是人的核心。本文從神經元開始,介紹基於神經元的人工智慧。
 撰文|陳奕廷
撰文|陳奕廷
現在許多人體器官都能被取代,例如葉克膜、人造聲帶和義肢等。科幻小說中,來自不同屍體的器官被拼湊成科學怪人,如今我們幾乎能用人工器官達成了。但是要達到「人造人」,僅僅將人造器官拼湊起來是不夠的。除了機械性的器官功能,神經元將資訊從各個器官彙整到中樞,形成俗稱的意識。
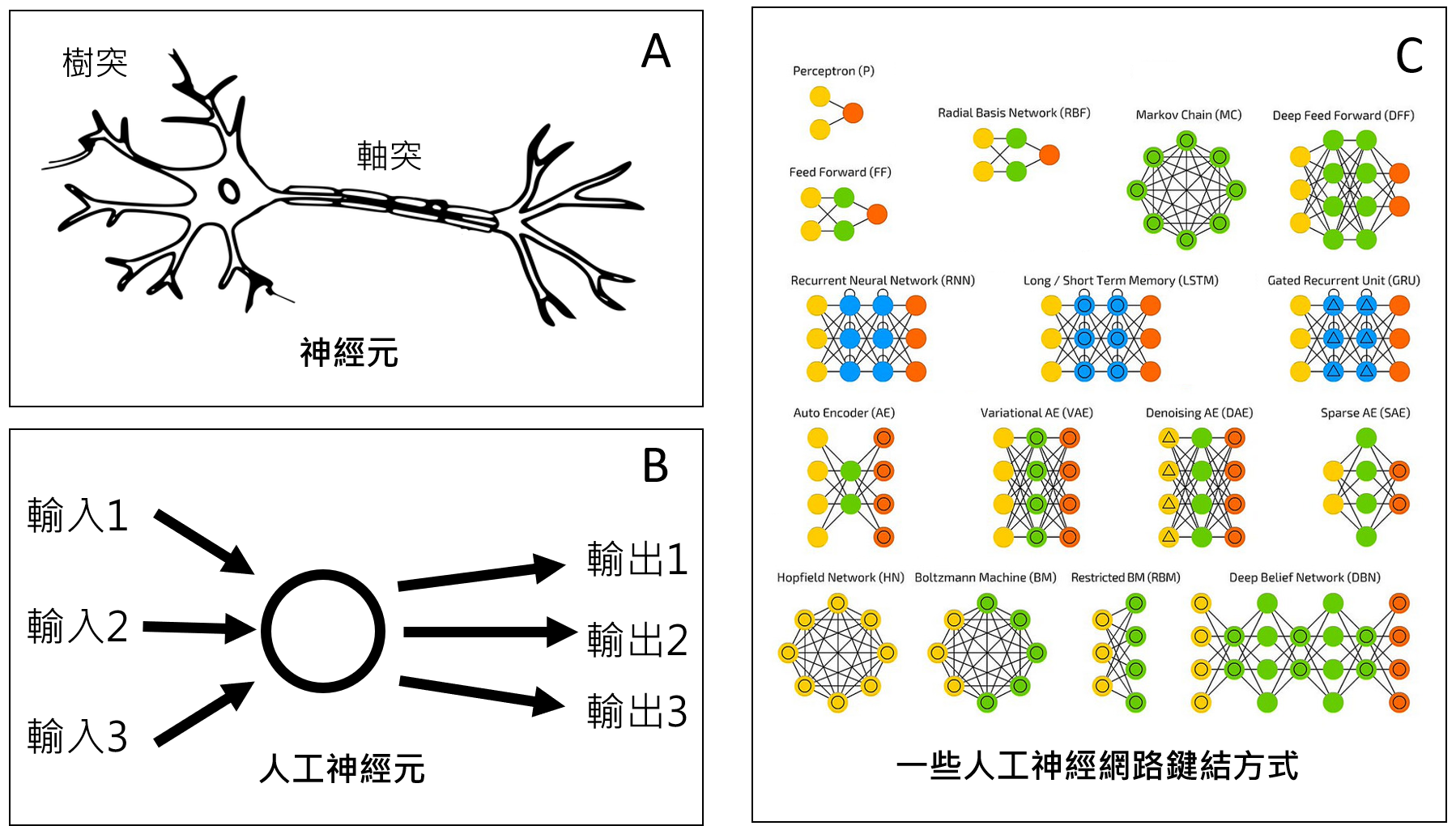
人造意識還未成熟,但千里之行始於足下,認識最基本的神經元是一個開端。如圖一A,神經元突觸分為軸突和樹突。一般認為樹突負責接收,軸突負責輸出資訊。根據對神經元的了解,科學家建立最基本的人工神經元(圖一B),嘗試解釋簡單的神經元如何產生高層次的功能。這方面的研究大致可以分成兩大類。在第一類,科學家賦予神經元幾條基本的規則,然後研究一群神經元互相溝通產生的記憶和學習等集體現象,通常被稱為計算神經科學。另一類則是單純把神經網路的架構應用在各種現實問題中,例如影像辨識、自動駕駛和玩遊戲。先要求在應用問題中表現最好,再回頭歸納出基本的規則。人工神經網路和深度學習通常屬於這一類,本文也和此相關。
●深度學習!減少變數!
神經網路有許多不同的鍵結方式(圖一C)。要「在應用問題中表現最好」,必須從所有可能的神經元鍵結方式中挑出一個最好的。如果一個網路有N個神經元,它們之間共有約N平方個鍵結。以一張256*256像素的影像為例(想像每一個像素都是一個視神經元),共有超過6萬個神經元和40億個鍵結。要從超過40億個變數中挑出一個表現最好的組合是一個困難的問題。
一種簡化的方式是限制神經元的鍵結。科學家把神經元分成10層,層層排列。單層內的神經元沒有鍵結,只有相鄰層有鍵結。如此一來總共只剩下約1/10的變數,計算速度提升10倍!這樣的神經網路架構通常被稱為「深度學習(Deep Learning)」。「深度」代表神經元被分成很多層,越深代表層數越多。而「學習」指的是從眾多變數挑出一個最佳解的數學過程。
●在電腦視覺中增加深度 - 卷積神經網路
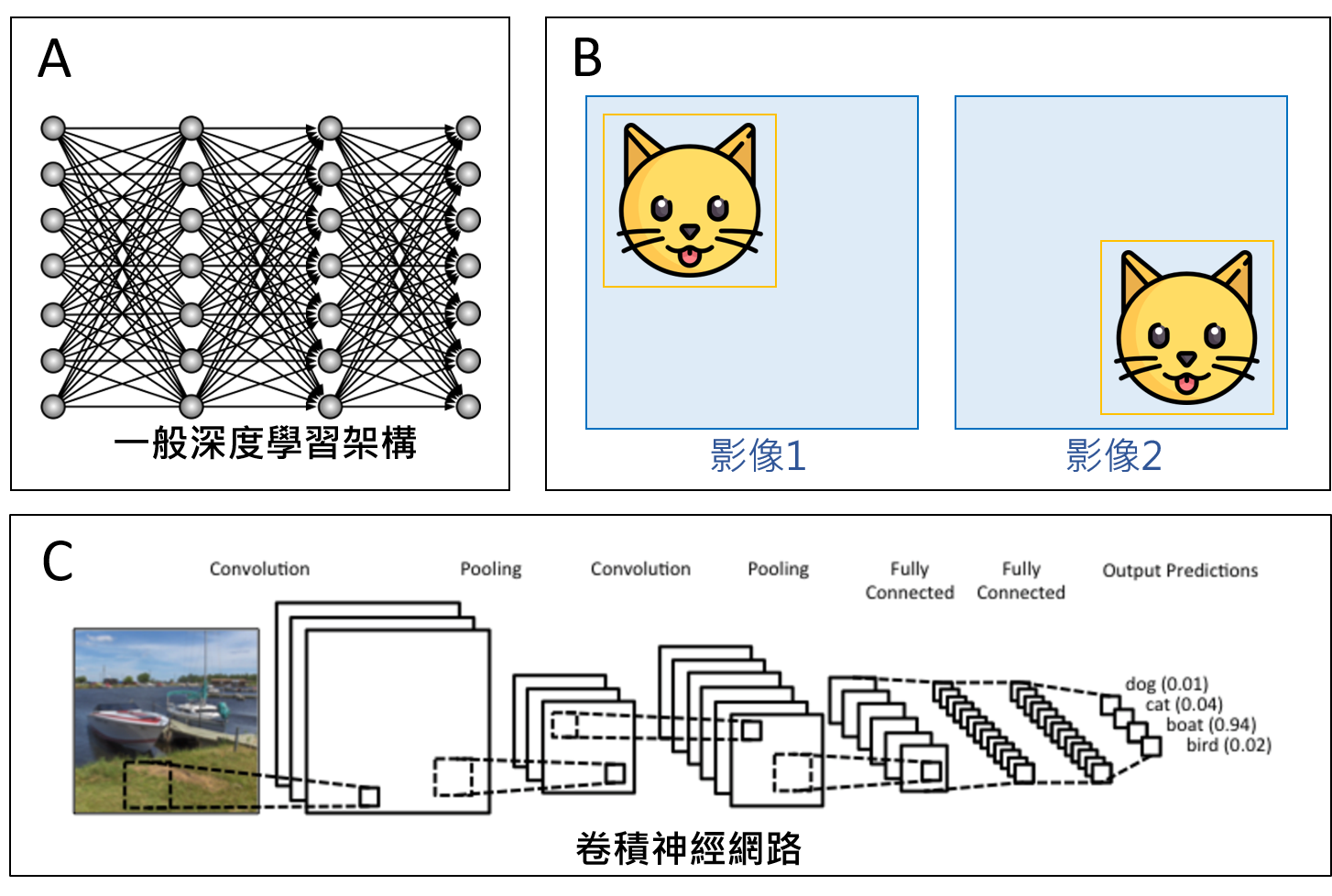
深度學習通常越深效果越好。圖二A是一個深度學習的神經網路,每一條線都是一個神經元間的鍵結,它決定資訊從一個神經元流到另一個神經元的強度,是一個變數。在電腦視覺中,人工智慧從影像中辨識出物體。以圖二B為例,貓的在影像中任何位置人工智慧都要能辨識出來。因此神經元連結方式不應該隨空間變化,也就是說兩張影像中的橘色框框附近的神經元連結方式應該要相同,而不是獨立的變數。利用這種空間關聯性把層與層之間的變數減少,就能在總變數數目不增加太多的情況下增加深度,使神經網路效果變得更好。因為它的數學細節,這種架構叫做「卷積神經網路(Convolutional Neural Network, CNN)」。一個知名的例子是英國牛津大學的視覺幾何團隊(Visual Geometry Group, VGG),用深度為16層的卷積神經網路贏得2014年的影像辨識大賽ImageNet競賽項目[參2]。
●稍微解放,效果更好 – 殘差神經網路和緊密神經網路
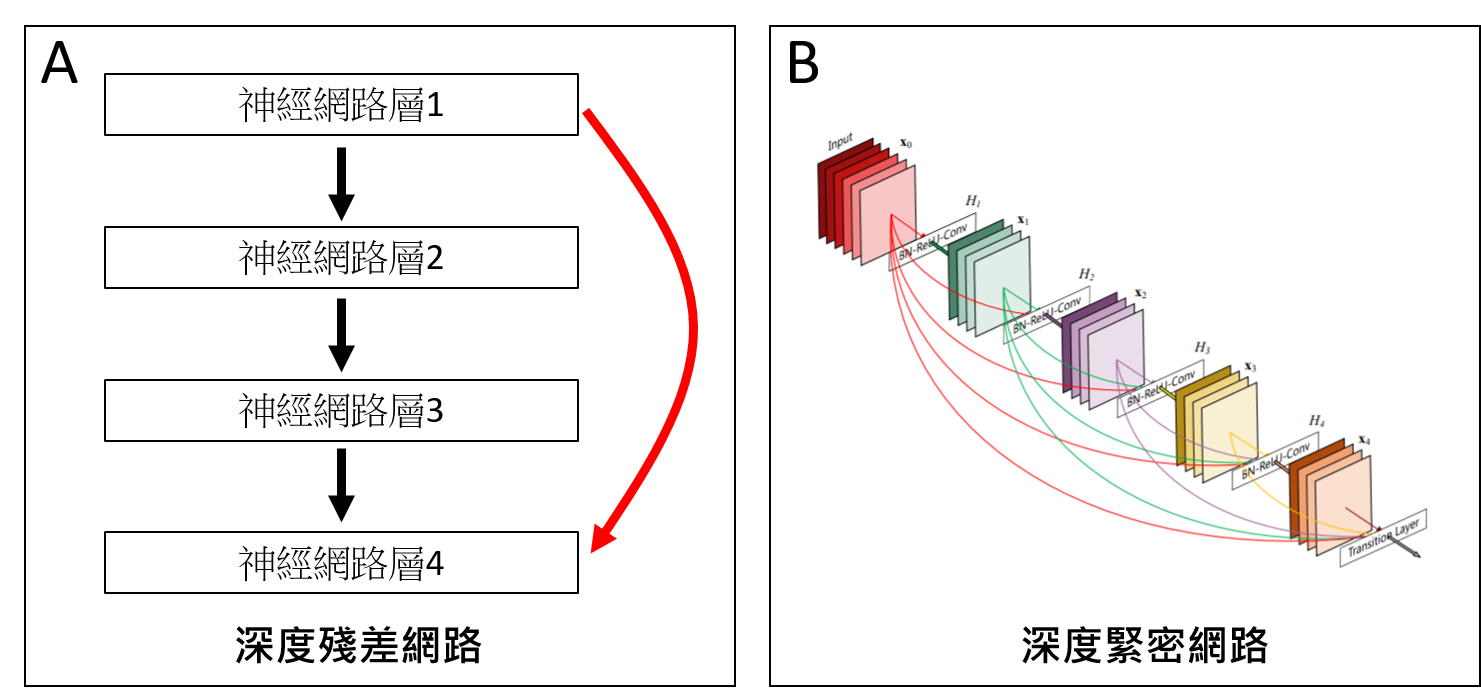
持續加深神經網路之後,效果並沒有像理論預測一樣持續增加。可能的原因是資訊在輸入層和輸出層之間的層層網路中流失了。為了解決這個問題,科學家解放「神經元只和相鄰層鍵結」這個限制。如圖三A,除了相鄰的神經層之間的鍵結,神經網路層1也跨越兩層網路層,和網路層4鍵結(圖三A紅色箭頭)。這樣的架構叫做「深度殘差網路(Deep Residual
Network)」,深度可以達到150層以上,效果比牛津大學的VGG團隊更好,贏得了2015年ImageNet競賽項目 [參3]。不久之後,深度網路被更進一步地解放。如圖三B,神經網路層不僅僅是跨越兩層相連,而是連續五層每一層都相連。這樣的架構叫做「深度緊密網路(Densely Connected Network)」,效果更好[參4]。這個方法在2017年獲得頂尖電腦視覺會議CVPR的最佳論文獎。人工神經網路是當今最熱門的人工智慧領域,今後還會持續出現各式各樣、表現更好的神經網路。
[參1] The Asimov Institute, The neural network zoo (2016)
[參2] Karen Simonyan et al., Very deep convolutional networks for large-scale image recognition, arXiv:1409.1556 (2015)
[參3] Kaiming He et al., Deep Residual Learning for Image Recognition, arXiv:1512.03385 (2015)
[參4] Gao Huang et al., Densely Connected Convolutional Networks, CVPR (2017)
--
作者:陳奕廷,台大物理系學士,史丹佛大學應用物理系博士班就讀中。
