電磁對偶（S-Duality）與歐姆定律（上）

■對偶性是物理學定律中一個很審美導向的主題，這兩篇文章中我們將討論能不能使對偶性超脫純審美的觀點，而在計算上有所貢獻。

撰文｜蕭維翰

理論學家常遇到的問題是，探討了一千零一個模型後，究竟有什麼用？譬如在前幾期對偶性的討論，許多學者們探究了許多不同模型間的等價性，但對於世人，甚至於其他分支的理論物理學家，這些「對偶」的用處並不明顯。

那一個物理理論怎麼樣算「有用」？筆者相信大多數的學者會同意其中一個關鍵是能不能計算可量測的物理量。

在這篇短文，筆者希望討論在之前介紹的電磁對偶的「可能用途」：[1]計算電導率（也就是電阻率的倒數）。

進入正文之前，我先複習（或說明）兩個小概念，來說服讀者這個可能的用處值得探究。

﹡什麼是電導 / 電阻：

這個提問意指的是給定一個模型，物理學家們怎麼計算電導。莊子曰：「請循其本。」回想在中學實驗室中，接通線路後，必須打開電源供應器，才會有電流。簡言之，改變電磁場的狀態，得到的響應就是電流。要測量電阻時，必須再調整那些電壓設定，然後量測電流的改變，才能計算電阻，也就是再度改變電磁場，從電流的改變中可以獲得電導或電阻。把這些動作抽象化：拿到一個模型，我們便觀察電磁場出現在模型的哪個地方，然後我們改變兩次電磁場，從獲得的響應可以計算電導。

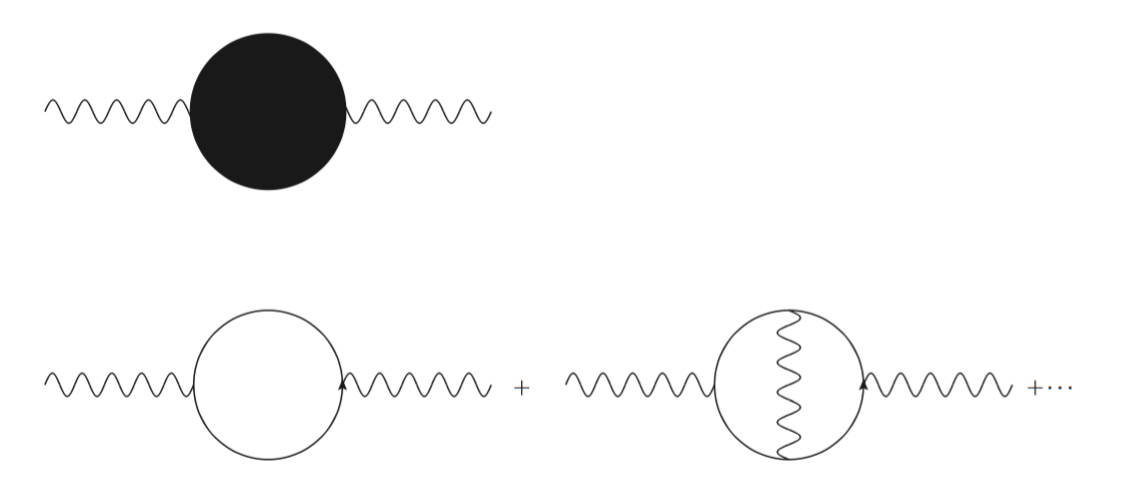
﹡費曼圖：

回憶探索講座《沒有人懂的量子力學》中，賀培銘教授曾經在投影片上播放費曼圖。在不同的問題中，一張費曼圖代表的精確意義可能不同，但約略上表示，時空中某兩點上物理量的關聯程度。以該講中的量子電動力學為例，高能物理學家們使用費曼圖的主要目的是計算當我把兩束粒子撞在一起，出現某種剩餘物質的機率。而在本文中，費曼圖的意義比較接近前兩行所概述的統計上的關聯函數。如果這樣也還太抽象，一言以蔽之，每個符號像是一塊樂高積木，將每個符號代表的公式拼湊起來，物理學家可以有效地計算一些物理量。

倘若波浪線是代表電磁場，為了計算電導，原則上我要把所有有兩根波浪線外角的費曼圖都加起來。說得容易，但即便是簡單的量子電動力學，也包含了無窮無盡，有很多很多圈圈的圖。

施溫格、費曼與朝永振一郎當初教大家怎麼好好算一個圈圈的圖就獲頒諾貝爾獎，要把包含無數圈圈的圖加總，直至今日我們依舊是無能為力。

因此從頭開始計算電導，是很困難的問題。

知道難處後，我們回頭複習電磁對偶。所謂電磁對偶性指的是，在沒有電流和電荷的狀況下，將電磁學問題中的電場換成磁場，磁場換成負的電場，整個方程式是不變的，在對偶性的第一篇中我們還提到，電荷的強度從 e 映射為 1/e，彼時我宣稱，一個強關聯的問題在此映射下變成弱關聯的問題。更有趣的是，我們知道 1 的倒數是 1，也就是這個存在一個 e 值，使得對偶的理論跟原理論一模一樣。

但這邊我得坦承，這個強弱作用的對應某種程度上是表面的，因為沒有電流與電荷，電磁作用的「強度」沒什麼實驗意義。然而，若存在電流與電荷，必須同時在問題中加入「磁荷」與「磁流」，對偶性才會保持。但是磁單極還沒被實驗所驗證，也導致表面上：有對偶時，沒交互作用，而有交互作用時，沒對偶。

為了讓電磁對偶性超越單純數學上的操弄，我們必須找到上面論述的漏洞。

一分鐘參透電磁對偶的快速答案是，電磁對偶是三維空間中馬克斯威方程式的性質。但我們知道在三維空間中有一些二維的材料，比如說石墨烯這種薄膜，上面有表面的電荷與電流。結合兩者：我們在無電荷、電流的三維空間，置入一層薄膜，其上可以有侷限在薄膜上的表面電荷與電流，從而在完整的三維世界電磁方程式具有電磁對偶性，但在薄膜上又具有交互作用，如此一來，電磁對偶便獲得一絲可利用的曙光了。

在下半集中，我們將概略描述如何透過這個性質計算電導。

 

[1] 我謹慎地說是「可能用途」，係因為能為一個模型進行計算是一回事，這個模型要貼近現實到可以被實驗實現又是另一回事。

 --
作者：蕭維翰，臺大物理系畢業後逃到芝加哥，吹風吹雪之餘，做研究讀博士班。可惜離開臺灣後無海可看，只能在密西根湖旁揀一方堤岸，偽裝成看海的人。科教中心特約寫手，從事科普文章寫作。