【大宇宙小故事】12 歐幾里得故事集
撰文|葉李華
話說兩千多年前,有個名叫歐幾里得的作家編了一本書,收錄將近五百則民間故事。
由於古代社會沒有著作權的觀念,歐氏在書中未曾提及這些故事的來源或出處。整本書從頭到尾,只有他一個人的名字,因而造成後世讀者不少誤會。
他將這本書分成十三卷,每卷收錄的故事有多有少。最少的(第二卷)只有十四個故事,最多的(第十卷)超過一百個。
這些故事發生在同一個虛擬世界,彼此有著千絲萬縷的關聯。那個世界裡只有少數生存法則,除此之外沒有任何誡律或禁忌。
在第一卷中,歐氏首先介紹二十三個經常出現的角色,再條列出主宰這個世界的十項生存法則,然後一口氣講述了四十八個故事。這些故事一律沒有題目,只有編號(I.01至I.48)。
既然那十項法則適用於整本書,其餘各卷就不必再重複。但若有新角色出現,照例會在講故事前先介紹一番。
或許是為了讓讀者更有參與感,歐氏發明了一種說故事的特殊法門:先寫出開頭和結尾,再回過頭來詳述中間過程,事實證明這個大膽嘗試非常成功。
讓我們拿I.47這個故事當例子(它是整本書最有名的一篇):
開頭:很久很久以前,有三條線段a, b, c,他們聚在一起時,會構成一個直角三角形。
結尾:終於確定他們之間有著a2+b2=c2這個關係,從此他們過著幸福快樂的日子。
過程:……(因為字數太多,僅附上歐氏手繪的插圖。)
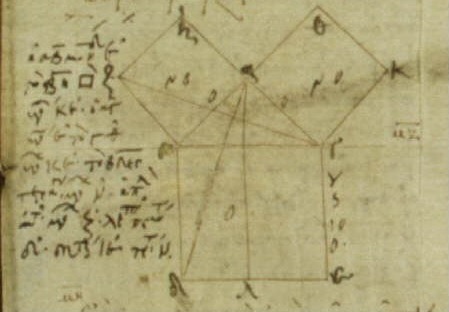
這個故事實在太有名,讀過的人不計其數。有些讀者在看完後,對那個過程並不滿意(有人覺得不夠簡潔,也有人覺得不夠曲折),於是他們採用相同的頭尾,自己構思中間的情節。累積至今,已有大約四百種不同的版本,遙遙領先第二名。
此外,這個故事還有另一項世界紀錄,讀者為它取的名字特別多,而且每個名字都頗為耐人尋味。
畢氏定理:因為據說這個故事是畢氏原創的(並非事實)。
百牛定理:因為據說畢氏寫出這個故事之後,宰了一百頭牛祭神(並非事實)。
陳子定理:因為據說這個故事是中國古代的陳子原創的(不一定是事實)。
商高定理:因為據說中國古代的商高最先發現一個特例──邊長3:4:5的直角三角形(不一定是事實)。
風車定理:因為它的插圖頗像具有三個葉片的風車(有點道理)。
雙角定理:因為上面兩個葉片看起來像一對犄角(也算有道理)。
孔雀(尾)定理:因為有人獨具慧眼,把風車看成一隻美麗的孔雀(令人自嘆不如)。
新娘椅定理:基於一個眾說紛紜、莫衷一是的原因。
勾股弦定理、勾股定理、弦定理:因為直角三角形的三個邊,中文分別稱為勾、股、弦。
在這麼多名字當中,相信大家都會同意「勾股定理」堪稱首選。可惜英文將「勾、股」都稱為「直角邊」(cathetus),所以在英語文獻中,最佳的選擇是「弦定理」(Hypotenuse theorem)。
註一(名詞對照):
《故事集》→《(幾何)原本》
生存法則→公設與公理
角色介紹→定義
故事→命題
(故事的)開頭、結尾、過程→(命題的)前提、結論、證明
註二:《原本》共有五項公設與五項公理,詳細內容如下。但從現代數學的觀點,公設與公理並無明顯區分,故可統稱為十項公理。
五項公設:
1.任意兩點之間都能畫出一條直線。
2.一個線段的兩端可以延伸任意長度。
3.使用任何圓心、任何半徑都能畫出一個圓。
4.所有的直角彼此都相等。
5.如果一條直線與另外兩條直線相交,所產生的兩對內角其中一對之和小於兩個直角,那麼上述兩條直線在無限延伸後必定相交於內角和較小的那一側。
說明:最後這項就是「平行公設」的原始版本,內容複雜且不易理解。目前通用的版本是如下的等價敘述:「在平面上有一條直線,以及線外一點,你剛好能畫出一條通過那個點且平行那條線的直線。」
五項公理:
1.分別等於某量的兩個量彼此相等。
2.相等的兩個量各加上同一個量結果仍相等。
3.相等的兩個量各減去同一個量結果仍相等。
4.能重合的物件就是相等的物件。
5.整體大於局部。
說明:上述的五項公設顯然和幾何都有直接關係;而在五項公理中,只有第四項(能重合的物件就是相等的物件)是幾何問題的專利,其餘各項則是幾何與代數皆適用。
註三:用今天的說法,《原本》中的命題分為兩大類,一是「幾何定理」,二是「幾何作圖題」。不過嚴格說來,後者只是前者的特例,換言之也是定理。例如《原本》中的第一個命題就是作圖題,仍可將它寫成如下的故事:
開頭:很久很久以前,某人要執行一件艱難的任務,能使用的工具只有一把圓規和一支沒有刻度的直尺。
結尾:他終於設法根據給定的長度畫出一個等邊三角形,從此過著幸福快樂的日子。
過程:……
註四:在歐氏幾何中,作圖題只能使用圓規和沒有刻度的直尺,因此留下所謂的「三大難題」:
1.給你一個任何角度的夾角,請你將它等分成三個角。
2.給你一個立方體,請你將它的邊長延伸,做出一個體積剛好是兩倍的立方體。
3.給你一個圓,請你畫出一個正方形,使得方圓的面積相等。
以現代眼光來看,這三個題目都是不可能的任務,換言之,數學家能夠嚴格證明它們根本無解。或許正因為如此,這三題並未收錄於《原本》中。
