【探索15-2】混沌與秩序：由 Logistic map 談起

講師｜東華大學應用數學系 班榮超教授
撰文｜陳文翊

有些自然界的物體，大至像雲、海岸線，小至像微血管網、花椰菜，它們的形狀不能用簡單、經典的形狀去分類，例如方形跟圓形，但仔細去觀察，會發現它們看似複雜的外觀，在任意小的尺度下的細小結構，其實是由簡單的幾何形狀所組成的，神奇的是，在不同的尺度下會持續出現類似的幾何形狀，這樣的情況為自相似性(self-similarity)。數學家想要了解，複雜的表象是不是由甚麼簡單不變的機制，從這些細微的結構演變而來？

●Logistic map
從Robert May分析的單峰映射(Logistic map)說起，它是一種二次的多項式多項式

在這裡需要先說明映射(map)的概念，存在一個函數跟初始值 ，將這個初始值 帶入函數得到 ，再將 帶入函數得到 ……，如此不斷重複下去。在分析單峰映射時，會在原本的圖上再加一條線 x=y ，如此迭代的過程可以一目了然。單峰映射原本被用作人口學的模型， 是介於0跟1之間，用來代表第n年的人口數目；r是一個影響人口成長的參數，根據繁殖和餓死率所得，在這裡我們討論 0≤ r ≤4 的情況。

當 r<1 時，經過多次迭代後發現 →0；當1<r<3時，發現 會趨近一個固定值(attracting fixed point)。當r越來越大，像是 r=3.3 時，會發現迭代多次以後 會在兩個值之間震盪(period-2 cycle)；r=3.5 時， 則會在四個值之間震盪(period-4 cycle)。為了分析不同 r 的情況，我們將不同的 r 與其對應的 (n→∞)作圖，此圖稱分歧圖(Bifurcation diagram)。當參數 r 變化時，可以發現一開始幾乎所有的點都會趨近二周期點，再來是四周期點、八週期點等等，而在有些參數中我們可以看出任一個點出發後都不會停在某一個週期點，在這些參數中因為我們沒有辦法追蹤它的終極行為，所以通常用機率或者是測度的語言來描述這些參數的行為， 回到這個區間的機率有多大。在此定義兩個新的名詞，一個是穩定參數，代表在此參數下的 會被某個週期點所吸引；一個是隨機參數，代表在此參數下 的終極行為最後不會停在某些點。總的來說，當 r ≈ 3.57 時，映射會變得越來越混亂、迭代後不能趨向某些點，但是當 r > 3.57，會發現圖呈現不能預期的、有秩序(穩定參數)及混亂(隨機參數)交錯出現的情況，這就是一開始所提，一個簡單機制既基本卻又能製造出相當複雜的現象。同時當我們放大分歧圖來看，比如像是r ≈ 3.83 選擇時不斷地放大，會發現原本分歧圖的模樣會不斷出現，這情況也是我們一開始提的自相似性。

如此想問，單峰映射有一般性嗎？也就是說可以用探討單峰映射的過程去了解其他的混沌現象嗎？首先 John Guckenheimer 跟 Michal Misiurewicz 證明任何單峰映射加上一些很寬的條件，即會和某個成長的映射拓樸共軛(topological conjugate)；接著 John Milnor 跟 William Thurston 也提出定理，說明幾乎所有的單峰映射都和成長映射中的某參數有相同的動態行為，簡單來說是研究單峰映射會是基本、簡單且具有代表性的一類函數。

另外還有其他問題，其一是隨機參數是否夠多？在這裡夠多的意思是，當我們將隨機參數收集起來，用尺去量是否可以量到大於0的長度？也稱它是否有正的勒白格測度(Lebesgue measure)。之後由 Michael Benedicks、Lennart Carleson 與 Michael Jacobson 證明隨機參數的確有正的勒白格測度。其二是在參數集[0, 4]中，穩定參數是不是稠密的？Mikhail Lyubich、Jacek Graczyk 等人分別證明穩定參數確實是稠密的，另外也得知穩定參數經得起擾動，這個意思是如果確定某個參數是穩定參數，則選取一個稍微遠離該參數一點點的參數，它也會是穩定參數，然而隨機參數則否，不能保證遠離該參數一點點是否能再選到隨機參數。其三是若將選取穩定參數的機率與隨機參數的機率加起來會不會是一？ Mikhail Lyubich 證出，再扣掉一個測度零的集合之後，在0與1間的區間中任意選取一個參數，它不是穩定參數就是隨機參數。不過其實除了這兩者外還有其他的參數，只不過它們整體的勒白格測度是0。

●描述混沌
然後是我們要怎麼描述混沌？這裡有兩個概念。第一個是如James. A. Yorke與Tien-Yien Li合寫的論文Periodic 3 Implies Chaos描述，若 f:R→R 是一個連續函數，且f有一個週期三的點，則

(1)   對任何n都存在週期n的週期點

(2)   存在一個不可數的子集S，對其中任兩點x、y我們有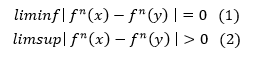

(3)   對任何一個週期點P以及S內的點x，我們有

式(1)的意思是在不斷迭代的過程中，任兩點的軌跡無窮多次會無限接近；式(2)的意思是這兩個點終究會分開；式(3)的意思是，在S裡面的點絕對不會被某個週期點吸引，也就是它不會停在某個固定的位置。而滿足這些條件的集合S，它的行為體現的混沌。

 

第二個是Devaney Chaos，所描述的三個條件：

(1)   對初始條件敏感(sensitive dependence)，在集合U裡面的任兩點，經過幾次迭代後，它們之間的距離會越來越大。

(2)   系統具傳遞性(topological transitivity)，給兩個集合U跟V，存在一個次數n，使得U在系統n次迭代後總會和V有交集。

(3)   稠密的週期點(Dense periodic orbits)，稠密的週期點其實是說明這系統是亂中有序，因為週期點是個有序、有規則的狀態，它希望系統裡面不只是亂，而是亂中有序。

順道一提，這個概念其中兩個定義可以推出另外一個定義。

●結語
其實至今還未有一個所有人都認同的定義，又混沌只說它全部都是混亂的其實有些粗糙，它事實上是部分有序的，如前面所述的單峰映射，有機率一的機會要不是選到隨機參數就是穩定參數，系統中交織穿插簡單結構與複雜結構。總括來說簡單的機制可產生出複雜的現象，又混沌和秩序是密不可分的。

 

參考資料：
1. 班榮超，淺談動力系統中的禍福相倚，數理人文第六期
2. Steven H. Strogatz, Nonlinear Dynamics and Chaos

--
本文整理自：105/4/9 由班榮超教授在臺大思亮館國際會議廳所主講之「簡單的開始，卻通往複雜？！」演講內容。