【探索十】現實生活的模擬農場──漫談生態系中的族群數量變化

第七講‧特稿

■ 「當系統複雜時，思考方向就要改變。從另一個角度去思考問題。」──劉維中老師正是利用「模型」來抽象描述我們的現實世界，揣摩食物網形成的可能機制。

撰文│郭冠廷

對現實世界的抽象描述—如何建立「理論」？
生態模型的建立，可以從最簡單的四則運算開始。N_t代表 t 時間點的族群數量，IN_Δt   代表族群在 Δt 期間所增加的量，OUT_Δt   代表族群在Δt  期間所減少的量。就是時間點的族群數量。N _t+Δt 就是 t+Δt  時間點的族群數量。

 

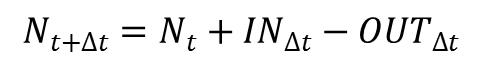
而理論的重點就在於，如何去描述 IN_Δt  和 OUT_Δt  ？我們假設每個個體在單位時間可以產生b個後代 b·N_t ·Δt，而在單位時間有d 比例的個體會死亡 d·N_t ·Δt。如此，我們就得到族群的「出生與死亡模型」：

 

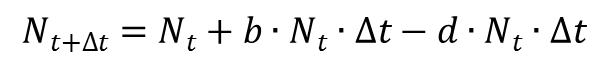
而我們根據 Δt 的長短，又可以分為Δt =1的離散型模型（Discrete time）和 Δt 非常小（ Δt ~0）的連續型模型（Continuous time）兩類。我們只要給定初始值N0 和參數b、d，就可以繪製出多組模型的結果。我們以N_t 對時間 t作圖，利用曲線圖來表示族群數量的變化。充滿變異性和不確定性的現實世界為解釋真實世界的數據，我們建立「隨機模型（Stochastic）」，用來描述變異性和不確定性：一、到下次發生事情的時間要等多久？也就是上述的Δt 。二、到下次發生事情的時候什麼有可能會發生？就上述的出生死亡模型而言，此模型中所發生的「事情」只有兩種可能：出生、死亡。加入參數後的結果，出乎我們的預期，數量對時間作圖本是一條水平線（族群數量持平）的圖表，電腦卻模擬出「在出生率等於死亡率的情況下，族群有可能滅亡。」為什麼呢？老師解釋：「族群數量很少的時候，族群會容易滅亡。」

 

替簡易模型增加變數

當族群數量增加時，個體就會愈來愈難找到食物。所以用來描述族群在單位時間中個體死亡比例的d 就會變成： d=d₀+d₁·N_t 。

 

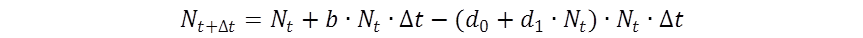
而這組模型中，假若是離散型的時間間隔（Δt =1）。簡單的單物種模型，就有相當豐富的現象。當b=1的時候，族群數量會呈現指數增加，而到一定的值後會穩定下來。可是當b=2的之後，會呈現震盪後趨於一個穩定值的過程。b=2.5 時，族群數量會在二個點之間震盪。b=2.6時，則會在四點震盪（4-point cycles）。而隨著b值增加，震盪的點逐漸增加。電腦模擬的結果告訴我們，b值增加最終的結果，族群數量會完全失序（chaotic）。

但是，在連續模型（ Δt ~0）中，b值的增加對單物種數量的影響，不會呈現任何週期性變化，隨著時間，最終都會穩定到一個固定的值。

 

尋找平衡點

這種較複雜的出生、死亡模型，是屬於一種自律（自調）模型。模型的結果是讓族群數量往某特定的數值逼近，或者是在某些數值之間震盪。這些值我們稱為「平衡點（equilibrium point）」。

當族群數量維持在平衡點 N* 不再變化時[1]，我們以離散模型（Δt =1）的平衡點 N* 為例，試著解出 N* 。

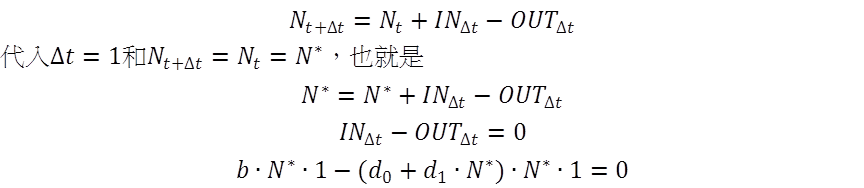
雙物種如何能夠共存？

我們假設兩種物種A和物種B利用相同的資源，我們可以得到物種A和物種B各自的出生死亡模型。

因為物種之間的競爭力需要加以描述，我們引進參數 α _BA 和 α _AB。α _BA 代表每物種B的個體數量相當於物種A的個體數量。假若α _BA =3，就代表一個物種B相當於三個物種A的個體，代表物種B佔有優勢。

物種A的Zero-isocline是二維空間當中的一條曲線，用來描述物種A和物種B數量的變化 N_A-N_B。在此線（N_A-N_B =0）上物種A的族群變化量是0，而線的一方的物種A的族群數量變化是增加，另一側物種A的族群數量變化是減少的。同理，我們也能繪製出物種B的Zero-isocline。

因著 α _BA和 α _AB 數值的不同，兩條線之間的關係有數種：物種A和物種B共存、物種B獨贏，以及只有一個物種贏（怎麼贏要看出發點）。

雙物種共存的條件，是物種自己給自己的負作用，要大於給另一個物種的副作用。「兩個團體內如果都有內鬨，就沒有時間去攻擊另一個團體，如此一來雙方就能夠共存。」

 

獵物（X）和獵殺者（Y）模型

我們從出生死亡模型出發。獵物X的死亡率因為遭獵殺而增加。獵殺者Y獵殺的所得透過參數轉換成獵殺者Y的出生率。並找出獵物和獵殺者的Zero-isocline。我們可以發現得出來的圖形，平均向量的變化，似乎在「繞圈圈」。族群數量的變化對時間作圖，有週期性變化（neutral cycles），這個週期性變化，會取決於「出發點」。不同的初始值會導致不同的結果。

但是，如果這個模型是「隨機模型」，為什麼電腦模擬的結果卻沒有辦法出現週期性變化？「因為族群數量很少的時候，族群會容易滅亡。」因此，當我們加入不確定性和變異性後，模型很難呈現永恆的週期性數量變化。

 

如何讓物種能夠共存？

一、兩個獵殺者共同競爭相同的獵物，兩位獵殺者之間可以共存嗎？

電腦模擬的結果，其中一個獵殺者會因為獵物的數量有限，而遭遇滅亡。

但是現實世界當中，卻有許多競爭相同獵物的獵殺者得以共存。可能的原因有：兩個獵殺者生存在不同的棲息地，或是食用相同獵物不同的成長階段。也可能是獵殺者之間有著「群聚效應（aggrcgation）」，造成資源（獵物）區分。

所以，競爭者的共存與否，取決於他們競爭資源（獵物）的相似程度。

二、雙獵物被相同的獵殺者所獵殺，要相互競爭「沒天敵的空間」，則這兩被獵殺的物種，可以共存嗎？

電腦模擬的結果，其中一個獵物必定會走向滅完。

不過真實自然界中有不同的獵物共存的例子。這可能歸功於「庇護所（refuge）」的功勞，讓獵物不完全被獵殺者所獵殺，造成物種共存的效應。

三、食物鏈模型。物種A被物種B吃，物種B又被物種C吃。這種情況下，三物種可以共存嗎？

我們得到的模擬結果是：可以共存。物種C會壓制物種B，造就物種A會無限成長。「上級獵殺者把下級獵物從中間獵殺者釋放出來」。

 

多物種模型

從上述的「例子一」[2]當中我們得知，當物種B和物種C共同競爭物種A時，物種B和物種C無法共存。因此，我們嘗試加入物種D來改變局勢。老師提出一個可能性：加入物種B或物種C的天敵物種D，讓物種D去壓制物種B或物種C其中一方。物種D壓制的結果，反而造就物種B和物種C得以共存。

 

最後，維中老師替上述的研究方法做一個歸結。我們可以延伸今天所看到的模型，模擬自然界中複雜的食性關係。

 

誰是重要的物種？

我們利用不同的中心性指標[3]來進行排行：「通常重要的物種不等於是稀有物種。」這想法提供我們對稀有物種保育的新方向。例如：海洋生態系當中最重要的物種是誰？就電腦模擬的結果而言，並非海豚、鯊魚，而是中型烏賊。

 

為什麼食物網會需要構造的複雜性？

重要的物種通常是維持生態系統（食物網）完整性的角色，而重要物種的消失，會讓整個生態系統（食物網）瓦解。自然界中必然會有另一物種，來避免單一物種的滅亡，連帶造成物種的大量滅亡。所以，物種的重要性（species centrality）和物種網路位置的獨特性（species positional uniqueness），應該是負相關的。

 

複雜的食物網背後是否有簡單的生成機制？

「植物吸收陽光，變成草食性動物的食物，草食性動物又是肉食性動物的食物……。」老師利用這則想法，來進行模擬。系統中有R個未使用的資源（食性位階0），N個物種將會出現（生態系中起始狀態沒有任何生物）。

隨著N和R的增加，就會產生「複雜」的食物網。乍看之下很像現實世界的食物網。因此，老師就使用中興大學林幸助老師所提供，核二廠國勝灣的田野調查數據來進行應證。該食物網物種之間的食性關係有36個連結，而食性位階的層級數為8。

令人傷心地發現，食性關係數最高只能模擬到28。而食性位階的層級數雖然可以到8，但是當層級數為8時，食性關係數目卻相當的低。

老師秉持研究者的精神，加入「馬太效應」的假設：「大者恆大。」也就是：一個有較多資源的物種，會有更多經驗找更多的資源。可惜結果並不如預期。

研究的路途是要愈挫愈勇的。從另一個角度切入，老師改採「使用效應」的兩個假想。假想一：或許物種比較喜歡吃接近他們食性位階的食物。例如：獅子比較喜歡吃牛羊，不喜歡吃昆蟲。假想二：高階物種較有移動能力，所以較容易到達我們的生態系統。因此，高階的食物會比低階的食物更容易被新來的物種使用。也成功模擬出國勝灣的食物網模型。

「馬太效應」，是讓食物網朝水平方向發展的機制。而「使用效應」，是讓食物網朝著垂直方向發展的機制。而國勝灣生態系的發展過程，就由電腦模擬農場，得知可能是由「使用效應」而非「馬太效應」所產生。

 

 

 

--- 本文整理自：102/12/07下午由劉維中老師在臺大應力所國際演講廳所主講之「現實生活的模擬農場──漫談生態系中的族群數量變化」的演講內容

延伸閱讀：臺大科學教育發展中心探索基礎科學講座2013年12月7日第七講〈現實生活的模擬農場──漫談生態系中的族群數量變化〉全程影音

責任編輯：Vita Chen