當人工智慧結合量子電腦

臺大光電工程所碩士班 王勻遠 編譯

量子特性解決二元制機器學習瓶頸

現今當紅的機器學期演算法已被用來解決許多問題，如圖像辨識、行為預測等。然而一旦輸入更龐大的圖像資料（像素更多），亦或預測人們具有「相干性」的認知行為，都將使得傳統機器學習變得窒礙難行，耗費龐大的運算資源，更無法進行準確預測。

對於以神經網路為底的機器學習而言，圖像辨識就像試圖解決如Ax=b此一矩陣方程式的線性代數問題。在圖像像素動輒百萬的情況下，A與x的維度，或可理解為變數與向量數目都在百萬以上。而在現今多數仍為二元制（binary）的計算機系統中，輸入的資料更被離散化，所需記憶體容量會比原資料的維度再大上好幾個數量級，相關運算顯得曠日廢時。

然而，若利用量子系統中的疊加態（superposition of states）來描述，將x轉換為量子波函數 ，x的所有資訊都可被包含在波函數 的線性組合（├ |x_i ⟩，i=0、1、2⋯⋯ ）中（圖1A）；而每一項 的權重係數也不再侷限以「離散」，而可以「連續」形式表達，更貼近現實中問題的本質[1、2]，例如呈連續變化的像素明暗、由三原色疊加而成的色彩。

另一個瓶頸，則是人類認知行為的預測，尤其那些具相干性的行為。所謂「相干性」，即代表問題或事件呈現的次序，會影響人們的判斷或行為結果。舉例來說，1997年的一份美國政治民調要求受測者依次表態，是否認為當時的民主黨候選人比爾‧柯林頓與艾爾·高爾值得信任。研究人員發現：若將兩位候選人的詢問次序對調，受測者認為兩者皆「值得信任」的機率大增。此類人類行為，無疑徒增傳統機器學習的預測難度。

所幸，量子運算本身便須考量交換律（commute）。我們可將受測者的兩種回答─「是（Y）」與「否（N）」─當作兩量子基底態├ |Y⟩、├ |N⟩ 的線性疊加，而兩個問題A與B作為量子運算符 （Quantum Operator），如此便可初步描繪出受測者回覆「是」或「否」兩狀態的機率幅度，進而預測受測者的答案。假設A、B不滿足交換律，即AB不等於BA，則需加入量子修正[1]（圖1B）。在量子運算的輔助下，機器學習便能更全面地，也更輕易地克服這些預測瓶頸。 

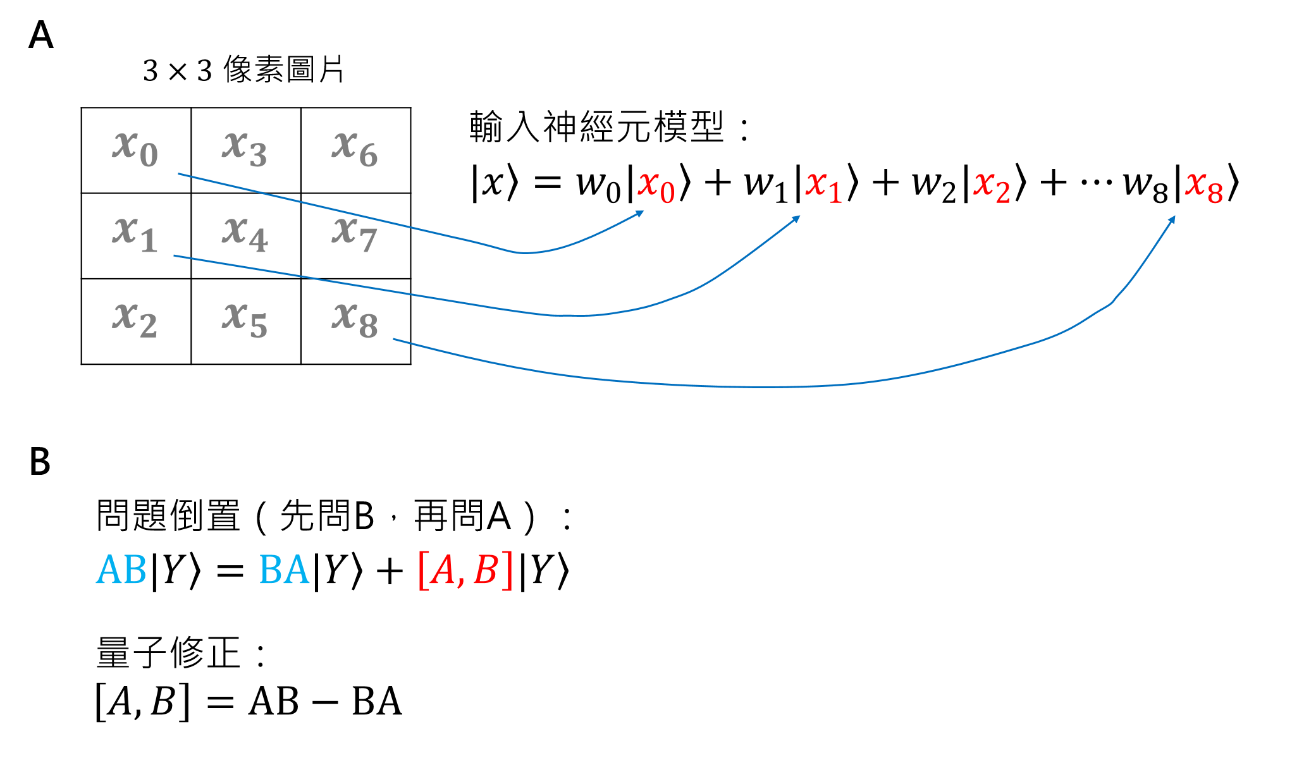
圖1. A以神經網路圖像辨識模型為例，輸入神經元由一個多維度的量子態表示，其中係數（權重）w_i可代表像素i的明暗。B舉例，問題倒置對受測者回答「是」的影響，須計入量子修正；在量子力學裡，若A、B算符分別代表位置及動量，則[A, B]=iħ，i為單位虛數，ħ為約化普朗克常數。

硬體問題

雖說有了量子電腦的輔助，人工智慧的發展看似如虎添翼、前程錦繡，但若缺乏相應的硬體設備，也是巧婦難為無米之炊。

現階段量子元件的開發，主要還是基於量子位元（Qubit）。不同於非0即1的離散二元系統，量子位元 同時是0與1的疊加態（ ├ |x⟩=├ w₀ |0⟩+├ w₁ |1⟩），其代表的資訊層次更密集，也蘊含更多可能性。然，也正因如此，量子位元對外在環境相當敏感，0和1兩個態的比重易受溫度干擾，因此當前多種量子元件須在極低溫的環境下操作。這些對雜訊免疫力不高的量子系統，有悖於當初為抵抗雜訊影響，而設計數位編碼的初衷。

而上述問題的背後，其實還有更深層的隱憂。在更進階的量子演算法中，單一量子位元可以是二個維度 ( 狀態 ) 以上的量子疊加態，例如├ |x⟩=├ w₀ |x₀ ⟩+├ w₁ |x₁ ⟩+├ w₂ |x₂ ⟩+⋯├ w_n |x_n ⟩ 。只是當中所牽涉的變數繁多，除了前述的溫度干擾外，如何開發出能實現此一構想的量子元件，目前仍是一個有待解決的開放性問題。

再者，每一次資料讀取，都將使得量子波函數塌縮（wave function Collapse）；易言之，量子位元中所儲存的資訊被干擾了。因此量子運算系統仍需準備n個 ├ |x⟩量子位元，才能準確知道完整的機率分布、進行預測[1]，成為量子演算法的一大缺陷。幸運的是，許多科學家仍致力銜接量子演算法與現實硬體設備間的鴻溝，一旦成功，已然炙手可熱的機器學習將有爆炸性的進展。

參考資料

1.  Alejandro Perdomo-Ortiz, et al., “Opportunities and challenges for quantum-assisted machine learning in near-term quantum computers,” IOPscience, Quantum Science and Technology, Vol. 3, Number 3, March 20, 2018.
2. Scott Aaronson, “Read the fine print,” Nature Physics, vol. 11, p.p. 291–293, April, 2015.