沒有階層的神經網路─ODE net

編譯/黃柏瑋
階層式神經網路
以圖像辨識為例,我們可以輸入一堆狗的照片,讓神經網路從中摸索共同特徵,從而成為判斷「圖片中是否有狗」的依據。只是,理想終究不敵現實。在真實世界中,單一特徵或標準其實並不夠嚴謹,極有可能導致過高的失誤率。例如,我們不能單以「是否具有耷拉的大耳朵」來判定照片中的動物是否為狗,因為像是吉娃娃的耳朵是直挺的,而大象的耳朵卻是下垂的,類似例外不勝枚舉。
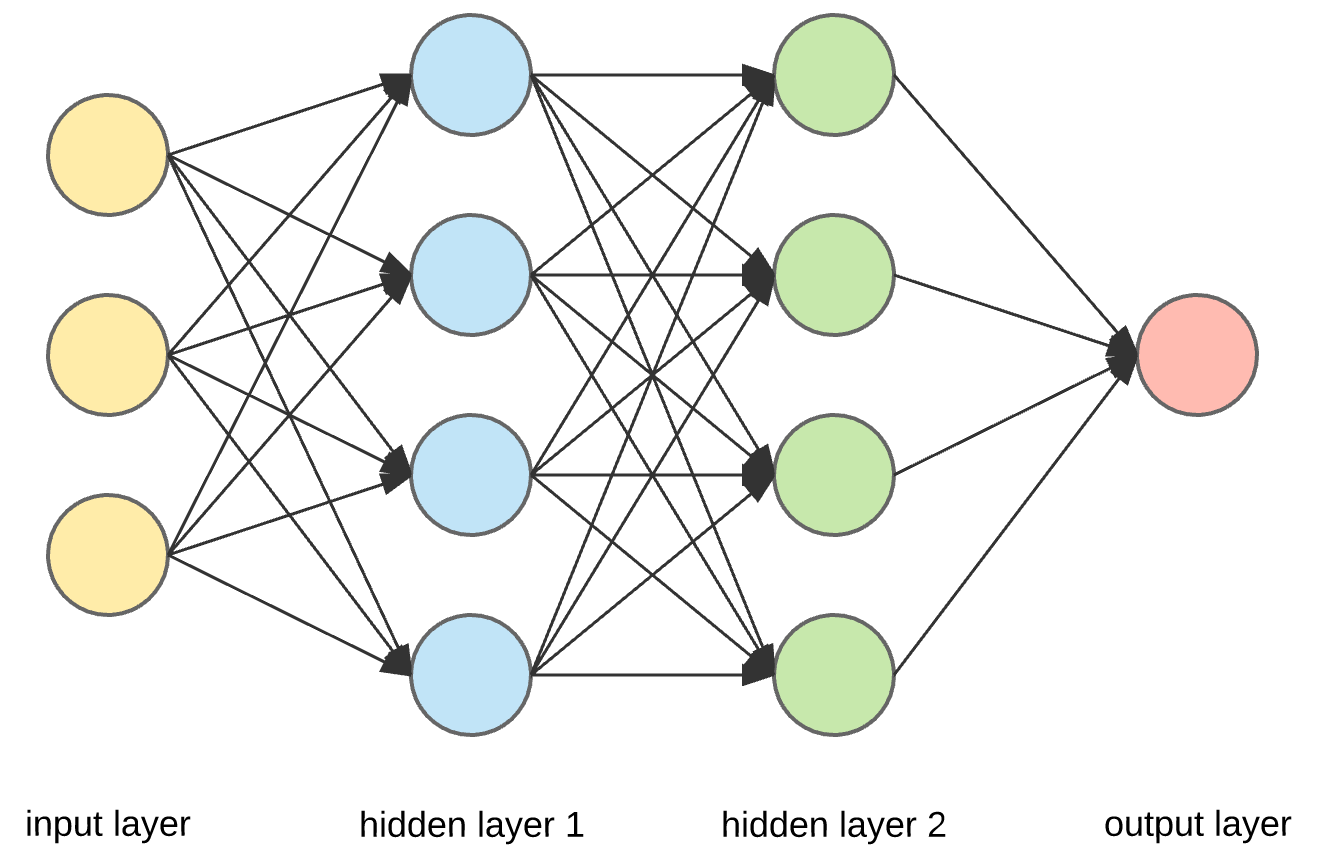
圖一、傳統階層式神經網路。
為此,電腦科學家發展出「階層」的概念,用以修正太過粗糙的判斷策略。如圖一所示,整個系統可以大致分為三層:負責接收圖片資料的「輸入層」(input layer)、進行一連串分析的「隱藏層」(hidden layer)以及作出判斷結果的「輸出層」(output layer),整個神經網路的核心主要在於「隱藏層」。
為了抓取更細緻的特徵,隱藏層可以有多個層次,例如隱藏第一層(hidden layer 1)可以以特定公式,從照片中挑選出那些與狗最相關的像素;接著,第二層(hidden layer 2)藉由另一個公式,由這些像素中建構出一個更具體的圖樣,例如判斷圖片中的動物是否長有鬍鬚或耳朵;依此類推,而後每一階層隨著計算越精細、複雜,逐步推敲出更細緻、具體的特徵,也更能精確判斷圖中生物。
當然,隱藏層中每一節點(類比於生物神經系統中的單一神經元)間的連結方式,也會影響系統的執行效率以及應用,造就了現今各式各樣的神經網路,包括較簡單的「前饋神經網路」(Feedforward neural network,FNN)、「深度神經網路」(Deep Neural Network,DNN)、「卷積神經網路」(Convolutional neural network,CNN)和「遞歸神經網路」(Regression neural network,RNN)等。
連續問題
然而,當我們所輸入的資料與所求的結果都是隨時間而連續變動時,傳統神經網路中階層的離散性卻成了一大阻礙。假設我們要以傳統神經網路預測患者未來的健康狀況,勢必得將病歷資料以年為單位作分類,但這使得「每個月看一次病」和「一年中某單月看病十二次」對於機器而言其實毫無差別,而導致評估上的誤差。(你或許認為以日為單位便可巧妙地避免這類問題,但難保患者的病情不會在短時間內急遽變化,一天看兩、三次病!)
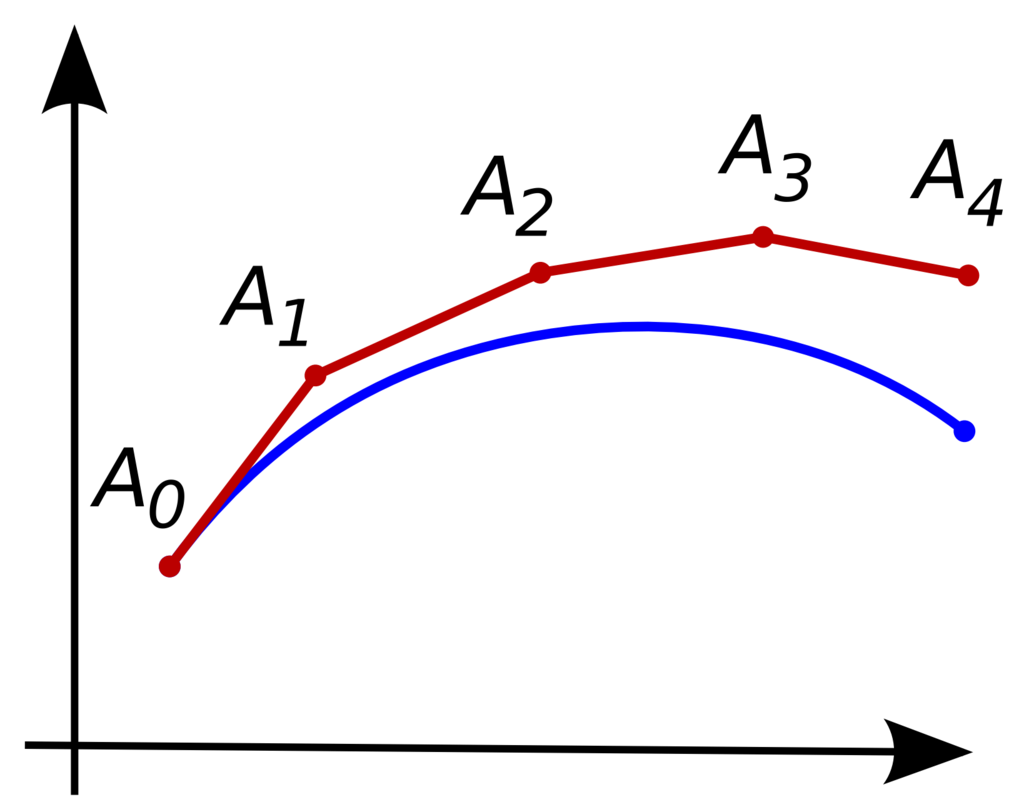
圖二、歐拉方法。
換個角度思考,連續型的判斷可被製成一條連續曲線,而資料的離散化和數值分析的歐拉方法(Euler method)其實有著異曲同工之妙。先來說說歐拉方法,如圖二所示,當我們想要還原藍色的連續曲線(所求),但僅有起始狀態A0和微分方程式時,我們可以先找出A0上的切線,並選一個固定間距(Δt)定出A1,再重複前述的動作直到終點。其中,若節點越多(Δt越小),誤差值就會越小,也越貼近預期結果。
事實上,歐拉方法中的每個步驟就好比神經系統中不同階層的工作,某相鄰的兩個節點可被視為某一階層的輸入和輸出。同理,在處理連續型問題時,若神經網路的隱藏層越厚,或將時間段切得越細,所得到的誤差就會越小,結果的價值也會越高;不過,這也表示若要達到百分之百精確,我們需要無限多的隱藏階層。
為此,多倫多大學Duvenaud教授和研究夥伴重新設計原先的神經系統,捨棄原有的「階層」概念,轉而選擇解決極限和無窮問題的利器—微積分,以解決離散化的問題。本質上來說,微積分就是一門研究變化的學問,因此若我們將輸入的資料轉為常微積分方程,再尋找出比歐拉方法更有效、更精準的工具來估算未知的方程式,便可提升人工智慧的效能。
ODE net
這類的設計雖早已擺脫「網路」的概念,但基於傳統考量,研究人員還是將其名為「常微分方程網路」(Ordinary Differential Equation net,ODE net)。
一個更平易近人些的例子,這就像小提琴與鋼琴間的差異:小提琴作為弦樂器,理論上可以拉出音域範圍內任何頻率的音,輕易展現滑音;但發聲原理較接近敲擊樂器的鋼琴,卻只能盡力模擬滑音效果,音符間仍還是「粒粒分明」。由傳統分層神經網路到ODE net的演進,就像把鋼琴換成小提琴。單就連續問題而言,ODE net更具前瞻性。
另外, ODE net的訓練方式也有所不同。當我們在訓練傳統神經網路時,可以在開始之前指定階層數目,並在結束後得知準確度;但在訓練ODE net之前,我們能指定的卻是模型的準確度,並依此找出最有效率的方式進行訓練,而代價是我們無法知曉訓練所需的時間長度,這也是將來選擇此法時,需要慎重考量和斟酌的部分。
ODE net目前只是基本架構,仍待後續研究為其添上血肉。即使如此,作為「時序模型」(time-series model)應用於如保健醫療領域上,ODE net的前景仍令人拭目以待。
編譯來源
K. Hao, “A radical new neural network design could overcome big challenges in AI”, MIT Technology Review, 12 Dec 2018.
參考資料
A. Colyer, “Neural Ordinary Differential Equations”, The Morning Paper, 9 Jan 2019.
(本文由教育部補助「AI報報─AI科普推廣計畫」執行團隊編譯)
