Pomeranchuk 不穩定性與量子霍爾效應中的向列相
■理論物理學家們想透過費米液體理論中的 Pomaranchuk 不穩定性來說明量子霍爾效應中觀測到的向列相(nematic phase)物理,第一個數值計算,告訴我們這是可能的。
撰文|蕭維翰
上文中我們討論這一兩年被提出的量子霍爾效應實驗結果,其中一個亮點在於:實驗學家觀測到 v=5/2 的量子霍爾態,在外加強壓之下,可以從一個有能隙的絕緣態進入一個沒有能隙的物質態,並且旋轉對稱性被自發地破壞了。白話地講,即便我們施加的強壓沒有方向性的差異,但測量到的電阻值在 x 方向與 y 方向有極大的差異。目前這被認為是 v=5/2 量子霍爾態可以從一個拓樸態(像 Moore-Read / Pfaffian 波函數這樣的基態)進入到對稱破壞態(上文所討論的向列相(nematic phase))的觀測證據。
我們也指出,眼下這個現象還沒有完備的理論解釋,但我們有一些提議來說明哪些物理機制在定性上會導致這些結果。在本文中我們將說明其中一個機制—由費米液體中的 Pomeranchuk 不穩定性造成的向列相,與複合費米子的蘭道參數(Landau parameter)有沒有辦法導致這個不穩定性。
之所以跟費米液體有關係,是因為其中一個理論解釋是透過複合費米子(composite fermion)形成的費米液體(Fermi liquid)來描述霍爾量子態,並透過破壞圓形的費米面(Fermi surface)來破壞旋轉對稱。(這也是為什麼筆者之前會想要花篇幅解釋負荷費米子與費米液體等概念,因為他們無所不在。)
回顧我們在討論 v=5/2 量子霍爾態的直觀圖像時,我們說在蘭道階(Landau level)半填滿時,複合費米子們會形成一個費米海,在旋轉對稱性沒有被破壞時,每個費米子的準粒子能量是動量的函數,而費米海在動量空間會形成一個球,在二維空間就是一個圓形。
要讓它變形,我們必須讓這個圓形不穩定。讀者在文獻中若讀到所謂讓費米面不穩定,意思是讓這個球狀的費米海不再是具有最低能量的狀態。一個有名的方法就是讓費米子們形成超導體,則在費米面附近的費米子們就會形成古柏對(Cooper pair)而凝聚。另外一種考量是調整模型中的一些參數讓別的幾何形狀比圓形擁有更低的能量。在之前的文章中我們也說明過,費米液體理論裡的交互作用是由一系列的現象學參數,蘭道參數(Landau parameters)來代表,在文獻中我們常寫成 F1,F2…,Fℓ ,其中下標的數字 ℓ 代表這個散射頻道的角動量數。
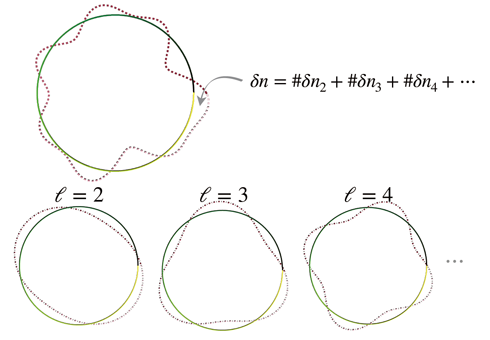
用圖像來說明的話,我們可以考慮底下這樣一個腳本。首先我們從原來圓形分佈的費米子密度開始,然後稍微改變一下這個分佈。在圖一中我們畫出了不同頻道 ℓ 所製造出的分佈形狀。要檢驗有沒有其他形狀的費米子分佈可以有更低的能量,想法也很簡單 — 我們就計算新粒子分佈跟舊粒子分佈之間能量差,看看哪個分佈的能量比較低。如果被變形後的費米海反而有較低的能量,我們就稱費米面有一個不穩定性。
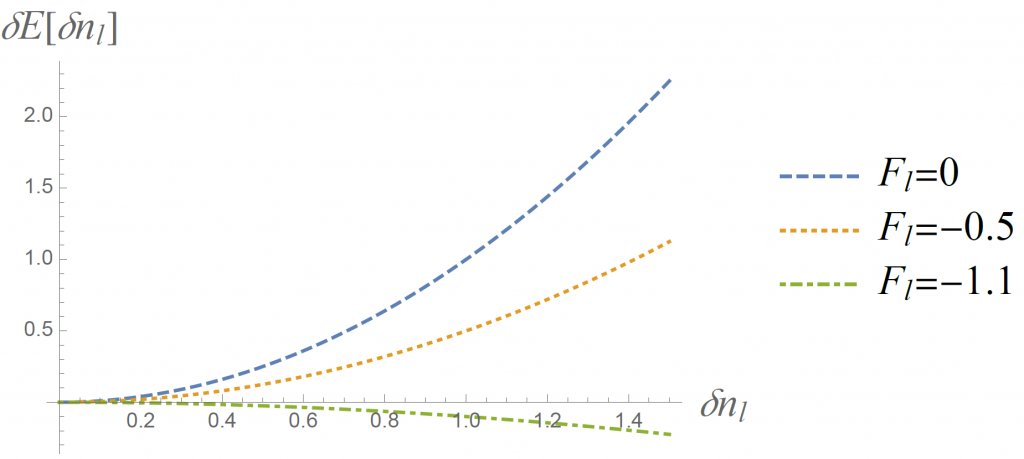
因為費米子間的交互作用都用蘭道參數表示,讀者們可以想像分佈的能量也會依賴於蘭道參數。在圖二中,我們把能量差 δE 對二維費米子分佈的變形量 δn 作圖,並且我們針對某個頻道 ℓ 畫出在費米液體理論框架下不同量值的蘭道參數 Fℓ 對能量差的影響。結論就是在 Fℓ= -1 這個點,能量差由正轉負,變形後的分佈反而比原來的圓形分佈穩定,這就是標題裡所提的 Pomeranchuk 不穩定性。
特別是當 ℓ = 2 時,新的基態分佈是一個向列態。
假若我們想要把這個故事套用到量子霍爾跟向列態的相變化上,我們就要問,那麼這個不穩定性有可能在蘭道階中實現嗎?更實際點說,我們有辦法從一個夠真實的物理系統出發,進而計算霍爾系統中的蘭道參數,然後驗證這是一個可能的物理機制嗎?
今年二月由新近諾貝爾獎得主 D. Haldane 所帶領的團隊使用變分蒙地卡羅(variational Monte Carlo)的數值方法,計算一個被靜電屏蔽的庫倫交互作用所對應的蘭道參數 [1]。他們分別計算了n=0,1,2 的蘭道階,對應到量子態 v=1/2,5/2,9/2,在不同系統「厚度」下,ℓ=2,3,4,5 的蘭道參數。
他們主要的發現如下:
(i) 在n=0,(v=1/2) 的部分,完全沒有 Pomeranchuk 不穩定性的跡象。
(ii) 在n=1,2 而且 ℓ = 2 時,當系統厚度低於某一個程度,F2 都會掉到 -1 以下,其中 n=2 不穩定的範圍又比 n=1 大。這和實驗上所觀測到的也定性吻合:在較高的蘭道階中,旋轉對稱較容易自發被破壞。
(iii) 在其他散射的頻道 ℓ=3,4,5 蘭道參數都不足以啟動對應的 Pomeranchuk 不穩定性 。
雖然他們沒辦法將複合費米子的超導體效應納入計算,而且在定量上的預測也還跟實驗不盡相符合(譬如從數值結果判斷,v=5/2,應該不用特別條件也能啟動 Pomeranchuk 不穩定性,但實驗上卻需要特殊的壓力。)但他們的研究是第一次有團隊以計算指出,從微觀旋轉對稱的位能計算出的蘭道參數也能引發對稱性的破壞,並且他們的結果意味著,當系統的厚度越小,越接近真實的二維系統,那麼在高層蘭道階系統其實是更不可避免的往向列相靠攏。
參考資料:[1] K. Lee, J. Shao, E.-A. Kim, F. D. M. Haldane, and E. H. Rezayi, Pomeranchuk instability of composite Fermi liquid, arXiv-preprint: 1802.08261 (2018).
--
作者:蕭維翰,臺大物理系畢業後逃到芝加哥,吹風吹雪之餘,做研究讀博士班。可惜離開臺灣後無海可看,只能在密西根湖旁揀一方堤岸,偽裝成看海的人。科教中心特約寫手,從事科普文章寫作。
