沈君山解說黑體輻射（二）

■如何用比較直覺的概念，了解黑體輻射是什麼？

 撰文｜高涌泉

沈君山在40多年前寫了〈3K黑體輻射〉，其中完全沒有說明何謂「黑體」，也就是他根本不提黑體輻射這名詞的來由，而將重心全然放在黑體輻射究竟是什麼。他在簡短的第一節「總說」之後，就這麼開始第二節「黑體輻射」：「要了解3K黑體輻射，先得明瞭黑體輻射一詞的物理意義。這個名詞讀者們也許早已耳熟能詳，大一的教科書裡用數學方程式把它定義得很嚴密，我在這兒再用通俗的話解釋一遍，希望能給讀者們一個比較直覺的概念。」為了說明這個「比較直覺的概念」是什麼，我引述他接下來的兩段文字（僅在幾處調整了一些文字）：

「讓我們先從平衡狀態一詞說起，譬如在一個光滑的大理石盒子裡，散散落落的放上一些白色的撞球彈子，然後把一顆紅彈子用力彈進去（假設彈性碰撞）。剛開始只有紅彈子在跑，白彈子都靜止不動，但這狀態顯然並不平衡，因為彈子們互相碰撞，每撞一次，本來不動或者雖動而能量較低的，就會增加些速度，本來跑得快而能量大的，就會減少些速度，過一段時間再去觀察這一堆彈子，不論白的、紅的，大家的能量都差不多了——當然並不是每顆彈子的能量都完全一樣，有高一點的，也有低一點的，若用電眼把每顆彈子在『同一瞬間』的能量記錄下來，會發覺彈子的能量E分佈是依據e ^-E/E0這一公式（所推導而出），此式即所謂的波茲曼分佈律。」

「E₀代表每顆球的平均能量（大理石盒子是二維空間，所以E₀是E的平均值，在一般三維空間裡，E 的平均值是(3/2)E₀），把E₀除上一個常數（稱波茲曼常數k＝1.38×10^-10erg/K），便是這些撞球的運動溫度T，即E₀＝kT。到了這個地步，撞球動能的分佈便不再隨時間改變，也就是說不但此一瞬間的分佈如是，過一段時間後的另一時間，其分佈亦如是。這種狀態就叫平衡狀態，因為整體而言，彈子的情況到了最穩定的狀態，不再改變。但是這只是統計的不變，每顆球的速度其實隨時都在因撞擊而改變。」所以沈君山在說明平衡狀態時，也介紹了溫度的定義（概念）是如何出現的。

有了較易想像的彈子為例，他接著引導我們想像一群也處於平衡狀態的光子。不過在此之前，他得先強調平衡狀態的出現得仰賴粒子的相互作用，所以他說：「大理石盒子裡撞球的運動遲早會平衡，但達到平衡的快慢則要看相互間的作用。假若把大理石盒子裡的撞球換上數目相同的小彈子，則達到平衡所需的時間顯而易見比大撞球長得多，因為小彈子面積小，許久才撞到一下，而撞球面積大，很快就會碰頭。達到平衡所需時間大致和撞擊頻率成反比……原子與原子、電子與電子都互相作用……唯有光子和光子並不相互作用（極高能量的光子，能產生正負電子者例外）。把一堆能量不同的光子放在一起，如果不摻雜外物，無論過多久還是會維持原狀。光子只和帶電體作用，所以要使光子達到平衡，一定要和物質摻雜在一起，使吸收放射循環不息，時間既久物質與光子就達到平衡，大家的平均能量都一樣，只是物質顆粒在一般狀態下，能量依波茲曼分佈，光子則依普朗克律分佈，此乃因光子是沒有質量的玻色子，和一般物質顆粒的性質不同。這種依據普朗克律分佈的輻射，也叫黑體輻射。」

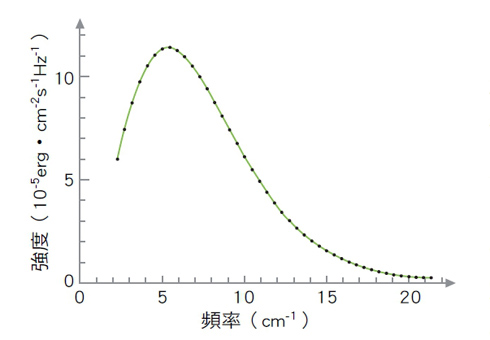
沈君山要講的就是宇宙中存在著溫度約為3K（精確值為2.725K）的「宇宙微波背景（黑體）輻射」。上圖顯示的是10餘年前物理學家用人造衛星測量所得此輻射的強度隨頻率的變化，其關係與普朗克律公式完全相符！

--本文原刊載於《科學人》形上集。