測試波函數的意義與玻色版本的 Moore-Read 波函數

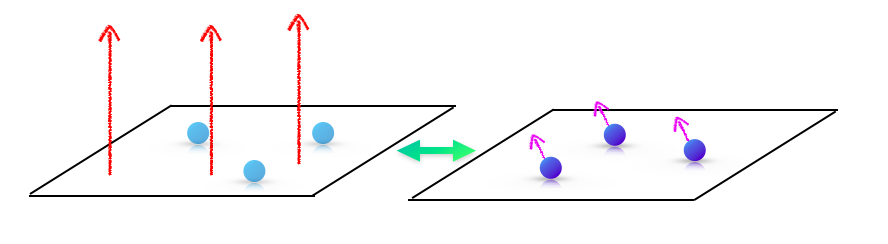
■之前跟大家介紹的測試波函數不僅僅在霍爾物理中有用，即便在玻色愛因斯坦凝聚態的研究中也有貢獻。

撰文｜蕭維翰

有鑒於在先前幾篇已經提到了 Moore-Read 波函數的名字，筆者便想不如一鼓作氣再多說一點跟霍爾物理中測試波函數相關的事情。

要不要拿測試波函數來當科普題材一直筆者自己很掙扎的問題。在真正的物理研究中它們隨處可見，尤其在人們解析手法受限的強關聯問題中，如霍爾效應的物理。但另一方面它們卻也是極端技術性的，如果我不寫下任何方程式，我甚至很難跟大家說明定性上會發生什麼事，遑論是定量的結果。

但我覺得 Laughlin 波函數跟 Moore-Read 波函數這類的測試波函數，或許值得做一次嘗試性的討論。

首先，讓我在重新講解一次測試波函數的概念。

在面對很多個粒子的薛丁格方程式的時候，現有的計算能力通常不允許我們直接解開它。然而我們當問題的答案有一些直覺的時候，譬如我們約略知道問題的基態該有什麼物理性質時，有經驗的物理學家們可以將這些性質轉變成實際的數學條件，寫下一個測試的函數。

這聽起來有點神秘。第一次看見在量子霍爾物理中這些測試波函數的人，十之八九都會驚訝於這些發明人的創造力。所幸在這個圈子裡看問題看久了後，就會知道在數學裡，有一大群函數都長得這副模樣，有些恰巧具備了我們喜愛的物理性質，從而脫穎而出被加上了名字，而剩下的還在待價而沽。

言歸正傳，因此一個測試波函數通常不是真的波函數，但倘若我們有辦法藉由一些測試來確定這個函數跟真的基態波函數「夠像」的時候，我們便可以藉由了解測試波函數的性質，來了解實際基態的性質。

上面的意思是說，無論是 Laughlin 波函數或者 Moore-Read 波函數，都不是某個庫倫作用的模型的真正解。

但有趣的是，我們其實可以建立一些模型，使得 Laughlin 波函數或者 Moore-Read 波函數是這些模型的真正基態。某種程度上，這有點像先射箭再畫靶。譬如說當你寫下 Laughlin 波函數，你會發現當兩個粒子的座標重疊的時候，這個波函數的值為零。也就是說如果你考慮一種很短距離的交互作用，只有兩個粒子碰在一起時才有數值，那麼當計算這個系統在 Laughlin 波函數這個狀態底下的能量時，一定會得到 0—因為你建構的位能只在兩座標重疊時才有值，但 Laughlin 波函數在座標重疊時沒有值。Moore-Read 波函數也有類似的詮釋，它其實是可以被當成某一類三體交互作用的基態波函數，也就是當三個粒子相遇時才有值位能。

這樣的波函數也不僅僅在霍爾效應裡有用。譬如在筆者以前曾經討論過旋轉中的玻色愛因斯坦凝聚態（ Bose-Einstein condensate, BEC）。由於在旋轉座標中，角動量（跟科氏力差不多意思）在數學上跟外加磁場是等效的，在極高速的旋轉之下，物理學家們期待這些問題會趨向於另一個霍爾效應的問題。

但我們也知道，僅管玻色子的能譜也能形成蘭道階，但這絕對不會是原來的霍爾效應問題，因為在玻色愛因斯坦凝聚態中的基本粒子們是玻色子。回憶很久之前對於霍爾效應的半古典解釋，筆者引用了庖立不相容原理（Pauli exclusion principle），因而面對玻色子的「霍爾效應」，我們甚至失去了半古典的圖像跟直覺。

失去定性的圖像對於解釋物理工作固然很不理想，所幸這並不阻止我們先在數學上進行一些計算。玻色子不遵守不相容原理，但在 2 維空間，物理學家可以使用之前討論的磁通量附著技巧將他們變成複合費米子加上一單位的磁通量，玻色子的分數霍爾效應就變成了複合費米子的整數霍爾效應。這個技巧預測了玻色子分數霍爾效應的 （我用下標 b 代表這是玻色子的填充分數。）。

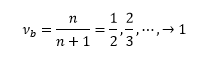
其中 n 是複合費米子所填滿的蘭道階數。這時候我們可以更仔細地看兩個極限，也就是 v_b=1/2 與 v_b=1。前者代表複合費米子指填滿了一個蘭道階，而後者是填滿無限個蘭道階，也就是費米海（Fermi sea）。若我們回頭從費米子的分數霍爾效應借一點靈感，前者對應到的應該要是玻色版本的 Laughlin 波函數。而後者則比較不明朗，如果我們把它類比到費米子的 v_f=1/2，那基態應該是個無能隙的費米液體（Fermi liquid）。倘若我們把它類比到費米子的 v_f=5/2，那基態應該要是個有能隙的複合費米子超導態。

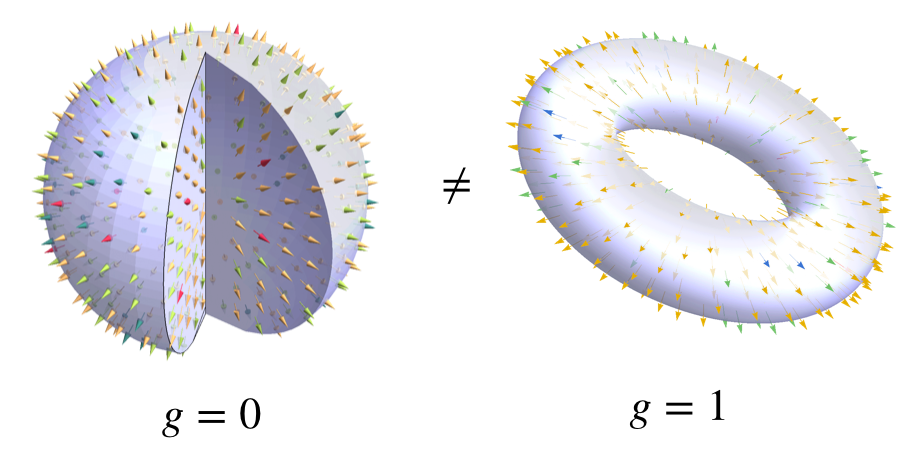
要解決直覺上的分歧，得訴諸實際的計算。目前比較廣為接受的數值結果是，若考慮短距離的交互作用，則v_b=1的基態具有能階，並且跟玻色版本的 Moore-Read (Pfaffian) 波函數有很大的重疊。更有支持力的證據是，當我們把系統放到具有不同拓樸的空間上做計算，基態的簡併程度會跟空間的拓樸有關，說明了這個基態是具有拓樸序的 [1]。

希望透過這次的介紹，讓大家稍稍多了解一點測試波函數的意義，以及一個他們在純粹霍爾效應以外的應用。

 

參考資料：

[1] N. R. Cooper, Rapidly rotating atomic gases, Advances in Physics 57, 539 (2008).

--
作者：蕭維翰，臺大物理系畢業後逃到芝加哥，吹風吹雪之餘，做研究讀博士班。可惜離開臺灣後無海可看，只能在密西根湖旁揀一方堤岸，偽裝成看海的人。科教中心特約寫手，從事科普文章寫作。