v=5/2 量子霍爾態之謎（中）

■誰是描述v=5/2基態的波函數？曾經我們都快要相信就是 Pfaffian 波函數，直到 ...... 。

撰文｜蕭維翰

誰是描述v=5/2基態的波函數？曾經我們都快要相信就是 Pfaffian 波函數，直到 ...... 。

在前文中我們複習了量子霍爾效應，並在文章的下半段介紹 v=5/2 態，並說明為什麼他是個有趣的問題，並且用一個問題結尾 —— 我們有沒有一個類似 Laughlin 波函數的試驗波函數來代表這個狀態。而在本文中我們將更深入地討論這個懸問。

在這之前，筆者想先釐清前文的一段敘述。

上文的後段中，我提及這個v=5/2態可以想成是複合費米子形成的超導體態，並且我聲稱，這些複合費米子必須以 p 、f 波或其他奇數角動量的方式配對。我必須承認在寫下這段敘述時，我心中已經有某些波函數，並且這個宣告暗自地假設了 (1) 在那一層蘭道階的電子們的自旋都在同一個方向上，而且 (2) 複合費米子是非相對論性的費米子。第一個條件在文中也有提及，但其實最早的研究中，學者們也曾考慮過電子自旋未極化的狀況，在那樣的假設底下，複合費米子也能以 s 波配對。關於實驗上對這個假設的最新報導，可以參考 [1]。第二個假設則是近年來引起許多討論，因為在芝加哥大學的 Son 在 2015 年提出複合費米子其實也可以是狄拉克費米子 [2]，這個狄拉克費米子可以形成 s 波配對。

為了不混淆大家，在接下來的討論中，若無特別說明，我都將維持 (1) 跟 (2) 的假設。

●Pfaffian 波函數

回到 v=5/2量子態，我們的問題是：有沒有一個像 Laughlin 波函數的波函數，可以幫助我們了解這個量子態？在 1991 到 2007 間，在數值結果上呼聲最高的候選人是所謂的 Moore-Read 波函數 [3]，又稱作 Pfaffian 態（簡寫成 Pf）。

Moore 跟 Read 顯然是提出的兩位物理學家，那什麼是 Pfaffian?

寫作的時候我才發現這個詞沒有中文的維基網頁。用最簡單的方法講，給定一個偶數維度的反對稱矩陣，這個矩陣的 Pfaffian 約略就是行列式開根號。這個名稱與波函數的具體形式有關係，在後續的段落中，我都將之簡寫為 Pf 態。

除了是v=5/2的強力候選人，Pf 態本身就是一個故事很豐富的波函數。甚至可以說，人們寄託於v=5/2量子霍爾態的許多想像，都來自於 Pf 態。以下就讓我們來陳述它的性質。

(i) 分數電荷：回想首先聲名大噪的 Laughlin 波函數，這個波函數其中一個貢獻就是，他說明了在系統中的準粒子可以帶有分數電荷，以v=1/3的量子霍爾態而言，裡面的準粒子帶的電荷是q=e/3 ，也就是三分之一的電子電荷。利用 Pf 波函數，Moore 跟 Read 也可以進行類似的計算，並且發現這裡面的準粒子有

q=e/4

(ii)馬約拉納（Majorana）費米子：在粒子物理的定義中，馬約拉納費米子擁有自己是自己的反粒子這種特殊的性質。在凝態物理中，由於數學上形式的類似，普遍認為在超導體中的博格柳博夫（Bogoliubov）粒子在某些條件下可以是馬約拉納粒子。其中一個場合就是在 p 波超導體的「漩渦」^[1]中，一如前面重複闡述的，Pf 態是一個 p 波超導體。也因此若他真的描述了v=5/2態，那這個霍爾系統就也變成搜尋馬約拉納費米子的平臺之一。

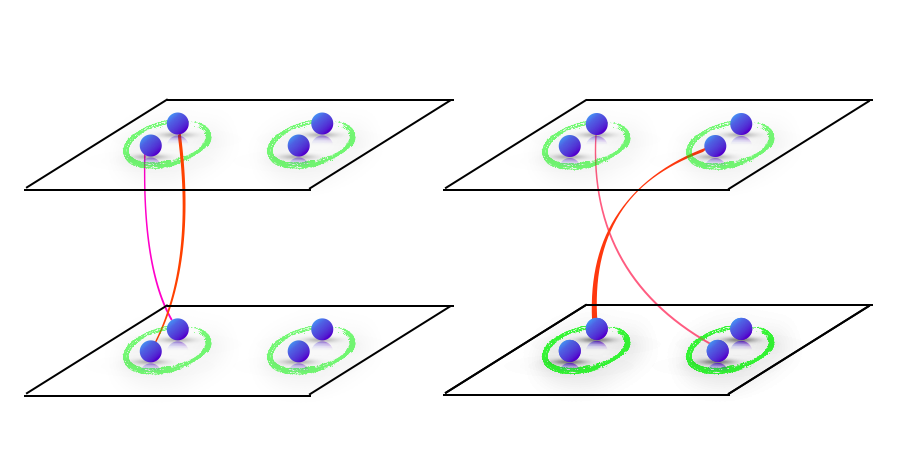
(iii) 非阿貝爾任意子（non-Abelian anyon）：任意子（anyon）是在 2+1 維系統中一個特殊的概念。出發點是，考慮在空間的兩個粒子，我們輸送其中一個粒子，讓它繞過另外一個粒子，然後我們問，描述這兩個粒子的波函數在這個過程前跟過程後有什麼差？在 3 維空間中，其實沒有辦法真的去界定說一個粒子真的「繞過」了另一個。但在 2 維空間是有辦法的。最一般的狀況是，這個波函數會被乘上一個絕對值為 1 的複數，從而可以推論，當我們交換兩個粒子的位置（繞半圈），波函數也會被乘上一個絕對值為 1 的複數。當這個數不是 +1（玻色子）或 -1 （費米子）時，我們稱它為（阿貝爾）任意子（(abelian) anyon）。在這邊 abelian 的意思是真的只有乘上一個複數。Pf 態裡面具有的是更神秘的 non-Abelian 任意子 [4]。

它的意義是，首先，給定某個能量，這個系統得有很多簡併態（degenerate states），也就是說很多具備不同量子數的狀態都具備這個能量，而重要的點，是這些簡併態不能經由局部的操作（local operation）從一個跑到另外一個。非阿貝爾任意子的概念是，當我們編織這些任意子的時空軌跡時，結果不只是在波函數上乘上一些複數，而讓我們從其中一個簡併態跳到另外一個簡併態。

●Pf or Not?：

以上這些性質，在學理上可以被應用在量子計算，又因為 Pf 態是呼聲最高的v=5/2候選人之一，也因此某些學者會認為這個霍爾態也有機會變成實驗量子計算的平臺（但我們現在知道這並不是一個領先的提議。）

但筆者想要在下篇接續的故事是，在 2007 年左右，有其他學者提出了跟 Pf 態不分伯仲的 anti-Pfaffian 波函數，更甚者，在 2015 年， Son [2] 提出 PH-Pfaffian 態，究竟這些不同的 Pfaffian 誰更受真實世界青睞？且待下回分解。

 

參考資料：
[1] Md. Shafayat Hossain et al, Phys. Rev. Lett. 120, 256601 (2018).
[2] D. T. Son, Phys. Rev. X 5, 031027 (2015).
[3] G. Moore, and N. Read, Nucl. Phys. B360, 362 (1991).
[4] D. A. Ivanov, Phys. Rev. Lett. 86, 268 (2001).

註解：
^[1] 不是真的視覺上的漩渦，但要解釋這個概念，會需要另外一篇獨立的文章。

--
作者：蕭維翰，臺大物理系畢業後逃到芝加哥，吹風吹雪之餘，做研究讀博士班。可惜離開臺灣後無海可看，只能在密西根湖旁揀一方堤岸，偽裝成看海的人。科教中心特約寫手，從事科普文章寫作。