費曼之於固態物理：超導與超流

撰文｜蕭維翰

在學界內，費曼是出了名的不愛寫文章，當然那個時代學術的市場還不是那麼競爭，加上他在學術的聲望，讓他可以耐心將有趣的工作完成到一定水準再與世人分享。然而，大家如果查閱他的著作年表，會發現他在 1953-1955 年間密集推出了好幾篇文章 [1-4]，同時間他的勁敵 Schwinger 正費心力將量子電動力學雕塑成更優雅工整的形式，費曼卻暫時放下粒子物理，將他路徑積分與費曼圖的技術帶到在凝態物理的超流體氦液（4He）問題中。再往下翻閱年表，在 1957 的 Review of Modern Physics ，我們也能找到費曼的一篇「超流性與超導性」[5]，談論那個時代理論物理學家對這兩種物質態的了解。

 

在本專題的最後一篇文章，筆者便嘗試談談費曼在這些領域的表現。尤其是後者——超導體問題上的發揮。

費曼在 1953-1954 的文章中主要的結果包括 (i) 嘗試計算超流氦的熱力學性質，以及 (ii) 提出一個近似波函數去解釋實驗上看到的「旋子」（ roton）。

第一個結果比較技術性。在物理概念上，費曼指出超流現象和玻色愛因斯坦凝聚態的相似處，而為了妥善計算熱力學量，他將那時候還問世不久的路徑積分技巧應用到了統計物理問題內，並將交互作用效果濃縮到氦原子的等效質量內。

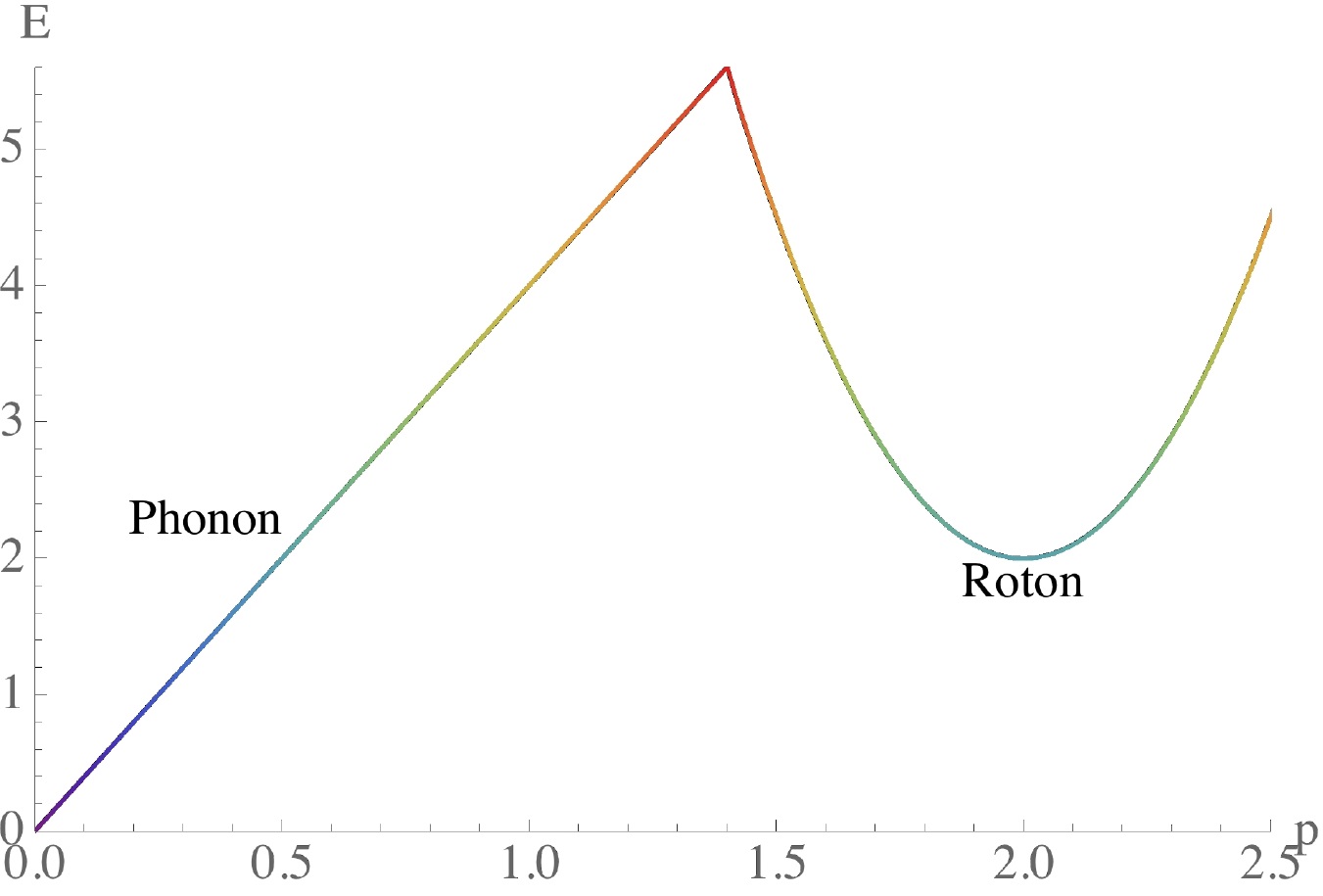
第二個結果雖然也涉及計算，但可以用簡單的光譜（圖3）來表示。若我們討論超流氦中的激發態，在低能量的區域（原點附近）我們可以看到一些聲子（phonon），但在光譜的右側有一個凹陷處，這個激發態對應到我們講的旋子。而費曼提出一個波函數從微觀的角度來了解這個旋子。類似的波函數之後也被應用在量子霍爾效應的問題中，用以計算光譜中的「磁旋子」（magneticroton）

在 1955 年，費曼更提出，當我們旋轉超流體，系統的漩渦度（vorticity）在巨觀上也是量子化的。

簡言之，一如大家對於費曼的期待，他在超流體的問題上成功留下了名字。那在超導體上又是如何呢？

某種意義上，超導體跟超流體很相似：兩者都是巨觀可見的量子效應，超導電流在超導體中可以無阻抗的導通可類比於超流體氦在細管線中無阻礙的流動。在數學結構上，超導體問題跟量子電動力學相似：後者是電子與量子化的光波交互作用，前者是電子與量子化的聲波交互作用。

費曼是超流體的專家，同時以量子電動力學拿下諾貝爾獎，從上面的類比，要突破超導問題似乎十拿九穩。也無怪乎當 Bardeen 得知費曼也在研究超導體問題時，還趕忙聘了對量子電動力學為專長的 Cooper  加入團隊。

出人意表的是，最後搶先登上巔峰的是 BCS 理論，反觀費曼，根據他自己的說法 [6]，則是白費了數年光陰，一無所獲。

從事後諸葛的角度，今天我們明白費曼當初研究方法的盲點。超流體與量子電動力學，很多的性質都能依賴微擾計算，也就是在前文中我們所說的，給定節點 g 的數目，畫出所有可能的費曼圖然後加總起來。尤其在量子電動力學，微擾計算給出精確到十位數的結果。這卻也造成一種思考的死角，也就是讓人習慣從微擾計算、費曼規則來定義物理模型。而不巧的是，超導體最重要的物理量之一，基態與激發態之間的能量差，不能寫成類似 g 的泰勒級數，也就是說即便費曼已經掌握了關鍵的物理機制，然而因為計算方法的不適切，無論他考慮再多的費曼圖，加總再多的高階修正，都不可能得到這個物理量。

有心的讀者，可以嘗試閱讀參考文獻 [5]，從字裡行間大家其實可以想像費曼說話的語氣，以及他在當時對於超導現象的困惑，以至於他在結語時感嘆，理論物理學家的想像力還不夠。（但之後不久， BCS 三人組便累積了足夠的「想像力」，提出了留名青史的 BCS 模型。）

筆者之所以挑選了一個費曼失敗的例子，主要是想讓大家了解，即便是費曼這個程度的高手，也有挑戰失敗的問題，並且很大一部分的原因是因為過於信賴自己最拿手的工具。退至凡人的科學生活，失敗更是常態。

昔人遠矣，雖不能企，但心嚮往之。對於傾心科學研究的讀者，可能不再需要另一個費曼的成功案例或軼事。筆者希望這個故事，可從另一個面向讓大家窺見科學研究生活更真實、真切的面貌。

 

參考資料：
[1] R. Feynman, Phys. Rev. 91, 1291 (1953).
[2] R. Feynman, Phys. Rev. 91, 1301 (1953).
[3] R. Feynman, Phys. Rev. 94, 262 (1954).
[4] R. Feynman, Progress in Low Temp Physics, Vol. 1, Ch. 2 (1955)
[5] R. Feynman, Rev. Mod. Phys. 29, 2 (1957).
[6] D. Goodsetin, and J. Goodstein, Phys. perspect. 2 (2000) 30-47.

 

--延伸閱讀：
路徑積分與費曼圖（上）
路徑積分與費曼圖（下）

 

--
作者：蕭維翰，臺大物理系畢業後逃到芝加哥，吹風吹雪之餘，做研究讀博士班。可惜離開臺灣後無海可看，只能在密西根湖旁揀一方堤岸，偽裝成看海的人。科教中心特約寫手，從事科普文章寫作。